Time2Graph: Revisiting Time Series Modeling with Dynamic Shapelets
本文最后更新于:2 年前
Introduction
本文旨在提供一种可解释的高效的时间序列建模(表示学习)方法来更好地服务分类任务。Shapelet在时间序列分类任务上体现了良好的可解释性。不过传统的基于Shapelet的方法忽略了Shapelet在不同时间片段上的动态性,即整个时间维度上不同的时间片段可能适合用不同的Shapelet。作者基于此设计了动态的time-aware shapelet,并且定义了shapelet evolution graph来捕获Shapelet在时间维度上的动态变化。
Preliminaries
时间序列集合\(T=\{t_1,\cdots,t_{|T|}\}\)包含若干条时序数据\(t=\{x_1,\cdots,x_n\}\)。一个\(t\)的片段\(s\)是\(t\)的一个连续子序列。如果\(t\)能被切分成\(m\)个长度都为\(l\)的片段,那么我们就有\(t=\{\{x_{l*k+1},\cdots,x_{l*k+l}\},0\leq k\leq m-1\}\)。两个长度相等的片段之间距离很好度量,直接计算欧式距离即可,那么两个片段长度不相等的情况呢?这就需要对其(Alignment)的概念。
Definition 1 Alignment. 给定两个长度分别为\(l_i\)和\(l_j\)的序列\(s_i\)和\(s_j\),一个alignment \(a=(a_1,a_2)\)是一个满足以下条件的长度为\(p\)的下标序列: \[ 1\leq a_k(1)\leq\cdots\leq a_k(p)=l_k,\\ a_k(n+1)-a_k(n)\leq 1,\\ \text{for }k=i,j,\text{ and }1\leq n\leq p-1 \]
上述公式可能比较抽象,其实看了下图就不难理解:
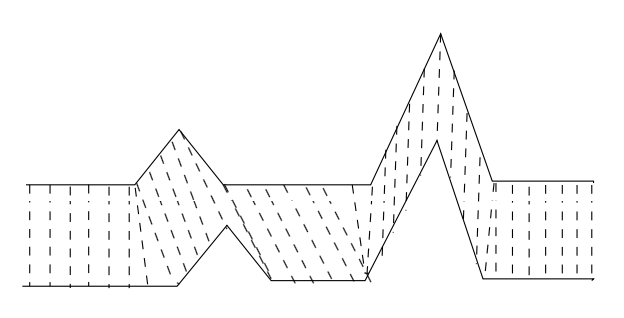
片段\(s_i\)中的某个点\(a\),与片段\(s_j\)中的某个点\(b\)形成对应,然后在\(a\)和\(b\)之间连一条虚拟的线(不能与已有的线交叉),一直这么做直到短的那个片段中的每个点都找到对应,就是一个合理的alignment。对于两个长度不一样的片段\(s_i\)和\(s_j\),会有很多种alignment。我们把\(s_i\)和\(s_j\)所有可能的alignment记为\(\mathcal{A}(s_i,s_j)\)。在定义了alignment之后就可以定义DTW了。DTW (Dynamic Time Warping) 定义为在给定一个预定义的距离度量\(\tau\)和所有可能的alignment \(\mathcal{A}(s_i,s_j)\)的情况下,最小的距离\(\tau\): \[ d_\text{DTW}(s_i,s_j)=\min_{a\in\mathcal{A}(s_i,s_j)}\tau(s_i,s_j|a) \]
进一步的,因为时间序列\(t\)也可以看作是一个片段,我们可以定义一个子序列\(s\)和时间序列\(t\)之间的距离度量: \[ D(s,t)=\min_{1\leq k\leq m} d(s,s_k) \]
这里\(\boldsymbol s_k\)为时序\(\boldsymbol t\)分解成的片段。之后Shapelet可以通过片段与时序的距离定义为最具有辨识度的有代表性的片段:
Definition 2 Shapelet. 一个Shapelet \(\boldsymbol v\)是对于特定类别时序的最具有代表性的片段。考虑时序分类任务,给定时序集合\(T\),可以通过与\(\boldsymbol v\)相似或不相似而分成两个子集合,与\(\boldsymbol v\)相似的集合与\(\boldsymbol v\)的距离应当尽量小,与\(\boldsymbol v\)不相似的集合与\(\boldsymbol v\)的距离应当尽量大,此时损失函数可以形式化为: \[ \mathcal L=-g(S_{pos}(\boldsymbol v,T),S_{neg}(\boldsymbol v,T)) \]
\(\mathcal L\)描述了在shapelet \(\boldsymbol v\)下正负样本集的相异性。\(S_{*}(\boldsymbol v,T)\)表示特定时序集合与\(\boldsymbol v\)的距离集合,\(g(\cdot,\cdot)\)为接受两个有限集合为输入的可微函数,并且能够度量两个集合的距离。
Framework
本文主要是提出了一种时间序列表示学习方法。基于Shapelet在不同的时间片段上的作用是不同的观察,作者为不同的时间片段赋予了不同的Shapelet,而不是像传统方法一样整个时序对应一个Shapelet。接着基于这些Shapelet作者构造了图,并通过图嵌入得到了嵌入向量,作为时序的表示。
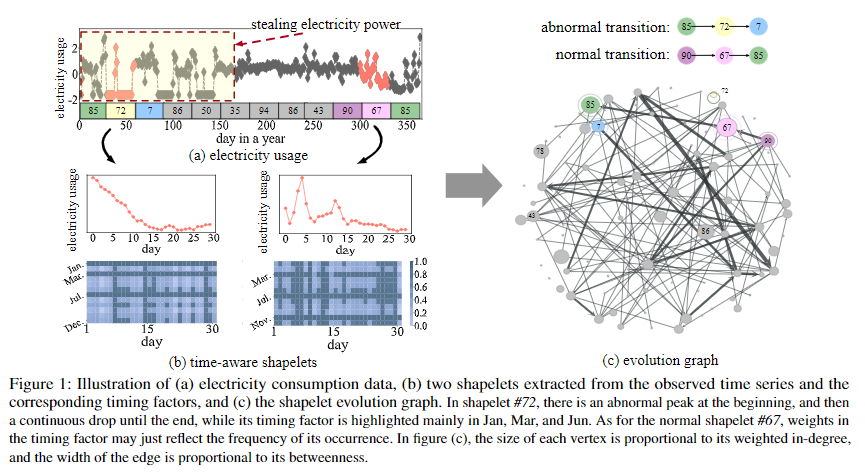
Time-Aware Shapelet Extraction
第一步是捕获Shapelet在时间维度上的动态影响。我们定义了两个参数来定量的测量shapelet在不同时间上的动态性。第一个是局部因子\(\boldsymbol w_n\),用来控制shapelet内部\(n\)个元素的权重,那么shapelet \(\boldsymbol v\)和片段\(\boldsymbol s\)的距离为: \[ \begin{align} \hat{d}(\boldsymbol v,\boldsymbol s|\boldsymbol w) &= \tau(\boldsymbol v,\boldsymbol s|\boldsymbol a^*,\boldsymbol w)\\ & = \left(\sum_{k=1}^{p}\boldsymbol w_{\boldsymbol a^*_1(k)}\cdot(\boldsymbol v_{\boldsymbol a^*_1(k)}-\boldsymbol s_{\boldsymbol a^*_2(k)})^2\right)^{\frac{1}{2}} \end{align} \] 其中\(\boldsymbol a^*\)为DTW距离下的最佳对齐。
第二个是全局因素\(\boldsymbol u_m\),这主要是通过对不同片段\(\boldsymbol s\)施加不同的权重实现的,于是shapelet \(\boldsymbol v\)和时间序列\(\boldsymbol t\)的距离可以重写为: \[ \hat{D}(\boldsymbol v,\boldsymbol t|\boldsymbol w,\boldsymbol u)=\min_{1\leq k\leq m}\boldsymbol u_k\cdot\hat{d}(\boldsymbol v,\boldsymbol s_k|\boldsymbol w) \] 其中\(\boldsymbol t\)被分割为\(m\)个片段:\(\boldsymbol t=\{\boldsymbol s_1,\cdots,\boldsymbol s_m\}\)。对于分类任务,具体的来说,我们先生成一堆Shapelet候选集,然后通过有监督的方法来挑选最佳的Shapelet和对应的参数\(\boldsymbol w\)和\(\boldsymbol u\)。
计算shapelet候选集的算法如下:

在获取了Shapelet候选集合之后,我们有带有标签的时序集合\(T\),对于每一个Shapelet我们可以优化:
\[ \hat{\mathcal L}=-g(S_{pos}(\boldsymbol v,T),S_{neg}(\boldsymbol v,T))+\lambda\parallel \boldsymbol w\parallel+\epsilon\parallel \boldsymbol u\parallel \]
来获取最优的\(\hat{\boldsymbol w}\)和\(\hat{\boldsymbol u}\)。然后,我们可以挑选出使得\(\hat{\mathcal L}\)最小的前\(K\)个Shapelet。整个过程的算法流程如下:

Shapelet Evolution Graph
在获取了Shapelet之后,为了捕获Shapelet之间的相关性,我们定义了Shapelet Evolution Graph。
Definition 3 Shapelet Evolution Graph. Shapelet Evolution Graph为一个有向带权图\(G=(V,E)\),\(V\)为\(K\)个Shapelet,每条带有权重\(w_{ij}\)的边\(e_{ij}\in E\)代表两个Shapelet \(\boldsymbol v_i \in V\)和\(\boldsymbol v_j \in V\)被分配给相邻片段的概率。
Graph Construction
这里来说一下,建图的具体过程。首先顶点为Shapelet,之后来进行边的构造。对于每一个片段\(\boldsymbol s_i\),我们会计算Shapelet到该片段的距离,距离越近代表这个Shapelet与片段越匹配。之后会设定一个阈值\(\delta\),然后将与片段的距离低于这个阈值的Shapelet分配给这个片段(一个Shapelet可能会分配给多个不同片段)。对于\(\boldsymbol s_i\)的所有shapetlet我们记为\(\boldsymbol v_{i,*}\),我们会按照Shape到片段的距离进行归一化:
\[ \boldsymbol p_{i,j}=\frac{\max(\hat{d}_{i,*}(\boldsymbol v_{i,*},\boldsymbol s_i))-\hat{d}_{i,j}(\boldsymbol v_{i,j},\boldsymbol s_i)}{\max(\hat{d}_{i,*}(\boldsymbol v_{i,*},\boldsymbol s_i))-\min(\hat{d}_{i,*}(\boldsymbol v_{i,*},\boldsymbol s_i))} \]
其中\(\hat{d}_{i,*}(\boldsymbol v_{i,*},\boldsymbol s_i)=\boldsymbol u_*[i]*\hat{d}(\boldsymbol v_{i,*},\boldsymbol s_i|\boldsymbol w_*)<\delta\)。这样对于每个片段\(\boldsymbol s_i\)所分配的Shapelet对应的\(\boldsymbol p\)之和会等于\(1\)。对每一对相邻的片段\((\boldsymbol s_i,\boldsymbol s_{i+1})\)的Shapelet \(\boldsymbol v_{i,j}\)和\(\boldsymbol v_{i+1,k}\),我们创建一条连接\(\boldsymbol v_{*,j}\)和\(\boldsymbol v_{*,k}\)的边\(e_{j,k}\),权重为\(\boldsymbol p_{i,j}\cdot\boldsymbol p_{i+1,k}\)。最后,所有重复的边会被合并。

如上图所示,假设有两个片段,每个片段分配了\(3\)个Shapelet,Shapelet \(B\)在片段\(1\)对应的概率是\(p_{12}\),Shapelet \(C\)在片段\(2\)对应的概率是\(p_{23}\),那么由于片段\(1\)和\(2\)是相邻片段,会在\(B\)和\(C\)之间连一条边,边的权重为\(p_{12}*p_{23}\)。
建图的算法流程图如下:

Representation Learning
之后,我们使用DeepWalk算法来获取获取每个结点(Shapelet)的嵌入表示。对于时序\(\boldsymbol t=\{\boldsymbol s_1,\cdots,\boldsymbol s_m\}\)即对应的Shapelet \(\{\boldsymbol v_{1,*},\cdots, v_{m,*}\}\)和对应的概率\(\{\boldsymbol p_{1,*},\cdots,\boldsymbol p_{m,*}\}\),每个Shaplet \(\boldsymbol v_{i,j}\)的表示记为\(\boldsymbol \mu(\boldsymbol v_{i,j})\)。片段\(\boldsymbol s_i\)对应的嵌入向量为对应的Shapelet嵌入向量与对应的概率值加权求和:
\[ \boldsymbol\Phi_i=\left(\sum_j p_{i,j}\cdot\boldsymbol \mu(\boldsymbol v_{i,j})\right),\space 1\leq i \leq m \]
算法流程如下:

Experiments
Experimental Setup
文中用了Earthquakes (EQS)、WormsTwoClass (WTC)、Strawberry (STB)、Electricity Consumption Records (ECR)和Network Traffic Flow (NTF) 这五个数据集,其中后两个为作者自己收集的数据集。五个数据集对应的统计信息如下:
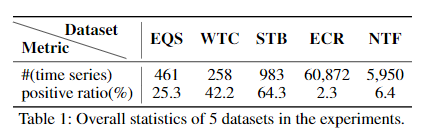
文中与多个Baseline进行了比较,包括:
- Distance-based Models: 文中使用了不同的距离度量与基于1-NN的模型进行组合,包括Euclidean Distance (ED)、Dynamic Time Warping (DTW)、Weighted DTW (WDTW)、Complexity-Invariant Distance (CID) 和 Derivative DTW (DDTW);
- Feature-based Models: 文中分别使用了提取特征(均值、标准差等)和原始序列来训练XGBoost。除此之外,还使用了 Bag-of-Patterns (BoP)、Time Series Forest (TSF)、Elastic Ensembles (EE) 和 基于SAX的 Vector Space Model (SAXVSM);
- Shapelet-based Models: 这部分模型包括 Learn Time Series Shapelets (LS)、Fast Shapelets (FS)、和 Learned Pattern Similarity (LPS);
- Deep Learning Models: 这部分模型包括MLP、LSTM和VAE。
Comparison Results
对于前三个公共数据集评测标准采用Accuracy,后两个数据集因为样本类比不均衡,所以采用了Precision、Recall和F1作为评测标准。结果如下:
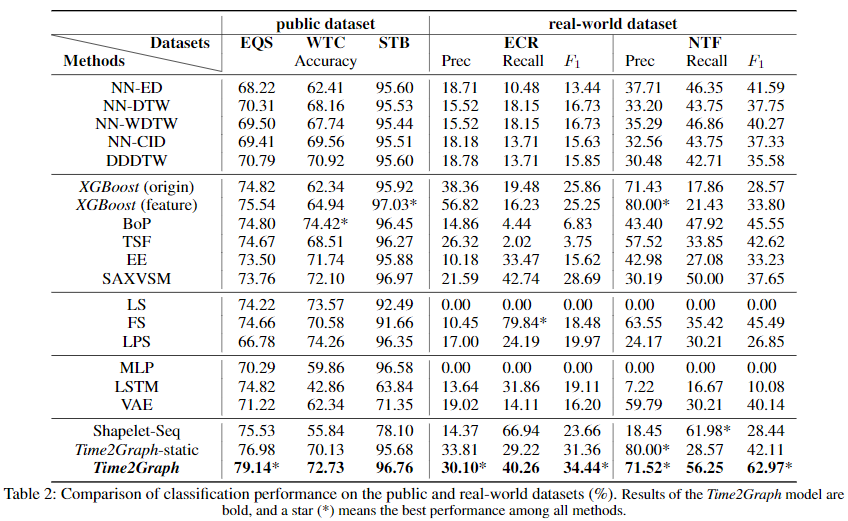
在EQS数据集上,Time2Graph打败了所有Baseline,而在WTC和STB这两个数据集上也达到了较好的效果。在ECR和NTF这两个真实数据集上,Time2Graph在F1上打败了所有Baseline。
Parameter Analysis
本节对Shapelet的数量\(K\)、嵌入维度\(B\)和片段长度\(l\)进行了参数分析。结果如下:
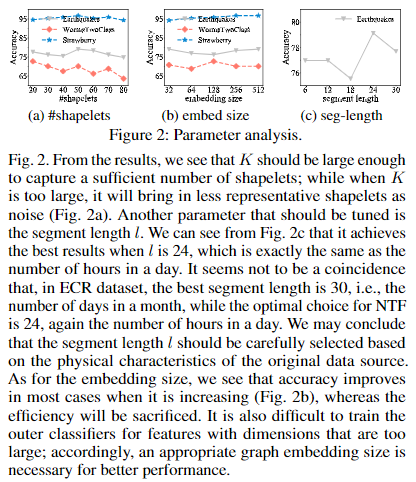
Case Study of Time-Aware Shapelets
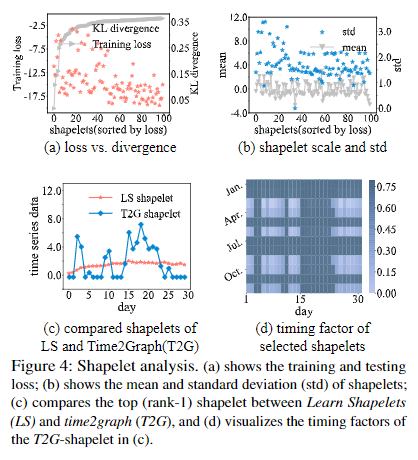
本节作者对提出的Time-Aware Shapetlet进行了细致的探究。第一个问题是不同Shapelet的区分能力是否不同?下图(a)里,作者在使用Shapelet进行二分类的任务中,将Shapelet按Loss(图中灰色的线)进行排序,并且绘制了对应的正负样本距离的KL散度(橘红色的点)。可以看到,在Loss曲线和KL散度呈反比关系。KL散度越高,我们可以认为该Shapelet的区分度越高,这说明不同Shapelet的区分度的确不同,并且这会与最终效果直接挂钩。图(b)展示了不同Shapelet的均值和方差(原文没有说清楚是什么的均值和方差)。
除此之外,作者和流行的Shapelet提取算法LS进行了比较,如图(c)和图(d)。从图中可以看到对于不同时间,本文的算法提取的Shapelet的确是具有时间动态性的。
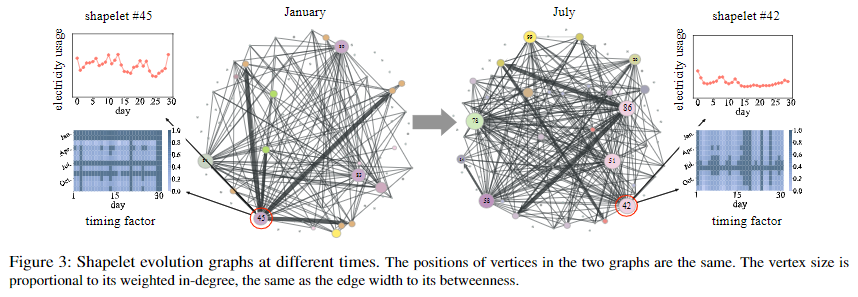
Case Study of the Shapelet Evolution Graph
本节作者对Shapelet Evolution Graph进行了细致的探究。下图分别为一月份和七月份的Shapelet Evolution Graph。在一月,45号Shapelet的度较大,而且对应的时间因素在一月和二月也较大(图中深色部分)。说明45号Shapelet在一月份具有代表性。而在七月,45号Shapelet的重要性降低,而42号Shapelet在七月的重要性很高。
本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!