Classification-based Anomaly Detection for General Data

Introduction

本文主要是对NIPS18这篇异常检测文章的改进，首先是利用了标签信息来提升算法的表现，其次是将算法扩展到了非图像数据。作者对现有的异常检测算法进行了回顾：

• Reconstruction Methods： 这一部分方法假设异常样本和正常样本能够通过重构任务来进行区分。通过在正常样本上学习重构任务，之后对于正常样本，模型能够很好地进行重构，而异常样本则会有较高的重构误差。
• Distributional Methods： 这一部分方法将异常检测看作是密度估计问题。通过对正常样本的分布进行估计，异常样本在该正常分布下的似然将会很低。
• Classification-based Methods： 这一部分方法主要是指的单分类方法和通过几何变换构造分类任务的方法。本文使用的就是这类方法。

Proposed Method

Classification-based Anomaly Detection

假设所有数据位于空间\(R^L\)内，而正常数据位于子空间\(X\subset R^L\)内。我们假设所有的异常样本位于\(X\)之外。为了检测异常，我们希望学习一个分类器\(C\)使得对于所有的\(x\in X\)有\(C(x)=1\)，而对所有的\(x\in R^L\backslash X\)有\(C(x)=0\)。

单分类方法的思想是直接学习\(P(x\in X)\)，代表的方法有One-Class SVM，DSVDD等。传统的OC-SVM直接在原始空间或者核空间学习分类器。比较新的方法，如Deep-SVDD则是先将样本转换到一个特征空间，然后在这个特征空间上学习使得半径\(R\)最小的超球体（球心\(c_0\)），来覆盖住所有正常样本。异常的判定则通过计算\(\parallel f(x)-c_0\parallel^2-R^2\)来实现。不过学习一个好的样本到特征空间的变换并不是一件容易的事情，比如说\(f(x)=0, \forall x \in X\)就是一个使得超球体最小的解。所以需要很多trick来避免诸如此类的情况。

Geometric-transformation classification (GEOM) 则将数据空间\(X\)通过\(M\)个几何变换转换到一系列子空间\(X_1,\cdots,X_M\)。之后训练一个分类器来预测样本\(T(x,m)\)对应的几何变换的种类\(m\)。转换后的正常图片空间记为\(\cup_m X_m\)，所以该方法尝试估计以下条件概率： \[ P(m^\prime|T(x,m))=\frac{P(T(x,m)\in X_{m^\prime})P(m^\prime)}{\sum_{\bar{m}}P(T(x,m)\in X_{\bar{m}})P(\tilde{m})}-\frac{P(T(x,m)\in X_{m^\prime})}{\sum_{\bar{m}}P(T(x,m)\in X_{\bar{m}})} \]

对于异常的样本\(x\in R^L\backslash X\)，在经过几何变换之后，都不会位于正确的子空间中，即\(T(x,m)\in R^L\backslash X_m\)。之后，使用\(P(m|T(x,m))\)来判定异常。

作者认为，这种方法的问题是分类器\(P(m^\prime|T(x,m))\)只在正常数据上训练，而对于异常样本的异常分数会出现方差很大的问题。

一种解决方式是加入异常样本进行训练，但是作者认为在有的任务中标签很难获取，于是作者使用了另外一种方法来解决这个问题。

Distance-based Multiple Transformation Classification

和GEOM一样，先对每个样本进行\(M\)个几何变换，然后学习一个特征提取器\(f(x)\)，将\(X_m\)映射到特征空间。之后和OC-SVM类似，假设特征\(\{f(x)|x\in X_m\}\)为球心为\(c_m=\frac{1}{N}\sum_{x\in X} f(T(x,m))\)的超球体。样本属于某一类\(m^\prime\)的概率由下式给出：

\[ P(m^\prime|T(x,m))=\frac{e^{-\parallel f(T(x,m))-c_{m^\prime}\parallel^2}}{\sum_{\bar m}e^{-\parallel f(T(x,m))-c_{\bar m}\parallel^2}} \]

目标函数采用的是Triplet Loss：

\[ L=\sum_i\max(\parallel f(T(x_i,m))-c_m\parallel^2+s-\min_{m^\prime\neq m}\parallel f(T(x_i,m))-c_{m^\prime}\parallel^2,0) \]

\(\parallel f(T(x_i,m))-c_m\parallel^2\)相当于最小化了类内距离，\(\min_{m^\prime\neq m}\parallel f(T(x_i,m))-c_{m^\prime}\parallel^2\)最大化了每个类对应的集簇间距离。在检测阶段，为了避免一些数值问题，作者做了一些平滑操作：

\[ \tilde P(m^\prime|T(x,m))=\frac{e^{-\parallel f(T(x,m))-c_{m^\prime}\parallel^2+\epsilon}}{\sum_{\tilde m}e^{-\parallel f(T(x,m))-c_{\tilde m}\parallel^2+M\cdot\epsilon}} \]

最后的评判分数由下式给出：

\[ Score(x)=-\log P(x\in X)=-\sum_m\log \tilde{P}(T(x,m)\in X_m)=-\sum_m\log\tilde{P}(m|T(x,m)) \]

算法流程图如下：

Parameterizing the Set of Transformations

在GEOM中，由于使用的几何变换都是针对图像的，所以对于其他类型的数据并不适用。本文中作者对非图像数据设计了以下变换：

\[ T(x,m)=W_mx+b_m \]

不同的参数\(W_m\)和\(b_m\)即为不同的几何变换，可以考虑采用随机采样的方式。

Experiments

Image Experiments

对于图像数据的异常检测实验，作者采用了CIFAR10、FasionMNIST这两个数据集，实验结果如下：

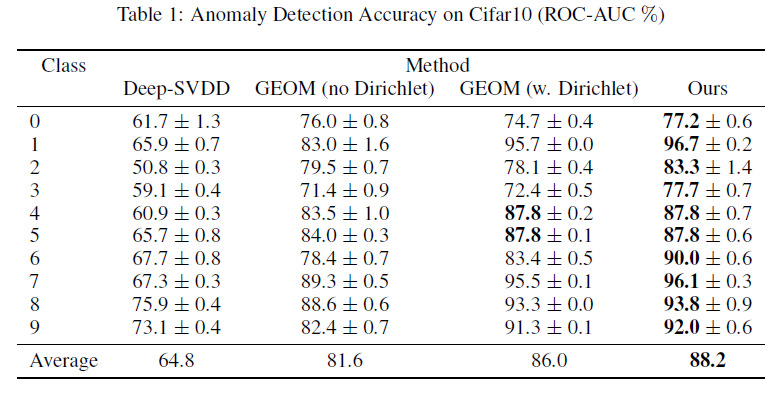
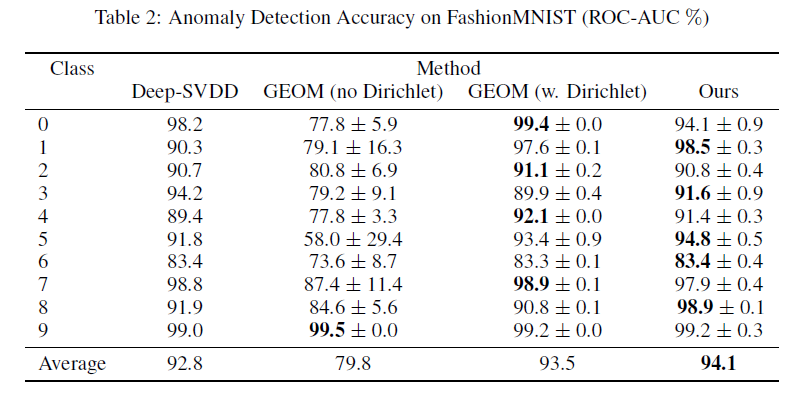
Tabular Data Experiments

对于非图像数据，作者采用了几个小的数据集：Arrhythmia、Thyroid、KDD和KDDRev。采用的Baseline包括OC-SVM、E2E-AE、LOF、DAGMM和FB-AE (Feature Bagging Autoencoder)。对于几何变换的参数，采样自标准正态分布。结果如下：

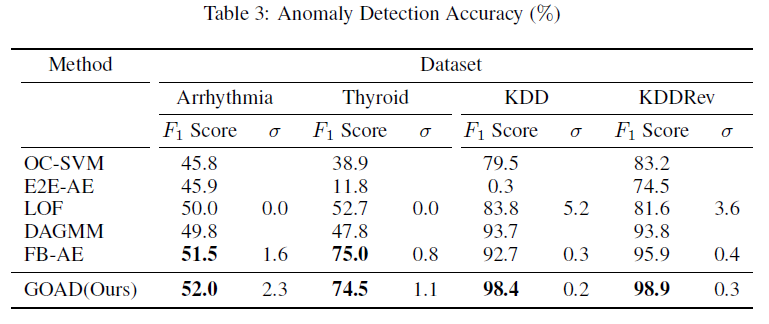
Remark

结合OpenReview上的一些讨论，这里提出一些问题和总结：

• KDD数据集太简单了，正常、异常样本能够很容易被分开；
• 对于图像数据作者只使用了CIFAR10和FashionMNIST这两个比较小的数据集，而在GEOM中还使用了CIFAR100和CatsVsDogs。并且GEOM原文中提到数据集（指图像大小）越大，GEOM的优势就越明显，所以在本文的实验中只使用这两个数据集说服力略显不够；
• 关于评测标准的问题，作者在图像数据中用的是AUROC，而非图像数据用的是F1 score。像AUPR、AUROC这种评测标准往往更加全面，而F1 score依赖于阈值的选取。如果是遍历阈值找到最好的那个F1 score，则无法全面考察模型的鲁棒性，模型有可能只是在特定的阈值下表现很好，而阈值稍微偏差一下性能可能就会大幅下降。我看到的大多数异常检测文章都是使用AUROC或者F1加上AUROC作为评测指标；
• 文中在第二节“CLASSIFICATION-BASED ANOMALY DETECTION”的末尾两段关于GEOM方法的缺点说的很模糊。异常分数的方差大到底指的是什么；
• 关于作者提出的变换\(T(x,m)=W_mx+b_m\)并没有用到图像数据的实验上，而且在实验中\(b_m\)这个参数实际上是被忽略掉了的，\(b_m\)的作用究竟如何不得而知。而且GEOM中的几何变换的Motivation在原文中是做了实验充分讨论了的，GEOM的作者认为这些几何变换保留了图像的高阶语义信息。而本文中的变换中的参数只是随机采样而来，并不存在说保留原始数据中的结构信息。如果忽略掉这一层变换，那就类似于加了神经网络提取特征的OC-SVM。