Unsupervised Feature Learning via Non-Parametric Instance Discrimination
本文最后更新于:2 个月前
Introduction
本文基于样本分类和噪声对比估计提出了一个无监督表示学习算法。下图展示了一个Intuition Example:

对于一个有监督的分类器,输入一张图片,作者观察到分类器的Softmax Response中较高的那些类都是在视觉上看起来比较接近的(美洲豹Leopard,美洲虎Jaguar,印度豹Cheetah),也就是说网络捕捉到了类间的视觉相似性,不过这是在有标签的情况下。对于无监督表示学习任务,作者将这个观察推广到了一个极端情况,就是把每一个样本都视作不同的类,然后让分类器来学习样本(类)间的视觉相似性。不过直接这么做会有严重的效率问题,所以作者还利用了Memory Bank机制和噪声对比估计来提高效率。
Proposed Method
学习一个嵌入表示函数\(\mathbf v=f_\theta(x)\)。在表示空间中\(d_\theta(x,y)=\parallel f_\theta(x)-f_\theta(y)\parallel\)
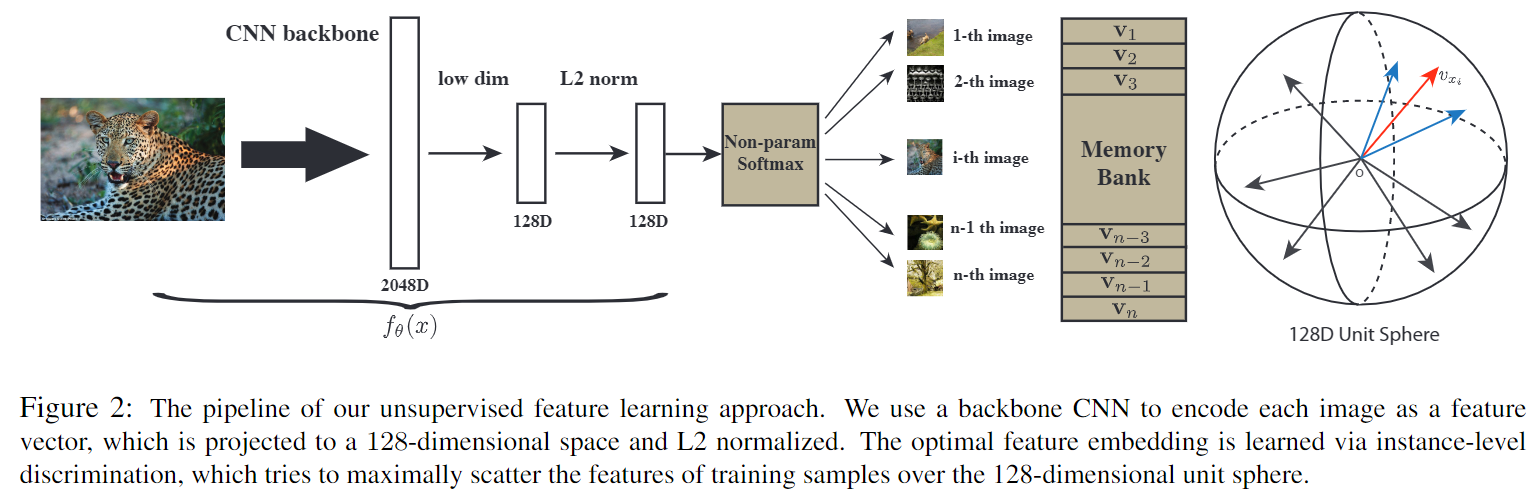
Non-Parametric Softmax Classifier
Parametric Classifier
在经过嵌入表示函数之后,得到表示向量\(\mathbf v_i=f_\theta(\mathbf x_i)\)。要基于这个向量进行分类, \[ P(i|\mathbf v)=\frac{\exp(\mathbf w_i^\top\mathbf v)}{\sum_j\exp(\mathbf w_j^\top\mathbf v)} \]
Non-Parametric Classifier
\[ P(i|\mathbf v)=\frac{\exp(\mathbf v_i^\top\mathbf v/\tau)}{\sum_j\exp(\mathbf v_j^\top\mathbf v/\tau)} \]
同时约束\(\parallel \mathbf v\parallel=1\)
最后的损失函数为负对数似然损失(negative log-likelihood): \[ J(\theta)=-\sum_{i=1}^n\log P(i|f_\theta(x_i)) \]
到这里,算法的大框架就确定下来了,剩下的就是解决两个效率上的问题。一个是损失函数的计算每次都需要计算整个训练集的表示,同时Softmax函数由于分母对应的项目很多(等于训练集大小)在效率上也有问题。
Learning with A Memory Bank
这里解决第一个效率问题。要计算损失函数,需要遍历整个训练集获得对应的表示,而在训练的时候是一批一批的数据,每次重新计算表示效率很低。为了解决这个问题,作者引入了缓存机制,即加入一个memory bank \(V\),用来保存计算好的表示\(\mathbf f_i=f_\theta(x_i)\)。一开始\(V\)采用单位随机向量初始化,之后在训练的时候不断更新\(\mathbf f_i\rightarrow \mathbf v_i\)。
Noise Contrastive Estimation
第二个效率问题很容易想到使用噪声对比估计(Noise Contrastive Estimation, NCE)来做。NCE主要是将计算复杂的分母作为一个参数来进行优化: \[ P(i|\mathbf v)=\frac{\exp(\mathbf v^\top\mathbf f_i/\tau)}{Z_i} \]
其中\(Z_i=\sum_{j=1}^n\exp(\mathbf v^\top_j\mathbf f_i/\tau)\),噪声分布\(P_n=1/n\),如果噪声样本数量是真实数据的\(m\)倍,那么随意给定一个样本,其属于真实样本的后验概率为: \[ h(i,\mathbf v)=P(D=1|i,\mathbf v)=\frac{P(i|\mathbf v)}{P(i|\mathbf v)+mP_n(i)}=\sigma\left(s(\mathbf v)-\log \{m P_n(i)\}\right) \] 其中\(\Delta s=s(\mathbf v)-\log [m P_n(i)]\)。这里的真实数据分布\(P_d\)为。NCE的损失函数就是要最大化\(h(i,\mathbf v)\),最小化\(h(i,\mathbf v^\prime)\) \[ J_{NCE}(\theta)=-E_{P_d}[\log h(i,\mathbf v)]-m\cdot E_{P_n}[\log(1-h(i,\mathbf v^\prime))] \] 为了计算\(Z_i\) \[ Z\simeq Z_i\simeq nE_j[\exp(\mathbf v_j^\top\mathbf f_i/\tau)]=\frac{n}{m}\sum_{k=1}^m\exp(\mathbf v_{j_k}^\top\mathbf f_i/\tau) \]
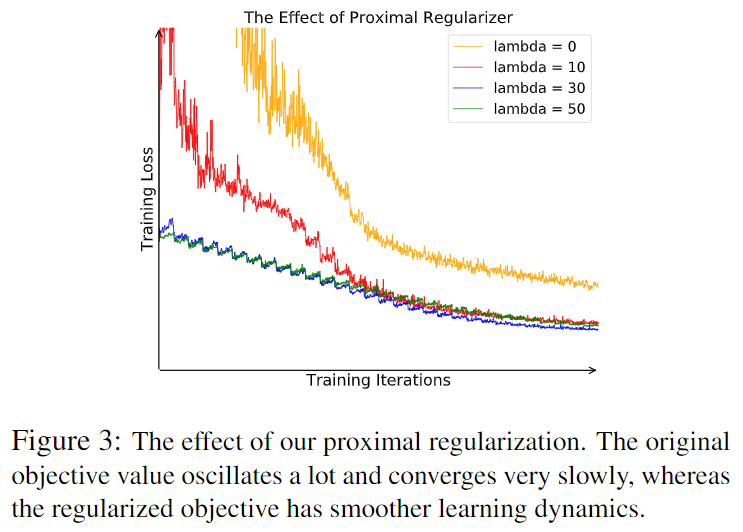
Proximal Regularization
每个类别只有一个样本 \[ -\log h(i,\mathbf v_i^{(t-1)})+\lambda\parallel\mathbf v_i^{(i)}-\mathbf v_i^{(i-1)}\parallel^2_2 \]
最终的损失函数:
\[ J_{NCE}(\theta)=-E_{P_d}\left[\log h(i,\mathbf v_i^{(t-1)})-\lambda\parallel\mathbf v_i^{(t)}-\mathbf v_i^{(t-1)}\parallel^2_2\right]\\ -m\cdot E_{P_n}\left[\log(1-h(i,\mathbf v^{\prime(t-1)}))\right] \]
Weighted k-Nearest Neighbor Classifier
\(s_i=\cos(\mathbf v_i,\hat{\mathbf f})\)。记\(\mathcal N_k\)。\(w_c=\sum_{i\in\mathcal N_k}\alpha_i\cdot 1(c_i=c)\)。
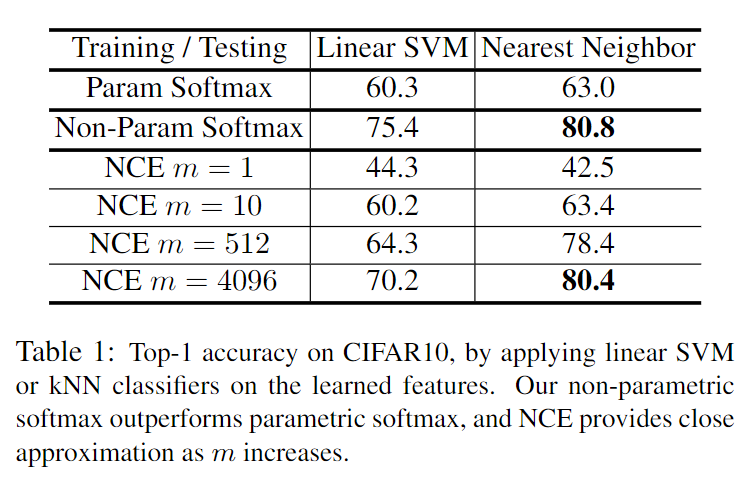
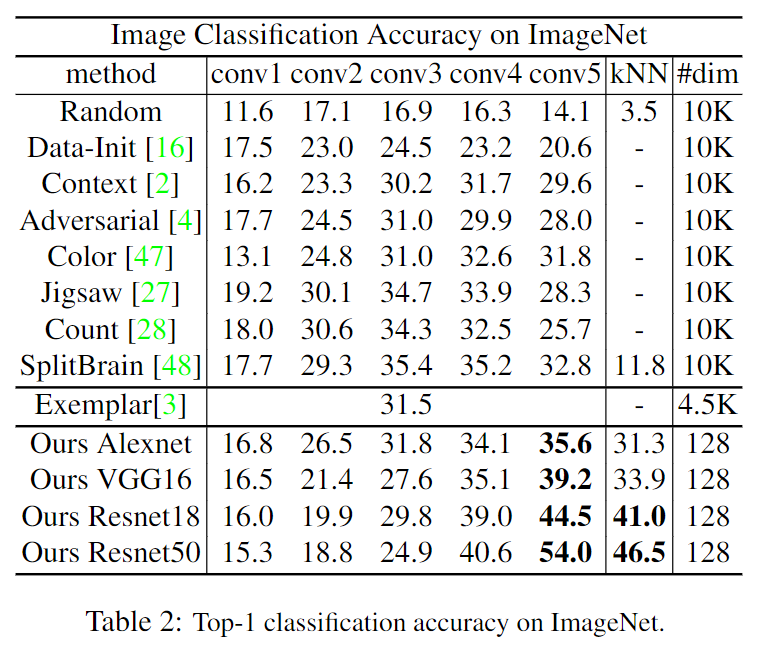
Experiments
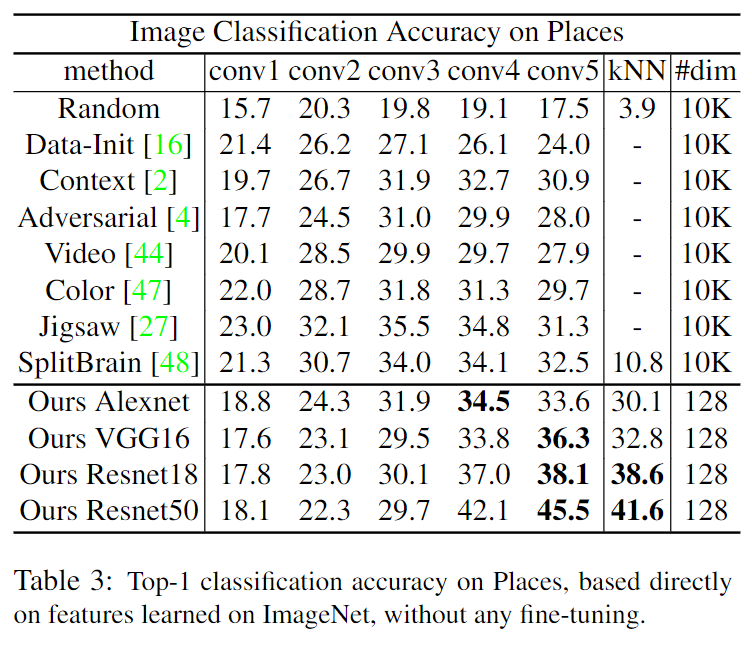


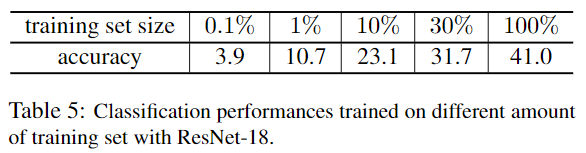
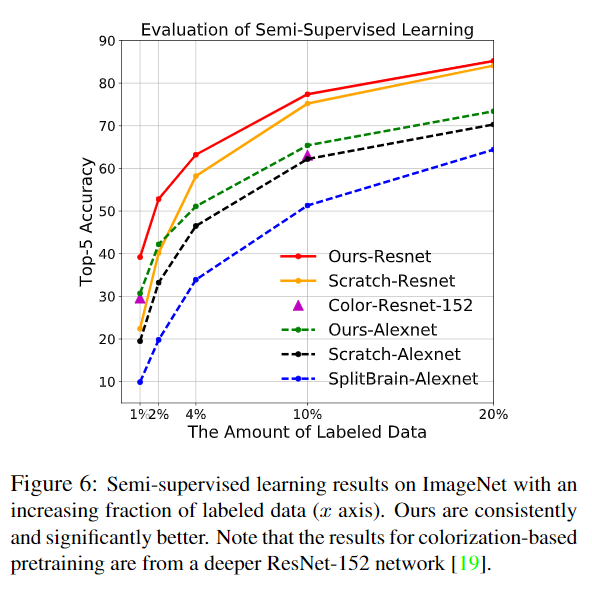
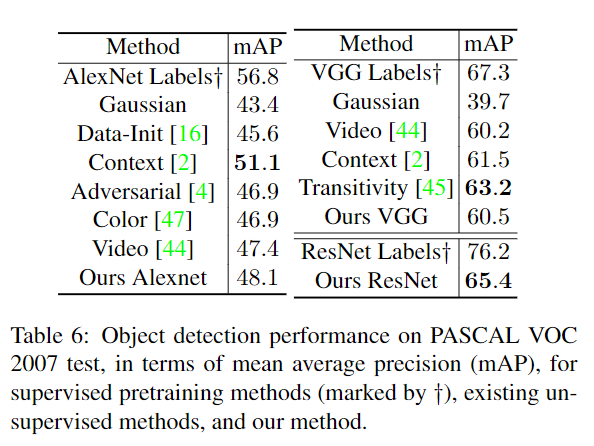
本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!