Representation Learning with Contrastive Predictive Coding
本文最后更新于:1 年前
Introduction
这篇文章算是Contrastive Learning的开山之作之一了,本文提出了表示学习框架:Contrastive Predictive Coding(CPC)和InfoNCE Loss。
Proposed Method
Contrastive Predictive Coding
N-pair Loss: \[ \mathcal L=-\log\frac{\exp(f^+\cdot f^\top)}{\exp(f^+\cdot f^\top)+\sum_{f_j\neq f^\top}\exp(f^+\cdot f_j)} \] 你有N个样本\(\{x_1,x_2,\cdots,x_N\}\),然后对应的表示为\(f_j\)。假设当前样本为\(f^+\),在所有的\(f_j\)中只有一个表示与\(f^+\) match,记为\(f^\top\)(可以理解为属于同一类,或者两个相似),其他的都是负样本。我们优化上面的优化公式就会拉近\(f^+\)和\(f^\top\)之间的距离(拉近同类),疏远\(f^+\)和所有其他负样本\(f_j\)的距离(疏远异类)。不过在N-pair Loss中,正负样本是根据标签来选取的,然而在这里我们没有标签。
下图展示了Contrastive Predictive Coding的结构:
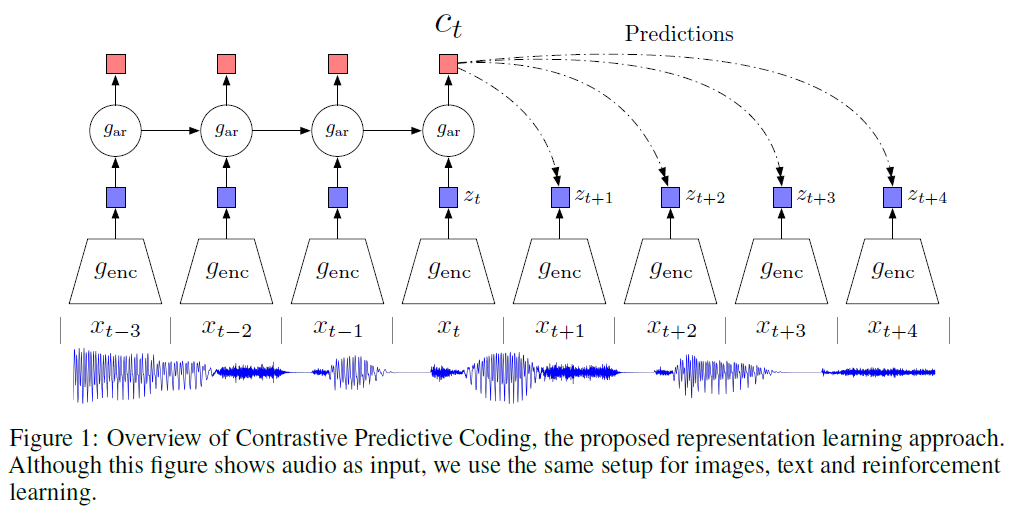
对比学习 \[ \mathcal L(f_i)=-\log\frac{\exp(f_i\cdot f^\top)}{\sum_j\exp(f_i\cdot f_j)} \] 设数据集(一个Batch)为\(\mathbf X=\{x_1,x_2,\cdots,x_N\}\),正样本对为,负样本对。
至于\(f(\cdot,\cdot)\)的具体形式,其实\(\frac{p(x_{t+k}|c_t)}{p(x_{t+k})}\)这个式子我们也是没法直接优化的,因为这个Density Ratio无法直接算出来。在这里,作者使用了一个替代的办法,就是用\(\mathbf c_t\)来预测未来的隐变量\(\hat{\mathbf z}_{t+1},\hat{\mathbf z}_{t+2},\cdots\),而真实的隐变量\(\mathbf z_{t+1},\mathbf z_{t+2},\cdots\)我们是知道的。这里预测直接使用权重矩阵和\(\mathbf c_t\)相乘: \[ f_k(\mathbf x_{t+k},\mathbf c_t)=\exp\left(\mathbf z_{t+k}^T \cdot \mathbf W_k\mathbf c_t\right) \]
上式有点难以理解,实际上预测值\(\hat{\mathbf z}_{t+k}=\mathbf W_k\mathbf c_t\),而\(\mathbf z_{t+k}\hat{\mathbf z}_{t+k}\)相当于计算两者的距离,即相似性。所以\(f_k(\cdot,\cdot)\)其实是在计算预测值和真实值的相似性。现在大家先接受这个\(f(\cdot,\cdot)\)的定义,因为后面会证明优化这个\(f(\cdot,\cdot)\)就相当于在优化Density Ratio \(\frac{p(x_{t+k}|c_t)}{p(x_{t+k})}\)。
一个来自\(p(x_{t+k}|c_t)\)的正例和\(N-1\)个来自\(p(x_{t+k})\)的负例,目标函数(文中称为CPC Loss)为: \[ \mathcal L_N=-\mathop{\mathbb E}\limits_X\left[\log\frac{f_k(x_{t+k},c_t)}{\sum_{x_j\in X}f_k(x_j,c_t)}\right] \]
这里相当于做了个\(N\)分类,因为这里损失函数等价于\(N\)分类交叉熵损失函数。
两个离散随机变量的交叉熵的定义为: \[ H(p,q) = -\sum_{x\in\mathcal X}p(x)\log q(x) \] 对于交叉熵损失函数,设\(i\)为真实标签,\(\hat{\boldsymbol y}\)为分类器的输出。\(\frac{\exp(\hat y_i)}{\sum_j\exp(\hat y_j)}\)为经过
Softmax归一化之后的输出,其每个分量\(\hat y_j\)相当于输入样本\(x\)的预测类别为\(j\)的概率。不过由于对于真实标签\(y\)来说,只有\(y_i=1\),其他的分量都为\(0\),所以最后交叉熵只剩下一项: \[ \mathcal L=-\log\left(\frac{\exp(\hat y_i)}{\sum_j\exp(\hat y_j)}\right) \]
\[ I(x;c)=\sum_{x,c}p(x,c)\log\frac{p(x|c)}{p(x)} \]
编码器\(g_{enc}\)将观测值\(\boldsymbol x_t\)编码到隐变量\(\boldsymbol z_t=g_\text{enc}(\boldsymbol x_t)\)(对应于局部信息),之后自回归模型\(g_{ar}\)将所有\(t\)之前的(包括\(t\))隐变量\(z_{\leq t}\)压缩到一个上下文隐变量\(\boldsymbol c_t=g_\text{ar}(\boldsymbol z_{\leq t})\)(希望具有预测性质,捕获了长时依赖性)。不过本文并不是基于\(\boldsymbol c_t\)来预测未来的观测值\(\boldsymbol x_{t+k}\),即估计分布\(p_k(\boldsymbol x_{t+k}|\boldsymbol c_t)\),而这样的话又要用到MSE之类的Loss。文中利用的是最大化\(\boldsymbol c_t\)和\(\boldsymbol x_{t+k}\)之间的互信息\(\log \frac{p(x_{t+k}|c_t)}{p(x_{t+k})}\)(这种形式的互信息被称为是点互信息,详见维基)。定义一个度量函数\(f(\cdot,\cdot)\),要求其具有与\(\frac{p(x_{t+k}|c_t)}{p(x_{t+k})}\)成比例的性质: \[ f_k(x_{t+k},c_t)\propto\frac{p(x_{t+k}|c_t)}{p(x_{t+k})} \] 这时最大化\(f(\cdot,\cdot)\)就相当于最大化两者的互信息。
Mutual Information Estimation Explanation
现在回到公式\(I(x;c)=\sum_{x,c}p(x,c)\log\frac{p(x|c)}{p(x)}\),
Multual Information
互信息是衡量已知一个变量时,另一个变量不确定性的减少程度的度量。对于离散随机变量,互信息的定义为: \[ I(X,Y)=\sum_{y\in\mathcal Y}\sum_{x\in\mathcal X}p(x,y)\log\frac{p(x,y)}{p(x)p(y)}=\sum_{y\in\mathcal Y}\sum_{x\in\mathcal X}p(x,y)\log\frac{p(y|x)}{p(y)} \] 对于连续随机变量,互信息的定义为: \[ I(X,Y)=\int_{\mathcal Y}\int_{\mathcal X}p(x,y)\log\frac{p(x,y)}{p(x)p(y)}\mathrm dx\mathrm d y=\int_{\mathcal Y}\int_{\mathcal X}p(x,y)\log\frac{p(y|x)}{p(y)}\mathrm dx\mathrm d y \] 互信息与熵之间的关系: \[ \begin{align} I(X,Y)&=H(X)-H(X|Y)\\ &=H(Y)-H(Y|X)\\ &=H(X)+H(Y)-H(X,Y)\\ &=H(X,Y)-H(X|Y)-H(Y|X) \end{align} \] 互信息与KL散之间的关系: \[ I(X,Y)=\mathbb E_Y[D_{KL}(p(x|y)\parallel p(x))] \] 从图中可以很容易看出互信息相当于\(X\)和\(Y\)两者的熵的“重叠”的部分:
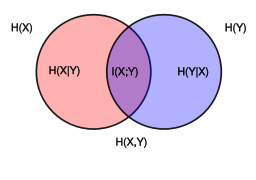
在表示学习中,互信息的应用越来越广泛。对于输入的数据\(X\),表示学习的目的是尽可能学到“好“的表示\(Z\),保留原始数据尽可能多的重要信息。如果使用基于重构的模型,我们就会要求最小化重构误差\(\parallel X-\hat{X}\parallel^2_2\),但是这种”逐像素“式的损失函数过于严苛,不利于模型学习高层语义信息。如果加入一个判别器来自动学习一个度量,首先增大了计算开销,同时GAN本身也有诸多问题。
现阶段很多工作使用互信息来判定学到的表示\(Z\)的好坏,即最大化原始数据\(X\)与表示\(Z\)之间的互信息: \[ Z^*=\mathop{\arg\max}_{p(z|x)}I(X,Z) \] 互信息越大意味着\(\log\frac{p(z|x)}{p(z)}\)越大,即\(p(z|x)\)要大于\(p(z)\)。\(p(z)\)可以看作是\(Z\)的先验,而\(p(z|x)\gg p(z)\)可以理解为在得知输入\(X\)之后,我们能找到专属\(X\)的那个编码\(Z\)。
接下来作者证明优化\(\mathcal L_N\)会使得\(f_k(\mathbf x_{t+k},\mathbf c_t)\)和互信息接近。这里的\(p(\mathbf x_{t+k}|\mathbf c_t)\)。设\(p(d=i|X,c_t)\)为给定数据集(或者Batch)\(X\)和context向量\(c_t\)的条件下,样本\(x_i\)为正样本的概率,有: \[ \begin{align} p(d=i|X,c_t)&=\frac{p(x_i|c_t)\prod_{l\neq i}p(x_l)}{\sum^N_{j=1} p(x_j|c_t)\prod_{l\neq j}p(x_l)}\\ &=\frac{\frac{p(x_i|c_t)}{p(x_i)}}{\sum^N_{j=1}\frac{p(x_j|c_t)}{p(x_j)}} \end{align} \]
$$ \[\begin{align} \mathcal L_\text{N}^\text{opt}&=-\mathop{\mathbb E}\limits_X\log\left[\frac{\frac{p(x_{t+k}|c_t)}{p(x_{t+k})}}{\frac{p(x_{t+k}|c_t)}{p(x_{t+k})}+\sum_{x_j\in X_\text{neg}}\frac{p(x_j|c_t)}{x_j}}\right]\\ \end{align}\] $$
\[ I(x_{t+k},c_t)\geq \log(N)-\mathcal L_N \]
可以说\(\mathcal L_N\)作为互信息\(I(x_{t+k},c_t)\)的一个下界。
Implementation Details
Experiments
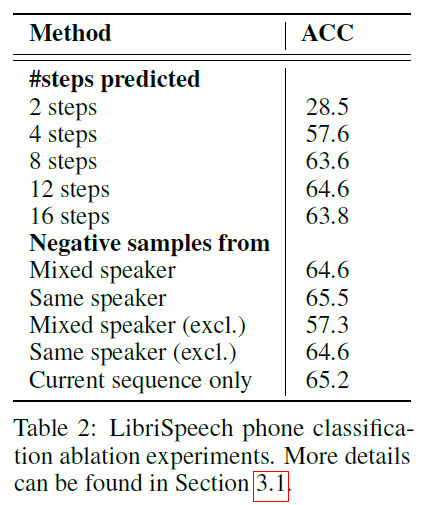
Audio

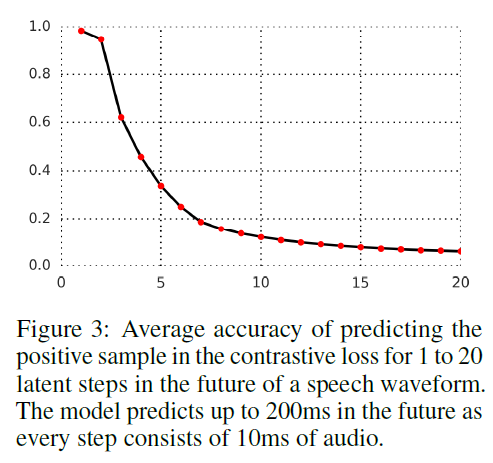
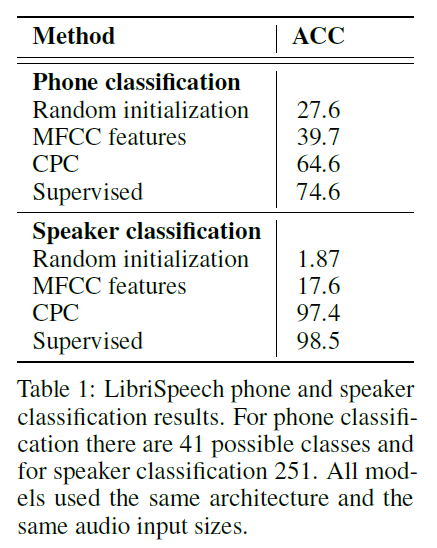
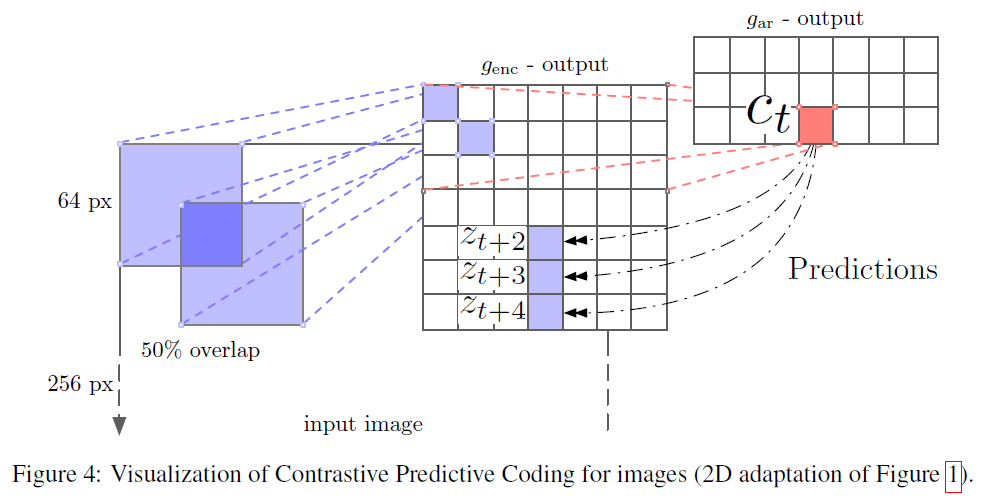
Vision


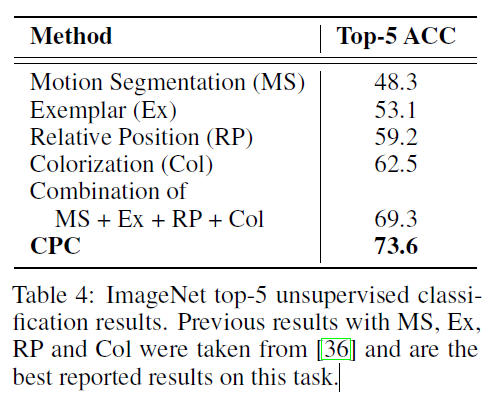
Natural Language

Reinforcement Learning
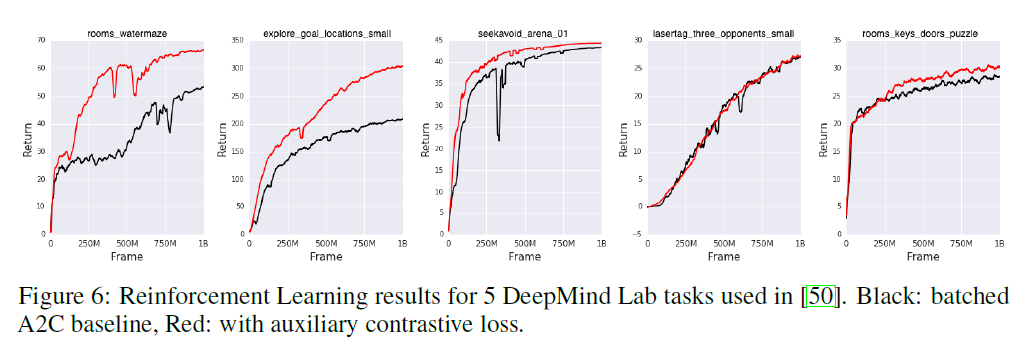
本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!