Machine Learning Ensemble Algorithms: GBDT and XGBoost
本文最后更新于:1 年前
Introduction
本文主要介绍GBDT和XGBoost,在学习本文内容之前建议先学习决策树相关内容。
下面是一些有用的参考链接:
Preliminaries
实际上,GBDT和梯度下降、XGBoost和牛顿法之间是存在密切关系的,这里我们先回顾一下梯度下降算法和牛顿法的基础知识。
Taylor Formulation
函数\(f(x)\)在点\(x_0\)处的泰勒展开为: \[ f(x)=\sum_{n=0}^\infty\frac{f^{(n)}(x_0)}{n!}(x-x_0)^n \] 特别的,一阶展开为: \[ f(x)\approx f(x_0)+f^\prime(x_0)(x-x_0) \] 二阶展开为: \[ f(x)\approx f(x_0)+f^\prime(x_0)(x-x_0) + f^{\prime\prime}(x_0)\frac{(x-x_0)^2}{2} \] 迭代形式:假设\(x^t=x^{t-1}+\Delta x\),将\(f(x)\)在\(x^{t-1}\)处进行泰勒展开 \[ \begin{align} f(x^t) &= f(x^{t-1}+\Delta x)\\ &\approx f(x^{t-1})+f^\prime(x^{t-1})\Delta x + f^{\prime\prime}(x^{t-1})\frac{\Delta x^2}{2} \end{align} \]
Gradient Descend Method
设参数\(\theta\),那么参数对应的损失函数为\(L(\theta)\),
设当前步数为\(t\),那么\(t-1\)步时的参数为\(\theta^{t-1}\),将\(L(\theta^t)\)在\(\theta^{t-1}\)处展开得到:
\[ L(\theta^t) \approx L(\theta^{t-1})+ L^\prime(\theta^{t-1})\Delta\theta \] 我们想求的\(\theta^t=\theta^{t-1}+\Delta \theta\)
Newton's Method
将\(L(\theta^t)\)在\(\theta^{t-1}\)处进行二阶泰勒展开 \[ \begin{align} L(\theta^t) &= L(\theta^{t-1}+\Delta \theta)\\ &\approx L(\theta^{t-1})+L^\prime(\theta^{t-1})\Delta \theta + L^{\prime\prime}(\theta^{t-1})\frac{\Delta \theta^2}{2} \end{align} \] 记一阶导数和二阶导数分别为\(g\)和\(H\),那么 \[ L(\theta^t)=L(\theta^{t-1})+g\Delta \theta + H\frac{\Delta \theta^2}{2} \] 要使得迭代后的结果尽量小,即\(g\Delta \theta + H\frac{\Delta \theta^2}{2}\)尽量小,那么有\(\frac{\left(g\Delta \theta + H\frac{\Delta \theta^2}{2}\right)}{\partial\Delta\theta}=0\)
求得\(\Delta \theta=H^{-1}g\),故\(\theta^{t}=\theta^{t-1}+\Delta \theta=\theta^{t-1}-\frac{g}{h}\)。如果\(\theta\)是一个向量,那么\(\theta^{t}=\theta^{t-1}-H^{-1}g\),这里\(H\)为海森矩阵。
Gradient Boosting Decision Tree (GBDT)
我们首先来看基于树的Boosting模型中,非常经典的梯度提升树 (Gradient Boosting Decision Tree)。
The Additive Model
首先GBDT是一个加法模型,即最终模型由一系列树模型乘以对应权重相加得来: \[ F_T(x;w)=\sum_{t=0}^T\alpha_t h_t(x;w_t)=\sum_{t=0}^T f_t(x;w_t) \] 我们的目标是使得\(F\)的损失函数最小化: \[ F_T^*=\mathop{\arg\min}\limits_{F}\sum_{i=1}^N L(y_i, F_T(x_i;w)) \]
直接优化这个损失函数复杂度是很高的,GBDT实际上运用了一种类似贪心的策略来优化这个函数,将优化过程分解成了迭代的步骤。
回想梯度下降算法进行优化的步骤,我们有参数\(\theta\),损失函数\(L(\theta)\)是\(\theta\)的函数,我们希望找到最优的\(\theta^*\)使得\(L(\theta^*)\)最小,于是我们使用了迭代优化的步骤。假设迭代执行到第\(t\)步,也就是说我们现在的参数\(\theta^{t-1}\)为前面\(t-1\)步增量之和:\(\theta^{t-1}=\sum_{j=1}^{t-1}\Delta \theta_j\),每一步的增量记为\(\Delta \theta_t\)。当前的增量\(\Delta \theta_{t}\)是怎么计算得到的呢?大家都知道是采用的损失函数在\(\theta^{t-1}\)的负梯度乘以一个步长,即\(\Delta \theta_t=-\alpha_t \frac{\partial L(\theta)}{\partial \theta^{t-1}}\)。
梯度下降相当于是在参数空间\(\theta\)找到最合适的参数\(\theta^*\)使得损失函数\(L(\theta)\)最小化,如果我们把模型\(F_T\)看作是函数空间,我们的目的是在函数空间中找到最优的\(F_T^*\)使得损失函数最小化,在这一个角度上GBDT和梯度下降就统一起来了。每一步的基模型\(f_t\)就相当于梯度下降中的增量\(\Delta \theta\),所以我们就得到了GBDT每一的优化目标,即损失函数\(L\)对于\(F_{t-1}\)的负梯度。
| 梯度下降 | GBDT | |
|---|---|---|
| 损失函数 | \(L(\theta)\) | \(L(F_t)\) |
| 参数 | \(\theta^t\) | \(F_t\) |
| 增量 | \(\Delta \theta_t=-\alpha_t g_t\) | \(f_t=-\alpha_t g_t\) |
| 步长 | \(\alpha_t\) | \(\alpha_t\) |
| 初始值 | \(\theta_0\) | \(f_0\) |
Gradient Boosting Tree for Regression
我们先来讨论GBDT解决回归问题的算法。前面我们已经讨论过,在每一步GBDT的优化目标是损失函数的负梯度,那么现在的问题就是如何求得每一步最优的基模型(GBDT的基模型选用的是CART)。GBDT的算法步骤如下:
Gradient Boosting Tree Algorithm
INPUT: 训练样本\(\{(x_1,y_1),\cdots,(x_m,y_m)\}\),迭代轮数\(T\),损失函数\(L\)
OUTPUT: 强模型\(F_T\)
- 初始化弱学习器\(f_0\),直接使用一个基模型在训练集上进行训练
- 在步骤\(t=1...T\),对于每个样本计算负梯度\(r_{ti}=\left[\frac{\partial L(y_i,F_{t-1}(x_i))}{\partial F_{t-1}}\right]\)
- 在\((x_i,r_{ti})\)上训练得到一个CART回归树,确定树的结构
- 假设一共有\(J\)个叶子节点,那么对每个叶子节点计算最佳输出值\(c_{tj}=\mathop{\arg\min}\limits_{c_{tj}}\sum_{x_i\in R_{tj}} L(y_i,F_{t-1}(x_i)+c_{tj})\)(其中\(c_{tj}\)代表第\(j\)个叶子的输出,\(R_{tj}\)代表第\(j\)个叶子对应的样本集合),确定每个叶子节点的输出
- 更新强学习器\(F_t=F_{t-1}+f_t\),回到步骤2直到达到迭代轮数
- 最终得到强学习器的表达式:\(f(x)=f_0(x)+\sum\limits_{t=1}^T\sum\limits_{j=1}^J c_{tj}\mathrm I(x\in R_{tj})\)
于是我们就得到了最终模型\(F_T\)。
Gradient Boosting Tree for Classification
在处理分类任务时,由于输出是离散的值
一种方法是使用指数损失函数,此时GBDT退化为AdaBoost;另一种方法是借鉴逻辑回归的方法,去建模真实值的概率
Binary Classification
Multi-class Classfication
GBDT Sumarry
优点:
- 可以灵活处理
- 相对SVM,调参较少
- 使用某些损失函数对异常值的鲁棒性高
缺点:
- 难以并行训练
XGBoost
前面我们讲了梯度下降和牛顿法,刚才又讨论了GBDT和梯度下降的关系,那么XGBoost是否和牛顿法有什么关系呢?答案是肯定的。GBDT利用了损失函数在\(F_{t-1}\)的一阶展开(即一阶导数信息),而XGBoost则利用了损失函数在\(F_{t-1}\)的二阶展开,这也是XGBoost和GBDT最根本的区别。下面我们将详细讲解XGBoost算法。
| 牛顿法 | XGBoost | |
|---|---|---|
| 损失函数 | \(L(\theta)\) | \(L(F_t)\) |
| 参数 | \(\theta^t\) | \(F_t\) |
| 增量 | \(\Delta \theta_t=-\alpha_t H^{-1}_tg_t\) | \(f_t=-\alpha_t H^{-1}_tg_t\) |
| 步长 | \(\alpha_t\) | \(\alpha_t\) |
| 初始值 | \(\theta_0\) | \(f_0\) |
Regularization
XGBoost相比GBDT的另一大改进是加入了正则化项,即控制每个树的复杂度。衡量树的复杂度的度量有很多,XGBoost采用的是每棵树叶子节点的个数\(T\)和每个叶子节点输出\(w\)的平方和: \[ \Omega(f)=\gamma T+\frac{1}{2}\lambda\parallel w\parallel^2 \]
这一步主要是为了进一步降低每个弱学习器的方差。
Objective Function
加上正则项之后总的损失函数变为: \[ L=\sum_{i=1}^N \ell(y_i, F_T(x_i))+\Omega(F_T) \] 和GBDT类似,我们来推导第\(t\)步的优化公式,对于第\(t\)步,我们的损失函数为: \[ \begin{align} L_t&=\sum_{i=1}^N \ell(y_i,F_t(x_i))+\Omega(F_t)\\ &=\sum_{i=1}^N \ell(y_i, F_{t-1}(x_i) + f_t(x_i))+\Omega(F_t) \end{align} \] 将损失函数在\(F_{t-1}\)处进行二阶泰勒展开,得到 \[ L_t \approx \left[\sum_{i=1}^N \ell(y_i, F_{t-1}) + g_i f_t(x_i) + \frac{1}{2}h_i f_t^2(x_i) \right] + \Omega(F_t) \] 其中\(g_i=\frac{\partial \ell(y_i, F_{t-1})}{\partial F_{t-1}}\),\(h_i=\frac{\partial \ell(y_i, F_{t-1}) ^2}{\partial^2 F_{t-1}}\),分别代表损失函数对\(F_{t-1}\)的一阶导和二阶导。
由于我们要优化的是本轮的基模型\(f_t\),\(\ell(y_i, F_{t-1})\)已经是固定的了,相当于常数,把常数项去掉,得到: \[ \begin{align} \tilde L_t &= \left[\sum_{i=1}^N g_i f_t(x_i) + \frac{1}{2}h_i f_t^2(x_i) \right] + \Omega(f_t)\\ &=\left[\sum_{i=1}^N g_i f_t(x_i) + \frac{1}{2}h_i f_t^2(x_i) \right] + \gamma T + \frac{1}{2}\lambda \parallel w \parallel^2 \end{align} \] 我们都知道样本\(x_i\)在树\(f_t\)上的输出取决于\(x_i\)在哪个叶子节点。假设树\(f_t\)一共有\(J\)个叶节点,记\(q(x_i)=j\)代表样本\(x_i\)经过决策树对应的叶节点是\(j\),\(I_j\)代表叶子节点\(j\)的所有样本下标集合,\(w_j\)代表叶子节点\(j\)的输出,我们可以将损失函数改写为: \[ \begin{align} \tilde L_t &= \sum_{j=1}^J\left[\sum_{i\in I_j}g_i w_j+\frac{1}{2}(\sum_{i\in I_j}h_i +\lambda)w_j^2\right]+\gamma T\\ &= \sum_{j=1}^J\left[G_j w_j + \frac{1}{2}(H_j+\lambda)w_j^2 \right] + \gamma T \end{align} \] 其中\(G_j=\sum_{i\in I_j}g_i\)和\(H_j=\sum_{i\in I_j}h_i\)为简记,分别代表损失函数在叶子节点\(j\)对应的所有样本上的一阶导之和与二阶导之和。
到现在,我们还剩两个问题需要解决,一个是确定树\(f_t\)的最优结构,也就是怎么去分裂节点,另一个是确定每个叶子节点的最优输出。我们可以先确定下一个问题,找到另一个问题的最优答案,再来确定剩下的问题。
这里先去寻找树\(f_t\)每一个叶子节点对应的最优输出。和牛顿法的推导类似,为了使损失函数下降的最快,我们令\(G_j w_j + \frac{1}{2}(H_j+\lambda)w_j^2\)的导数为\(0\),得到: \[ w_j^*=-\frac{G_j}{H_j + \lambda} \] 加上正则项有: \[ \tilde L_t^*=-\frac{1}{2}\sum_{j=1}^J\frac{G_j^2}{H_j+\lambda}+\gamma T \]
Splitting Strategy
现在来确定树\(f_t\)的最优结构。最优结构的确定实际上使用了一种类似贪心的策略,和决策树类似,我们从一个只有根节点的树出发(所有样本都在根节点这一叶子节点上),不断分裂节点来降低\(\tilde L_t^*\)。在每一步的分裂中,我们会希望\(\frac{G_j^2}{H_j+\lambda}\)越大越好,于是: \[ Gain = \frac{G_L^2}{H_L+\lambda} + \frac{G_R^2}{H_R+\lambda} - \frac{(G_L+G_R)^2}{H_L+H_R+\lambda} - \gamma \]
我们希望挑选能使得\(Gain\)最大的特征和特征分裂点,而选择的策略又有很多种,下面介绍三种。
Exact Greedy Algorithm for Split Finding
最简单的方法是枚举所有特征,然后对于这个特征下的所有可能取值进行排序,然后遍历分裂点,找到使得\(gain\)最高的那个。这样做的好处是找到的分裂点确定是最好的,不过坏处是时间复杂度过高。
Approximate Algorithm for Split Finding
一个比较容易想到的优化方案是不去遍历所有可能的分裂点,而是只考察其中的分位数,如下图展示了三分位数方法:
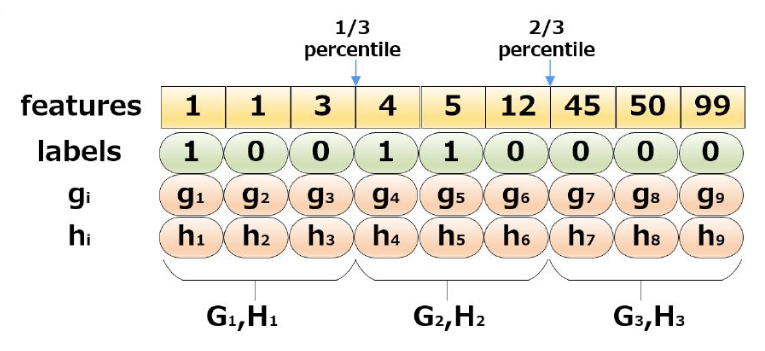
这样需要考察的点就大大减少。
同时分位数的选择由有global和local之分,global是指在训练之前我们就可以提前对每个特征的分位数进行预处理,local是指每次分裂前计算分位数点。直观上来说global需要更多的分位点数,而local则需要更多的计算量。
实际上,XGBoost还会使用二阶导信息\(h_i\)对样本进行夹权,如下图所示:
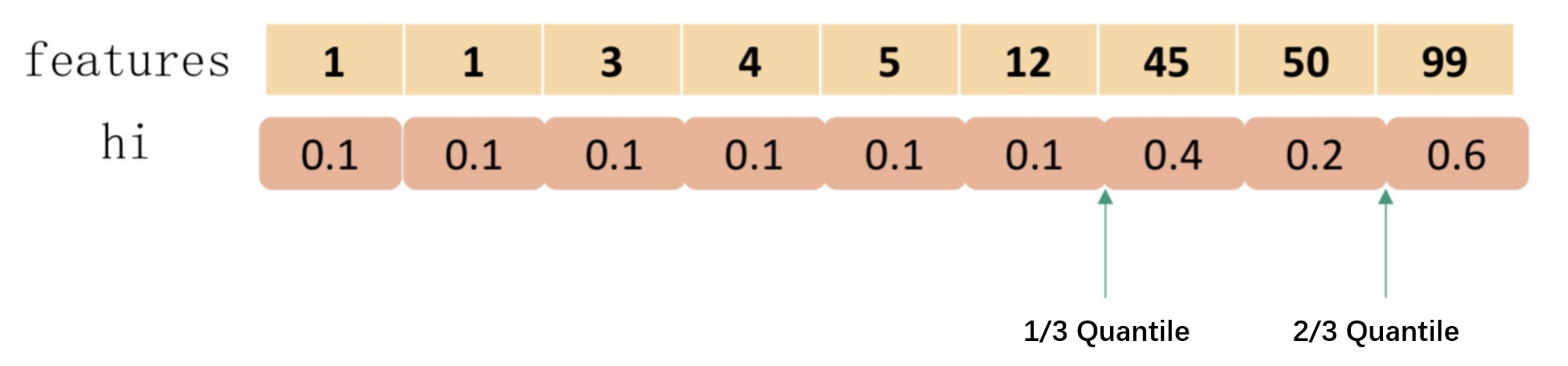
Sparsity-aware Split Finding
稀疏感知分裂算法 (Sparsity-aware Split Finding)
Other Features
除了上面提到的之外,XGBoost还有很多工程优化。
Block Structure and Parallelism
XGBoost预先对特征进行了排序,
每个特征的增益的计算可以并行进行
Column Sample
借鉴随机森林,即每次只用一部分特征进行特征选择,进一步降低过拟合
Shrinkage
在每次迭代会对叶子节点的权总乘以一个系数,让后面的树有更大的学习空间。
Custom Loss Function
Missing Values
LightGBM
本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!