Machine Learning Classification Algorithms: Support Vector Machine

Introduction

Still working on it😅...

blog

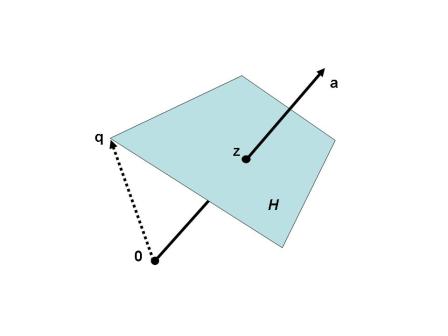
Hyperplane

超平面可以从代数和几何两方面来理解。超平面的代数定义可以看作是方程： \[ a_1x_1+\cdots+a_nx_n=d \] 的所有解形成的集合，其中\(a_1,\cdots,a_n\)为不全为\(0\)的实数，\(d\)也是实数。

从几何上来说，超平面可以看作是除空间\(R^n\)自身外维度最大的仿射空间。

Maximum Margin Classifier

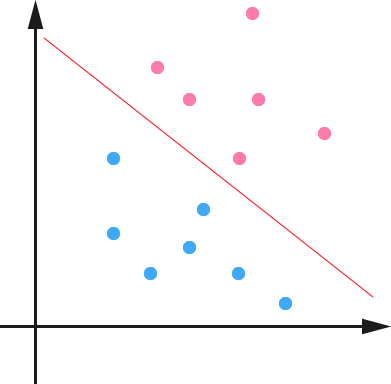
要谈SVM就得先谈线性分类器，其设置是这样的。对于\(D\)维空间，我们有一堆数据\(X\)，进行二分类任务，标签记为\(y\)，其中\(y=-1\)和\(y=1\)分别代表不同的类别。我们的任务就是找到一个超平面，将正负例切分开来（先假设数据是线性可分的），这个超平面的方程可以表示为： \[ w^\top x+b=0 \] 我们令\(f(x)=w^\top x+b\)，对于\(f(x)<0\)的样本，我们赋予其类别\(-1\)，对于\(f(x)>0\)的样本，我们可以赋予其类别\(1\)。对于相同的分类结果，我们可以找出无限种超平面。不过，对于那些样本特别靠近超平面的情况，鲁棒性并不好。为什么呢？因为这时只要超平面有轻微的变化，样本的分类结果就会发生变化。直观上来说，我们希望样本到超平面的距离越大越好。

我们先定义函数间隔的概念，函数间隔\(\hat \gamma=y(w^\top x+b)\)，乘以\(y\)的目的主要是保持非负性，表示起来方便。可见函数间隔的大小并不能表示样本距离，因为同一个超平面，法向量\(w\)可以任意增大，函数间隔也会相应增大。

下面来推导点\(x\)到超平面的距离。设\(x\)在超平面上的投影为\(x_0\)，到超平面的距离为\(\gamma\)，\(w\)为法向量，那么有： \[ x=x_0+\gamma\frac{w}{\parallel w\parallel} \] 将上式带入到超平面方程可以得到 \[ \gamma=\frac{w^\top}{\parallel w\parallel}x+\frac{b}{\parallel w\parallel} \] 我们称\(\gamma\)为几何间隔。

可以很容易看出函数间隔和几何间隔的关系： \[ \gamma = \frac{\hat \gamma}{\parallel w\parallel} \] 前面提到我们希望几何间隔越大越好，于是可以直接最大化\(\gamma\)，得到： \[ \begin{align} \max \space &\gamma\\ s.t. \space & y_i(w^\top x_i+b)=\hat\gamma_i\geq\hat\gamma, \space i=1,\cdots,n \end{align} \] 这里\(\hat \gamma=\gamma \parallel w\parallel\)，根据前面的分析我们知道，对于同一个超平面，函数间隔\(\hat\gamma\)可以随着\(\parallel w\parallel\)的变化而变化，所以为了找到最优的\(\gamma\)，我们可以考虑固定\(\parallel w\parallel\)或者\(\hat\gamma\)，这里我们固定\(\hat \gamma=1\)，所以有： \[ \begin{align} \max & \space \frac{1}{\parallel w\parallel},\\ s.t. \space& y_i(w^\top x_i+b)\geq 1, \space i=1,\cdots,n \end{align} \]

下面的约束条件代表前提是所有样本分类正确，而\(\max\frac{1}{\parallel w\parallel}\)代表最大化间隔。为了方便，我们将其化为等价的最小化形式： \[ \begin{align} \min & \space \frac{1}{2}\parallel w\parallel^2,\\ s.t. & y_i(w^\top x_i+b)\geq 1, \space i=1,\cdots,n \end{align} \] 其中那些\(y_i(w^\top x_i+b)=1\)的样本就是“支持向量”。这个优化问题是典型的二次凸优化问题，可以调用现成的算法去解决。不过我们可以使用拉格朗日乘子法来更高效的解决。

Dual Problem

拉格朗日乘子法可以将有\(d\)个变量和\(k\)个约束条件的最优化问题转化成有\(d+k\)个变量的无约束最优化问题求解。

Lagrange Multiplier

对于以下有约束优化问题： \[ \begin{align} \min_x \space & f(x)\\ \text{s.t.} \space & h_i(x)=0 \space (i=1,\cdots,m),\\ &g_j(x) \leq 0 \space (j=1,\cdots,n) \end{align} \]

引入拉格朗日乘子\(\boldsymbol\lambda = (\lambda_1,\lambda_2,\cdots,\lambda_n)^\top\)和\(\boldsymbol\mu=(\mu_1,\mu_2,\cdots,\mu_m)^\top\)，相应的广义拉格朗日函数 (generalized Lagrange function) 为： \[ L(\boldsymbol x,\boldsymbol\lambda,\boldsymbol\mu)=f(\boldsymbol x)+\sum_{j=1}^n \lambda_j g_j(\boldsymbol x)+\sum_{i=1}^m \mu_i h_i(\boldsymbol x) \]

其中\(\lambda_j\)，\(\mu_i\)被称作是拉格朗日乘子，\(\lambda_j \geq 0\)。

Primal Problem

现在我们来讨论原问题的等价性。假设给定某个\(x\)，如果\(x\)违反约束条件，即存在某个\(x\)使得\(h_i(x)\neq 0\)或者\(g_j(x)>0\)，那么就有： \[ \max\limits_{\boldsymbol\lambda,\boldsymbol\mu:\lambda_j\geq 0} L(\boldsymbol x,\boldsymbol\lambda,\boldsymbol\mu)=+\infty \] 如果存在某个\(x\)使得\(h_i(x)\neq 0\)，那么可以令\(\lambda_j \rightarrow +\infty\)，如果存在\(g_j(x)>0\)，那么可令\(\mu_ih_i(x)\rightarrow +\infty\)。

如果考虑以下极小化问题： \[ p^*=\min_x\max\limits_{\boldsymbol\lambda,\boldsymbol\mu:\lambda_j\geq 0} L(\boldsymbol x,\boldsymbol\lambda,\boldsymbol\mu) \] 他与原始带约束最优化问题是等价的（因为不符合约束时会有\(+\infty\)，而我们考虑的是极小化问题），我们将其记为原问题 (Primal problem)。

Dual Problem

如果先考虑最小化\(x\)，再考虑最大化\(\boldsymbol\lambda\)和\(\boldsymbol\mu\)，这时有： \[ \max\limits_{\boldsymbol\lambda,\boldsymbol\mu:\lambda_j\geq 0}\min_x L(\boldsymbol x,\boldsymbol\lambda,\boldsymbol\mu) \] 对偶问题 (Dual problem) \[ d^*=\max\limits_{\boldsymbol\lambda,\boldsymbol\mu:\lambda_j\geq 0}\min_x L(\boldsymbol x,\boldsymbol\lambda,\boldsymbol\mu) \] 原问题和对偶问题的关系 \[ d^*=\max\limits_{\boldsymbol\lambda,\boldsymbol\mu:\lambda_j\geq 0}\min_x L(\boldsymbol x,\boldsymbol\lambda,\boldsymbol\mu) \leq \min_x\max\limits_{\boldsymbol\lambda,\boldsymbol\mu:\lambda_j\geq 0} L(\boldsymbol x,\boldsymbol\lambda,\boldsymbol\mu) = p^* \]

KKT Condition

对于原问题和对偶问题，设\(f(x)\)和\(g_i(x)\)为凸函数，\(h_i(x)\)为仿射函数，并且不等式约束\(c_i(x)\)是严格可行的，则\(x^*\)，\(\lambda^*\)，\(\mu^*\)分别是原问题和对偶问题的解的充分必要条件是满足下面的Karush-Kuhn-Tucker (KKT) 条件： \[ \begin{cases} \nabla_x L(x^*,\lambda^*,\mu^*)=0 &\\ \lambda^*_j g_j(x^*)=0 & j=1,\cdots n\\ g_j(x^*)\leq 0 & j=1,\cdots n\\ \lambda_j^*\geq 0 & j=1,\cdots n\\ h_i(x^*) = 0 & i = 1, \cdots m \end{cases} \]

这告诉我们

Dual Form of SVM Optimization

支持向量机优化的对偶问题可以写为： \[ L(w,b,\alpha)=\frac{1}{2}\parallel w\parallel^2-\sum_{i=1}^n \alpha_i(y_i(w^\top x_i+b)-1) \] 我们先令： \[ \begin{align} \frac{\partial L}{\partial w}=0&\Rightarrow w=\sum_{i=1}^n\alpha_i y_i x_i\\ \frac{\partial L}{\partial b}=0&\Rightarrow \sum_{i=1}^n\alpha_i y_i =0 \end{align} \] 带回到\(L\)得到： \[ \begin{align} L(w,b,\alpha)&=\frac{1}{2}\sum_{i,j=1}^n\alpha_i\alpha_j y_i y_j x^\top_i x_j-\sum_{i,j=1}^n \alpha_i\alpha_jy_iy_jx^\top_ix_j-b\sum_{i=1}^n\alpha_iy_i+\sum_{i=1}^n\alpha_i\\ &=\sum_{i=1}^n \alpha_i - \frac{1}{2}\sum_{i,j=1}^n \alpha_i\alpha_j y_i y_j x^\top_i x_j \end{align} \] 于是得到关于\(\alpha\)的对偶优化问题： \[ \begin{align} \max_\alpha &\sum_{i=1}^n \alpha_i - \frac{1}{2}\sum_{i,j=1}^n \alpha_i\alpha_j y_i y_j x^\top_i x_j\\ \text{s.t. }& \alpha_i\geq 0, i=1,\cdots,n\\ & \sum_{i=1}^n \alpha_i y_i = 0 \end{align} \]

前面有提到我们根据\(f(x)=w^\top x + b\)的输出来判定样本类别，而刚才得到\(w=\sum_{i=1}^n\alpha_i y_i x_i\)，于是： \[ \begin{align} f(x) &= (\sum_{i=1}^n \alpha_iy_ix_i)^\top x+b\\ &= \sum_{i=1}^n \alpha_i y_i \langle x_i, x\rangle + b \end{align} \] 最后的\(\sum_{i=1}^n \alpha_i y_i \langle x_i, x\rangle + b\)值得特别注意，这意味着我们对于测试样本\(x\)的预测，只需要计算它与训练集的内积即可，同时由于所有非支持向量对应的\(\alpha\)都是\(0\)，我们只需要求一小部分内积。同时这个内积计算也是后面核方法应用的前提。

Kernel

到目前为止，我们的讨论都是在数据是线性可分的前提下进行讨论的，那么对于线性不可分的情况呢？答案是使用核方法。

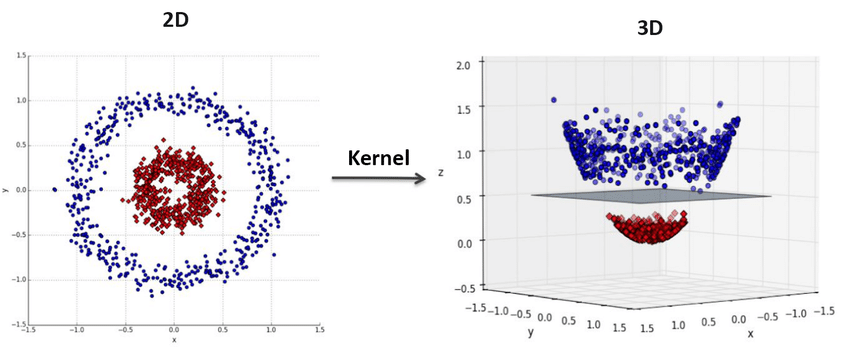
核方法的思想是，对于原始不可分的数据，我们假设原始数据通过一个映射\(\phi(\cdot)\)就变得线性可分了。核方法相当于对数据找到了一种新的表示，如上图没法用一个超平面直接分割，但通过\(\phi(\cdot)\)映射之后就变得可分了。原始的分类函数为： \[ f(x)= \sum_{i=1}^n \alpha_i y_i \langle x_i, x\rangle + b \] 加上映射之后变为： \[ f(x)= \sum_{i=1}^n \alpha_i y_i \langle \phi(x_i), \phi(x)\rangle + b \] 优化问题也变为： \[ \begin{align} \max_\alpha &\sum_{i=1}^n \alpha_i - \frac{1}{2}\sum_{i,j=1}^n \alpha_i\alpha_j y_i y_j \langle\phi(x_i), \phi(x_j)\rangle\\ \text{s.t. }& \alpha_i\geq 0, i=1,\cdots,n\\ & \sum_{i=1}^n \alpha_i y_i = 0 \end{align} \] 我们把计算两个向量在映射后的空间中的内积的函数叫做核函数 \[ f(x)= \sum_{i=1}^n \alpha_i y_i k(x_i, x) + b \] 优化问题改为： \[ \begin{align} \max_\alpha &\sum_{i=1}^n \alpha_i - \frac{1}{2}\sum_{i,j=1}^n \alpha_i\alpha_j y_i y_j k(\phi(x_i), \phi(x_j))\\ \text{s.t. }& \alpha_i\geq 0, i=1,\cdots,n\\ & \sum_{i=1}^n \alpha_i y_i = 0 \end{align} \] 实际上，通过核函数，我们隐式地定义了一个映射\(\phi(\cdot)\)

常用核函数

名称	表达式	参数
线性核
多项式核
RBF核
拉普拉斯核
Sigmoid核

Soft Margin

数据线性不可分的情况，除了数据本身结构非线性的原因之外（核方法），还有可能是因为噪声或者离群点。为了处理这种情况，我们可以允许一部分点在一定程度上偏离超平面，具体来说就是原来的约束条件\(y_i(w^\top x_i+b)\geq 1, \space i=1,\cdots,n\)变成了： \[ y_i(w^\top x_i+b)\geq 1-\xi_i, \space i=1,\cdots,n \] 其中\(\xi_i\geq 0\)称作是松弛变量，代表样本\(i\)允许的偏离程度。当然松弛变量不可能无限大，所以我们需要将\(\xi_i\)加入到优化目标函数中使其尽量小，于是有： \[ \begin{align} \min & \space \frac{1}{2}\parallel w\parallel^2+C\sum_{i=1}^n \xi_i,\\ s.t. & y_i(w^\top x_i+b)\geq 1-\xi_i, \space i=1,\cdots,n \end{align} \] 其中\(C\)为控制最优化\(\parallel w\parallel\)和松弛变量这两项的权重。这里的优化函数还是对偶问题之前的形式，我们马上会讨论对偶问题。

Numerical Optimization

这里讨论SVM高效求解的Sequential Minimal Optimization (SMO)算法。

坐标下降法是一种非梯度优化算法，