Unsupervised Representation Learning by Predicting Random Distances
本文最后更新于:1 年前
Introduction
针对高维表格数据的表示学习,作者提出了基于预测预计变换后的距离的无监督表示学习框架RDP,并进行了理论上的讨论。To be finished...
Proposed Method
Random Distance Prediction Model
对于很多下游任务来说,高维数据对模型效率和性能都很大,所以学习低维的有意义(能够最大限度保存原始空间的信息)的表示十分重要。本文的大致思想是给定一个确定的随机映射将样本映射到一个新的空间,然后构造数据集,输入时任意一对样本,标签是两个样本在新的空间的距离,之后训练一个模型来学习这个距离。作者认为通过该任务的训练,模型能够学到有意义的低维表示。模型的框架如下图:
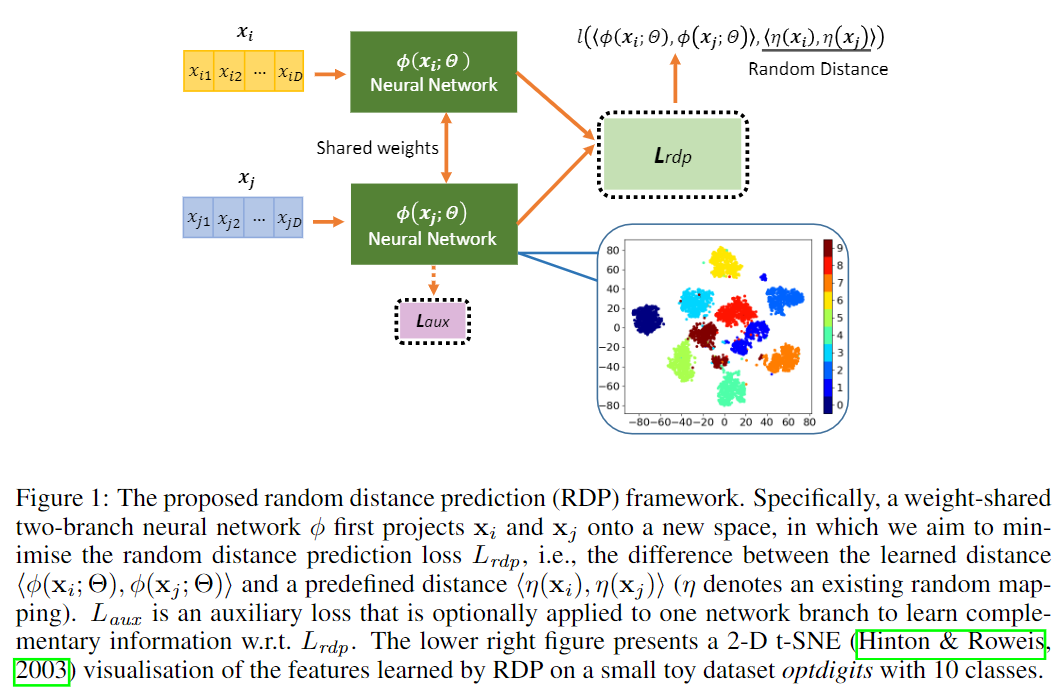
其中\(\phi(\mathbf x;\Theta):\mathbb R^D\mapsto\mathbb R^M\)为孪生神经网络(Siamese Neural Network),将数据映射到\(M\)的新空间。损失函数为:
\[ \mathcal L_{rdp}(\mathbf x_i,\mathbf x_j)=l(\langle \phi(\mathbf x_i;\Theta),\phi(\mathbf x_j;\Theta)\rangle,\langle\eta(\mathbf x_i),\eta(\mathbf x_j)\rangle) \]
其中\(\eta(\cdot)\)为已知的映射,\(l(\cdot)\)为衡量两个输入相似程度的度量。具体的来说,文中选取了简单的实现方案,即采用内积作为映射后的样本的距离度量:
\[ \mathcal L_{rdp}(\mathbf x_i,\mathbf x_j)=\left(\phi(\mathbf x_i;\Theta)\cdot\phi(\mathbf x_j;\Theta)-\eta(\mathbf x_i)\cdot\eta(\mathbf x_j)\right)^2 \]
\(\eta(\cdot)\)为现成的映射。至于为什么要这么做,可以先接着看下面原文给出的理论分析,然后我再说说我自己的理解。
Incorporating Task-Dependent Complementary Auxiliary Loss
对于特定的下游任务,作者提出可以整合额外的误差函数来提高模型行性能。比如说针对聚类任务可以使用重构误差:
\[ \mathcal L_{aux}^{clu}(\mathbf x)=(\mathbf x-\phi^\prime(\phi(\mathbf x;\Theta); \Theta^\prime))^2 \]
其中\(\phi(\cdot)\)和\(\phi^\prime(\cdot):\mathbb R^M\mapsto\mathbb R^D\)分别为编码器和解码器。
对于异常检测任务,可以使用下式: \[ \mathcal L_{aux}^{ad}(\mathbf x)=(\phi(\mathbf x;\Theta)-\eta(\mathbf x))^2 \]
这一个Loss本来是出现在强化学习的论文中,用来检测一个状态\(\mathbf x\)出现的频率,如果预测误差较小,说明这个样本之前见过或见过类似的,否则没怎么见过,可以认为是异常。由于本文的目的主要是降维加保留原始空间信息,可以认为使用线性变换的话此目的已经达到了。
Theoretical Analysis
Using Linear Projection
这里讨论使用线性映射的情况,设数据集\(\mathcal X\subset\mathbb R^{N\times D}\),映射矩阵\(\mathbf A\subset\mathbb R^{K\times D}\)为一随机矩阵,映射之后的数据为\(\mathbf A\mathcal X^\top\)。对于\(\epsilon\in(0,\frac{1}{2})\)和\(K=\frac{20\log n}{\epsilon^2}\),存在\(f:\mathbb R^D\mapsto\mathbb R^K\)使得对于所有的\(\mathbf x_i,\mathbf x_j\in\mathcal X\)有:
\[ (1-\epsilon)\parallel\mathbf x_i-\mathbf x_j \parallel^2\leq \parallel f(\mathbf x_i)-f(\mathbf x_j)\parallel^2\leq (1+\epsilon)\parallel\mathbf x_i-\mathbf x_j\parallel^2 \]
如果\(\mathbf A\)的每个元素独立采样自标准正态分布那么有:
\[ \text{Pr}\left((1-\epsilon)\parallel\mathbf x\parallel^2\leq\parallel\frac{1}{\sqrt{K}}\mathbf A\mathbf x\parallel^2\leq(1+\epsilon)\parallel\mathbf x\parallel^2\right)\geq 1-2e^{\frac{-(\epsilon^2-\epsilon^3)K}{4}} \]
在该随机映射下有:
\[ \text{Pr}(|\hat{\mathbf x}_i\cdot\hat{\mathbf x}_j-f(\hat{\mathbf x}_i)\cdot f(\hat{\mathbf x}_j)|\geq\epsilon)\leq 4e^{\frac{-(\epsilon^2-\epsilon^3)\cdot K}{4}} \]
直观的解释就是说使用线性映射的情况下,只要使用的变换矩阵采样自标准正态分布,那么变换之后样本对之间的距离信息能够以一定的概率保留。
Using Non-Linear Projection
这里作者试图说明,在某些条件下,非线性随机映射的作用和核函数接近。对于一个确定的随机映射函数\(g:\mathbb R^D\mapsto\mathbb R^K\),在某些特定的条件下,函数\(g\)和核函数存在下列关系:
\[ k(\mathbf x_i,\mathbf x_j)=\langle\psi(\mathbf x_i),\psi(\mathbf x_j)\rangle\approx g(\mathbf x_i)\cdot g(\mathbf x_j) \]
这个条件是函数\(g\)为一个乘以一个线性矩阵\(\mathbf A\)然后在经过一个具备平移不变性的傅里叶基函数(如cosine)。由于核函数能够保留原始空间的信息,所以作者认为使用非线性函数也能保留原始空间的信息。
PS: 感觉作者在理论部分的讨论还是有点模糊,因为把一个随机的映射作为(伪)监督信息来进行学习,神经网络学到的不也就是随机噪声信息吗?对于这个方法work的原因,我在这里不负责任的分析一下。
Learning Class Structure by Random Distance Prediction
这一节主要解释为什么神经网络\(\phi(\cdot)\)学到的要比随机映射\(\eta(\cdot)\)要好。模型的优化目标可以写成如下的形式:
\[ \mathop{\arg\min}_{\Theta}\sum_{\mathbf x_i,\mathbf x_j\in\mathcal X}(\phi(\mathbf x_i;\Theta)\cdot\phi(\mathbf x_j;\Theta)-y_{ij})^2 \]
其中\(y_{ij}=\eta(\mathbf x_i)\cdot\eta(\mathbf x_j)\)。设\(\mathbf Y_\eta\in\mathbb R^{N\times N}\)为距离矩阵。这个目标函数是在最小化每一对样本在经过\(\phi(\cdot)\)和\(\eta(\cdot)\)映射后之间的距离的差距。通过公式(7)和公式(8)我们知道,在合适的条件下,随机映射\(\eta(\cdot)\)能够保留原始空间的距离信息(即原始空间相近的样本在映射后也相近)。不过,上述公式的成立都依赖于对数据分布的一定假设,当真实的数据不满足条件时,结论就会有所偏差。
Experiments
Performance Evaluation in Anomaly Detection
Experimental Settings
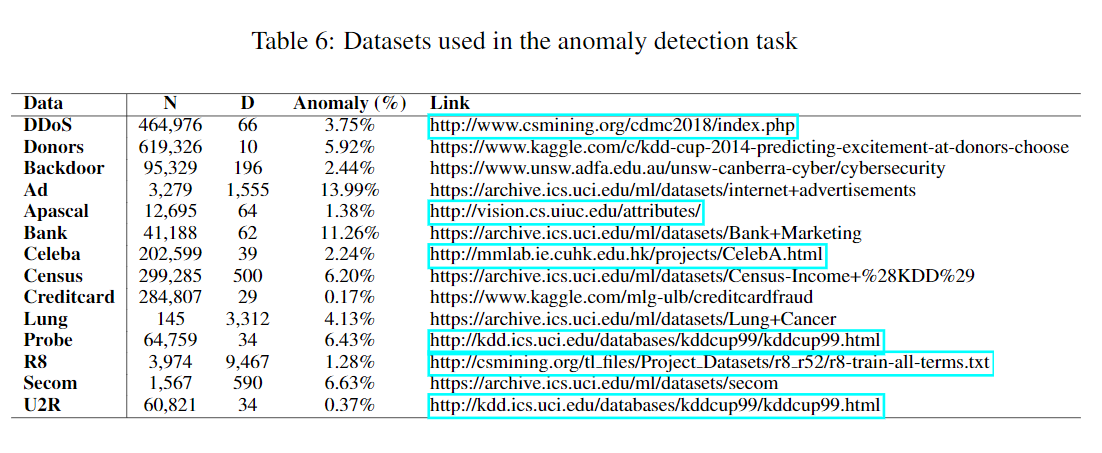
异常分数定义为\(\mathcal S(\mathbf x)=(\phi(\mathbf x;\Theta)-\eta(\mathbf x))^2\)。
Comparison to the State-of-the-art Competing Methods
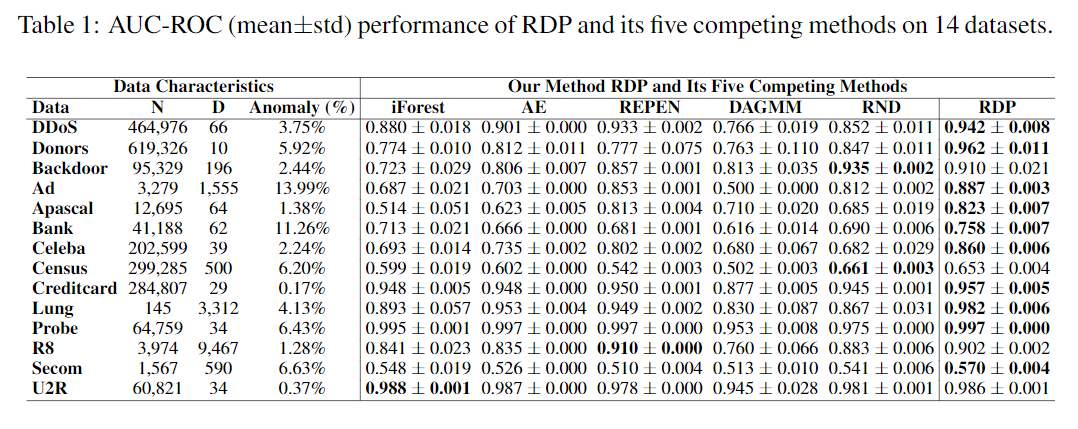
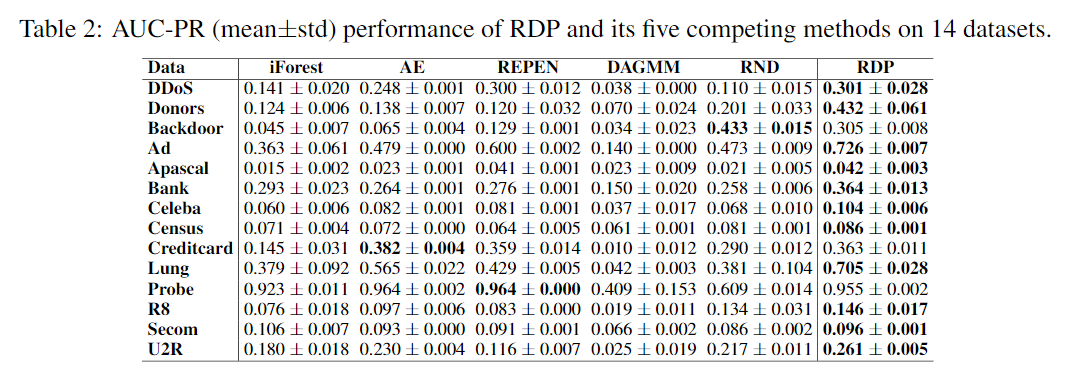
Ablation Study
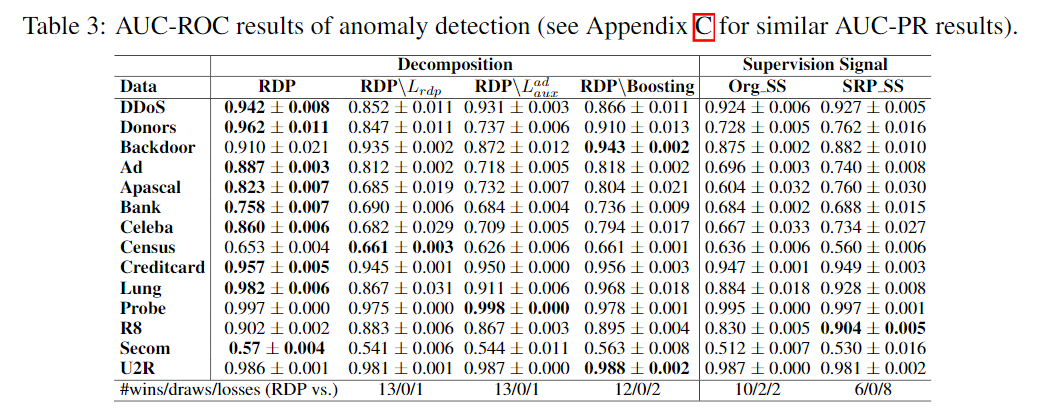
Performance Evaluation in Clustering
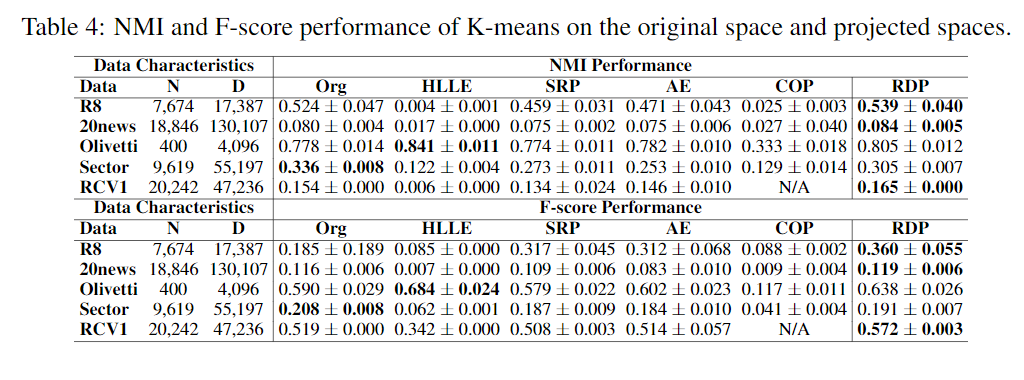
Experimental Settings

Comparison to the State-of-the-art Competing Methods
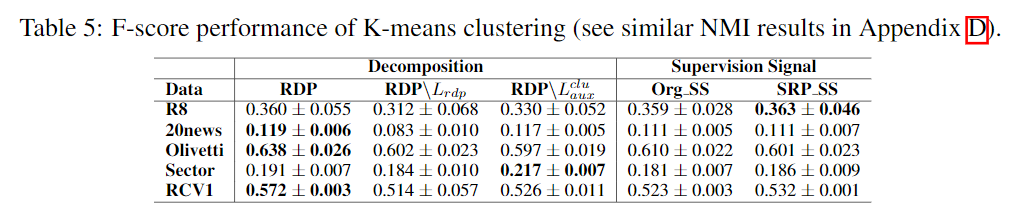
本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!