Effective End-to-end Unsupervised Outlier Detection via Linear Priority of Discriminative Network

Introduction

本文针对无监督异常检测提出了\(E^3\space{Outlier}\)。作者使用自监督学习的方法，通过构建有监督任务在没有标签的情况下学习高层语义特征。PS：这篇文章的方法和NIPS18上的Deep Anomaly Detection Using Geometric Transformations（后面简称GEOM）颇为相似，但是不知为啥没有在实验中进行比较。后面我会分析一些两篇文章方法上的异同。

Proposed Method

Surrogate Supervision Based Effective Representation Learning for UOD

这里作者提到了使用重构的模型来进行异常检测的不足：重构模型采用像素级别的损失函数（如mean square error），而这太过于严格和细节，并不能学到高层语义特征。

为此，作者提出了surrogate supervision based discriminative network (SSD)。具体操作和GEOM类似，首先预定义大小为\(K\)的几何变换集合\(\mathcal O=\{O(\cdot|y)\}_{y=1}^K\)。对每一个样本\(\mathbf x\)，在经过\(K\)个集合变换之后会得到\(K\)个变换后的样本（第\(y\)个变换产生的样本即记为\(\mathbf x^{(y)}=O(\mathbf x|y)\)），每个样本对应的pseudo label即为变换的序号或者说种类。之后在新的数据集上（大小为原来的\(K\)倍）训练\(K\)分类网络。网络的输出为\(P(\mathbf x^{(y^\prime)}|\boldsymbol\theta)=[P^{(y)}(\mathbf x^{(y^\prime)}|\boldsymbol\theta)]_{y=1}^K\)，每个维度代表输入样本对应的变换的概率。总的损失函数为： \[ \min_\theta\frac{1}{N}\sum_{i=1}^{N}\mathcal L_{SS}(\mathbf x_i|\theta) \]

其中\(\mathcal L_{SS}(\mathbf x_i|\theta)\)代表每个样本对应的Loss，这个Loss可以由分类器在\(K\)个变换上的交叉熵损失来确定：

\[ \mathcal L_{SS}(\mathbf x_i|\boldsymbol\theta)=-\frac{1}{K}\sum_{y=1}^K\log(P^{(y)}(\mathbf x_i^{(y)}|\boldsymbol\theta))=-\frac{1}{K}\sum_{y=1}^K\log(P^{(y)}(O(\mathbf x_i|y)|\boldsymbol\theta)) \]

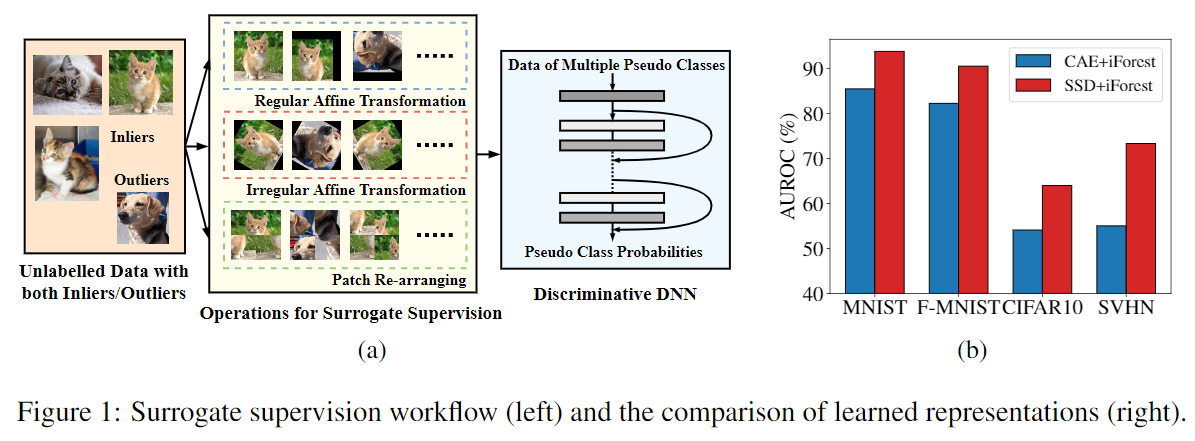
变换集合\(\mathcal O\)由一系列基本变换的组合确定。作者将这些基本变换分为了：1) 旋转 2) 翻转 3) 平移，包括横向和纵向 4) Patch置换（参考图1(a)中的Patch Re-arranging）。最终的变换集合\(\mathcal O\)由三个子集组成，分别是\(\mathcal O_{RA}\)（代表Regular Affine，其中每个变换为旋转\(90°\)的倍数、翻转、横向平移和纵向平移这四个基本变换的叠加），\(\mathcal O_{IA}\)（代表Irregular Affine，其中每个变换为进行\(30°\)的倍数且不为\(90°\)的倍数角度的旋转、翻转这两个基本变换的叠加）和\(\mathcal O_{PR}\)（只包含Patch Re-arranging）。

为了验证SSD学到的特征的有效性，作者将CAE提取的特征和SSD提取的特征分别用孤立森林进行异常检测，发现SSD效果更好（见图1(b)）。

到这里为止本文和GEOM基本没有大的区别。值得注意的是在所采用的几何变换中，采用了非线性变换（进行\(30°\)的倍数且不为\(90°\)的倍数角度的旋转）。而在GEOM中，提到过使用非线性变换的话效果会比较差，至于具体的影响如何，可能需要实验来确定。

Inlier Priority: The Foundation of End-to-end UOD

在这里作者主要对在训练集包含少量异常的情况下做出的理论分析，作者将其称为Inlier Priority，原句如下：

Inlier Priority: Despite that inliers/outliersare indiscriminately fed into SSD for training, SSD will prioritize the minimization of inliers’ loss.

Priority by Gradient Magnitude

对于第\(c\)个类来说，设softmax层和倒数第二层之间的权重矩阵为\(\mathbf w_c=[w_{s,c}]^{(L+1)}_{s=1}\)，损失函数记为\(\mathcal L\)，梯度记为\(\nabla_{\mathbf w_c}\mathcal L=[\nabla_{w_{s,c}}\mathcal L]^{(L+1)}_{s=1}\)。设训练集\(X^{(c)}\)包含\(N_{in}\)个正常样本，\(N_{out}\)个异常样本。记正常样本和异常样本对应的梯度分别为\(\parallel\nabla^{(in)}_{\mathbf w_c}\mathcal L\parallel\)和\(\parallel\nabla^{(out)}_{\mathbf w_c}\mathcal L\parallel\)，在网络只有一个隐层且采用Sigmoid作为激活函数时，两者梯度的期望之比有如下关系：

\[ \frac{E(\parallel\nabla^{(in)}_{\mathbf w_c}\mathcal L\parallel^2)}{E(\parallel\nabla^{(out)}_{\mathbf w_c}\mathcal L\parallel^2)}\approx\frac{N^2_{in}}{N^2_{out}} \]

在训练集中，正常样本和异常样本的数量是极不均衡的，\(N_{in}\gg N_{out}\)，所以有\(E(\parallel\nabla^{(in)}_{\mathbf w_c}\mathcal L\parallel^2)\gg E(\parallel\nabla^{(out)}_{\mathbf w_c}\mathcal L\parallel^2)\)。

在使用更复杂的网络时，作者通过实验展示了正常样本和异常样本对应的梯度大小的比较：

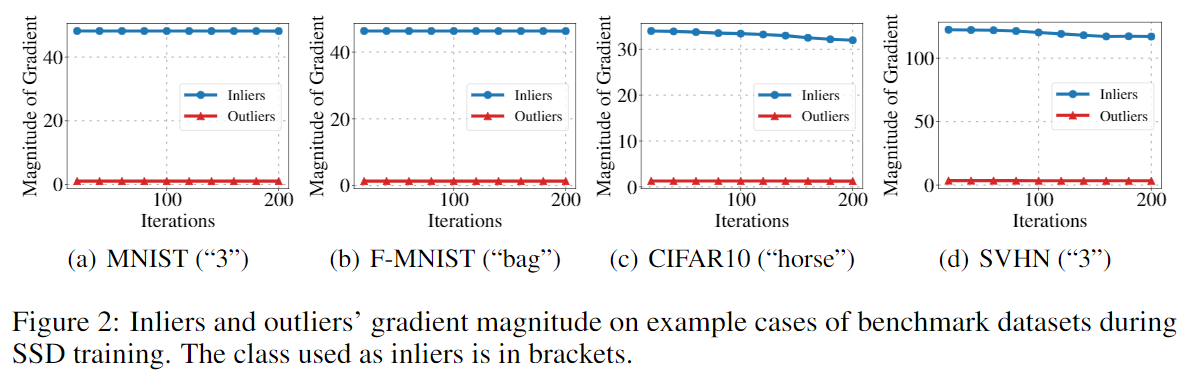
Priority by Network Updating Direction

这里作者通过梯度更新的方向来进行了理论上的解释。对于一个Batch的数据\(X\)，梯度为\(-\nabla_\theta\mathcal L(X)=-\frac{1}{N}\sum_i\nabla_\theta\mathcal L(\mathbf x_i)\)，如果将该梯度在Batch中某一样本\(\mathbf x_i\)对应的梯度的方向上进行分解\(-\nabla_\theta\mathcal L(\mathbf x_i):d_i=-\nabla_\theta\mathcal L(X)\cdot\frac{-\nabla_\theta\mathcal L(\mathbf x_i)}{\parallel -\nabla_\theta\mathcal L(\mathbf x_i)\parallel}\)，这代表了总的Loss在多大程度上减小样本\(\mathbf x_i\)对应的Loss，由于一个Batch即包含正常样本，也可能包含异常样本，所以作者将两者对应的梯度方向贡献进行了可视化：

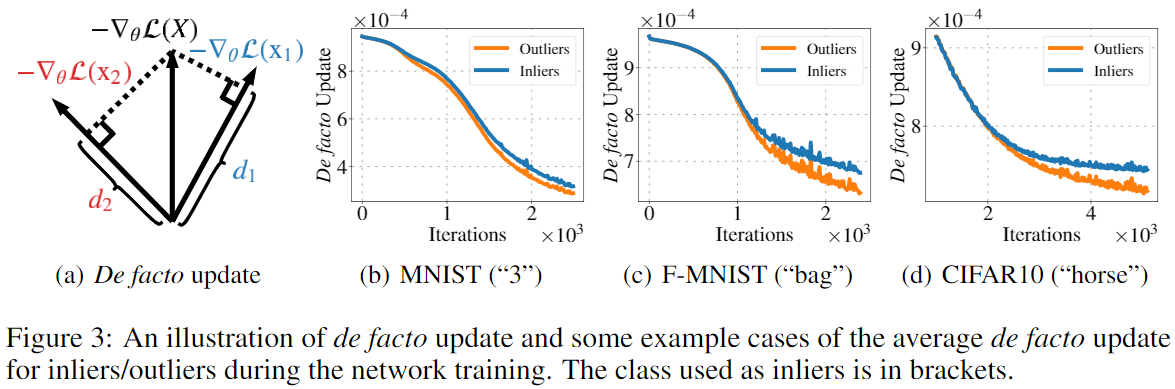
可以看到随着训练的进行，正常样本对应的贡献更高。

PS: 我以为作者会对基于几何变换的异常检测为什么有效做一些理论上的解释，不过却没有。这里只是对在训练集包含少量异常的情况下做出的理论分析，而这个实际上直觉上就很显然了。

Scoring Strategies for UOD

作者采用了三种方法来计算异常分数：

Pseudo Label based Score (PL)

对于一个测试样本\(\mathbf x\)，对其进行\(K\)个几何变换，通过分类器会得到\(K\)个输出，对于第\(k\)个输出，我们只取其第\(k\)个分量，最后把他们加起来除以\(K\)：

\[ S_{pl}(\mathbf x)=\frac{1}{K}\sum_{y=1}^K P^{(y)}(\mathbf x^{(y)}|\boldsymbol\theta) \]

Maximum Probability based Score (MP)

这里稍有不同，对于第\(k\)个输出，我们取其值最大的分量，而不是第\(k\)个分量：

\[ S_{mp}(\mathbf x)=\frac{1}{K}\sum_{y=1}^K\max_t P^{(t)}(\mathbf x^{(y)}|\boldsymbol\theta) \]

Negative Entropy based Score (NE)

作者认为，标签为One-Hot向量，分类器的输出分布越“尖峰”就越接近于正常样本，而越“平均”就越接近于异常样本，所以作者提出使用熵来描述分类器输出的“尖锐度”： \[ S_{ne}(\mathbf x)=-\frac{1}{K}\sum_{y=1}^K H(P(\mathbf x^{(y)}|\boldsymbol\theta))=\frac{1}{K}\sum_{y=1}^K\sum_{t=1}^K P^{(t)}(\mathbf x^{(y)}|\boldsymbol\theta)\log(P^{(t)}(\mathbf x^{(y)}|\boldsymbol\theta)) \] 这里作者对第一种方法得到的结果进行了可视化：

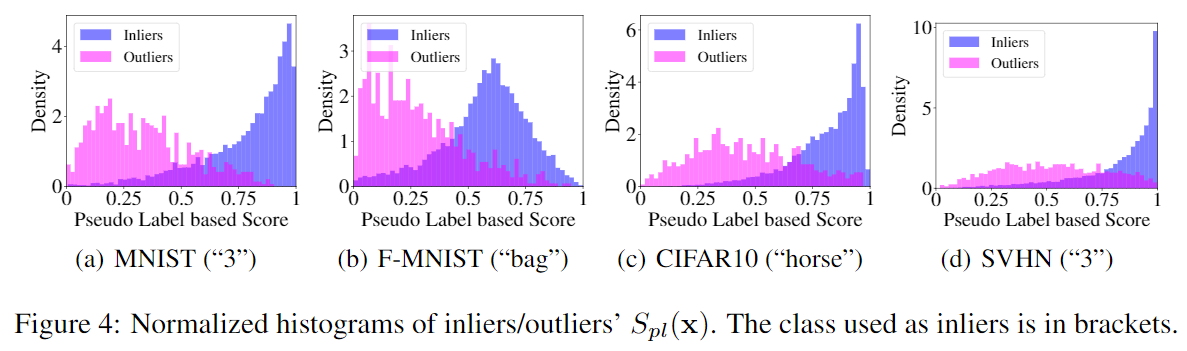
PS：对比NIPS18 的Dirichlet Normality Score

1. 也用到了全部\(K\)个维度的信息
2. 相当于对分类器的输出做了迪利克雷分布的先验假设，然后通过训练集的输出估计分布参数。因为直觉上对于正常分布来说，分类器的输出分布形状上都类似一个尖峰，但对于不同的数据集来说具体形状还是会有所差异

Experiments

Experiment Setup

数据集用到了MNIST, Fashion-MNIST (F-MNIST) , CIFAR10, SVHN和CIFAR100。为了模拟无监督异常检测的环境，人为在训练集中加入异常样本，异常的比例\(\rho\)从\(5\%\)到\(25\%\)以\(5\%\)的步长递增。评测标准采用AUPR和AUROC。

UOD Performance Comparison and Discussion

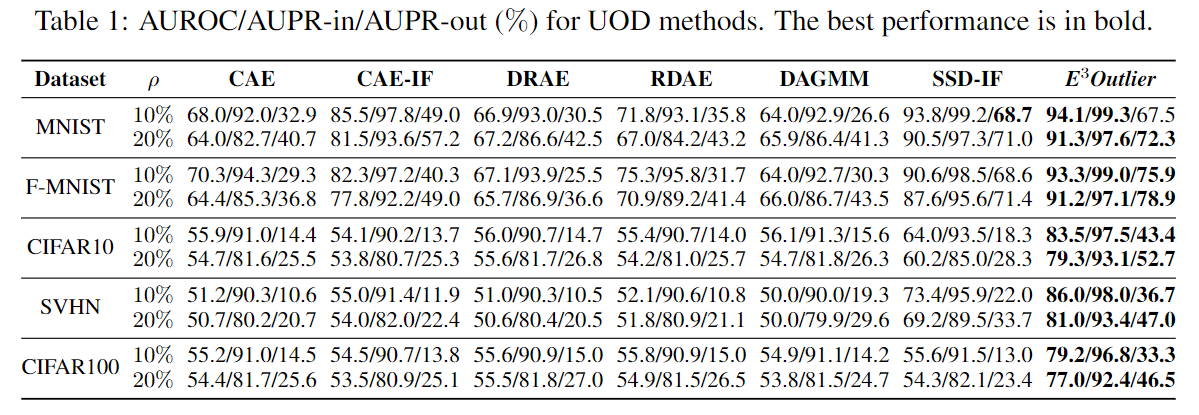
下表展示了模型性能对比结果：

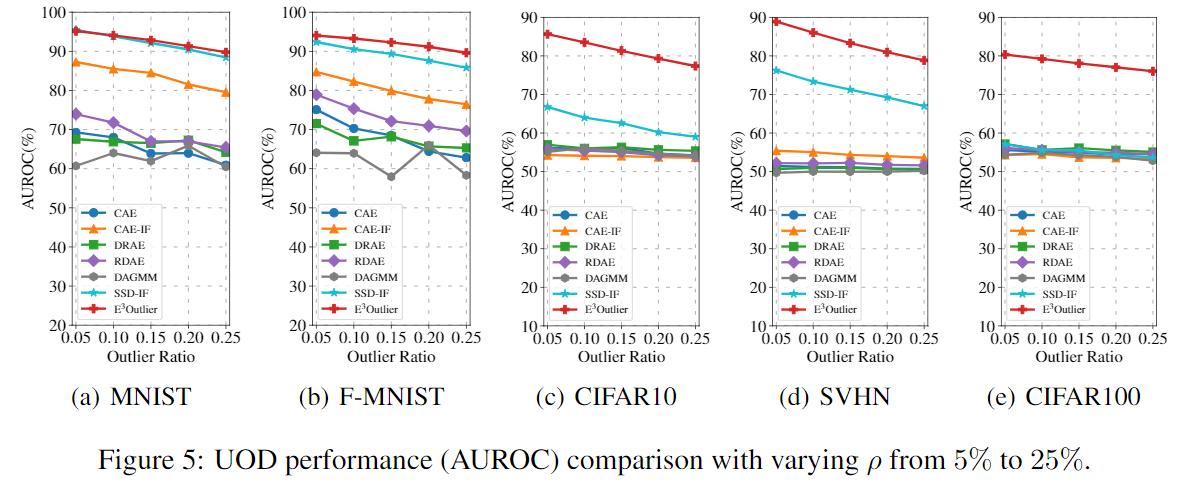
下图展示了在不同的Outlier Ratio下的性能对比：

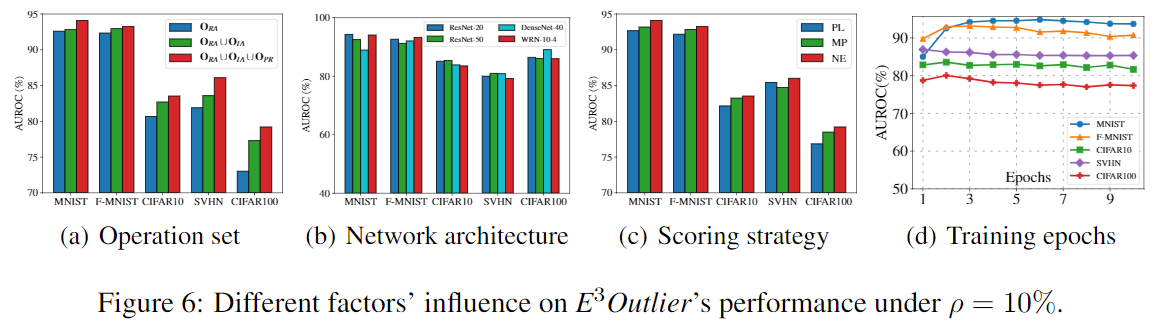
下图展示了在不同的变换集合，网络结构，异常分数的条件下的性能：