Probability Distributions - Binary and Multinomial Variables

Overview

本文主要是介绍一些机器学习中常用的分布，内容主要来自PRML (Pattern Recognition and Machine Learning) 第二章Probability Distributions笔记的第一部分，主要包括2.1. Binary Variables和2.2. Multinomial Variables这两节。

Probability Distributions for Binary Variables

Intro

这一节主要针对二值随机变量的建模，即\(x\in\{0,1\}\)。这里可以想象为我们有一个硬币，\(x=1\)代表正面朝上，而\(x=0\)代表反面朝上，并且正面朝上的概率为\(\mu\)，即： \[ p(x=1|\mu)=\mu \] 其中\(0\leqslant \mu \leqslant 1\)。\(x\)的概率分布可以写为： \[ \text{Bern}(x|\mu)=\mu^x(1-\mu)^{1-x} \] 也就是我们熟知的伯努利分布 (Bernoulli Distribution)。其均值和方差分别为： \[ \begin{align} \mathbb E[x]&=\mu\\ \text{var}[x] &= \mu(1-\mu) \end{align} \] 现在来考虑参数估计任务。假设我们正在进行一个投硬币的实验，每一次投币都服从伯努利分布且相互独立，我们将每次采集到的观测值组成数据集\(\mathcal D=\{x_1,\cdots,x_N\}\)，则似然函数为： \[ p(\mathcal D|\mu)=\prod_{n=1}^N p(x_n|\mu)=\prod_{n=1}^N \mu^{x_n}(1-\mu)^{1-x_n} \] 如果采用极大似然估计的话，我们可以最大化似然函数，这等价于最大化对数似然： \[ \ln p(\mathcal D|\mu)=\sum_{n=1}^{N}\ln p(x_n|\mu)=\sum_{n=1}^N\{x_n\ln\mu+(1-x_n)\ln(1-\mu)\} \] 令其导数为0得到极值点： \[ \mu_{ML}=\frac{1}{N}\sum_{n=1}^N x_n \] 这相当于样本均值，不过这样做会有严重的问题。假设我们的数据集为\(\mathcal D=\{1,1,1\}\)，也就是说我们只收集到了三个样本，并且都是正例，我们会得到\(\mu_{ML}=1\)，而这显然是严重过拟合的。稍后我们会说说如何应对这种情况（加入先验）。

Binomial Distribution

我们同样可以对多次伯努利实验进行概率建模。记\(m\)为成功的次数，\(N\)为数据集大小，可知这个概率应该与\(\mu^m(1-\mu)^{N-m}\)成正比。乘以标准化系数后即我们熟知的二项分布 (Binomial Distribution)： \[ \text{Bin}(m|N,\mu)=\binom{N}{m}\mu^m(1-\mu)^{N-m} \]

其中： \[ \binom{N}{m}=\frac{N!}{(N-m)!m!} \] 其均值和方差分别为： \[ \begin{align} \mathbb E[m]&=N\mu\\ \text{var}[m]&=N\mu(1-\mu) \end{align} \]

Beta Distribution

现在我们来讨论如何解决刚才提到的最大似然估计过拟合问题。为了解决这个问题，我们使用贝叶斯的思路，对\(\mu\)引入了先验分布\(p(\mu)\)。而这个分布需要具有良好的解释性和数学性质。

根据贝叶斯定理： \[ p(\mu|\mathcal D)=\frac{p(\mathcal D|\mu)p(\mu)}{p(\mathcal D)} \] 而\(p(\mathcal D)=\int_0^1 p(\mathcal D|\mu)p(\mu)\mathrm d\mu\)只受数据集影响，而数据集是固定的，所以为常数，因此\(p(\mu|\mathcal D)\propto p(\mathcal D|\mu)p(\mu)\)。而似然函数为\(\mu^x(1-\mu)^{1-x}\)的乘积，如果先验也采用\(\mu\)和\(1-\mu\)的幂的乘积的形式，那么后验分布也将和先验形式相同，这种性质在统计学中被称为先验共轭 (conjugacy)。

这里我们直接给出这个先验分布，再来分析它的性质。这个分布叫做Beta分布 (Beta Distribution)\(P(\mu|a,b)\sim \text{Beta}(a,b)\)： \[ \begin{align} \text{Beta}(\mu|a,b) &= \frac{\Gamma(a+b)}{\Gamma(a\Gamma(b)}\mu^{a-1}(1-\mu)^{b-1}\\ &= \frac{1}{B(a,b)}\mu^{a-1}(1-\mu)^{b-1} \end{align} \] \(B(\boldsymbol \alpha,\beta)\)称为B函数，为一个标准化函数： \[ \begin{align} B(a,b) = \frac{\Gamma(a)\Gamma(b)}{\Gamma(a+b)} \end{align} \] 其目的是为了使整个概率分布积分等于1而存在的。Gamma函数的定义为： \[ \Gamma(x)=\int_0^{\infty}s^{x-1}e^{-s}\mathrm d s \] Gamma函数有一个性质：

\[ \Gamma(x+1)=x\Gamma(x) \] 证明为： \[ \begin{align*} \Gamma(x+1) &= \int_{0}^{\infty} {s^{x} e^{-s} ds} \\ &= \big[s^{x} (-e^{-s})\big] \big|_{0}^{\infty} - \int_{0}^{\infty} {(x s^{x-1}) (-e^{-s}) ds} \\ &= (0 - 0) + x \int_{0}^{\infty} {s^{x-1} e^{-s} ds} \\ &= x \Gamma(x) \end{align*} \]

除此之外：

\[ \Gamma(1)=1\\ \Gamma(\frac{1}{2})=\sqrt{\pi} \]

可以验证： \[ \int_0^1\text{Beta}(\mu|a,b)\mathrm d\mu=1 \]

Beta分布的均值和方差为：

\[ \mathbb E[\mu]=\frac{a}{a+b}\\ \text{var}[\mu]=\frac{ab}{(a+b)^2(a+b+1)} \]

因为后验分布与先验和似然函数的乘积成比例，那么： \[ p(\mu|m,l,a,b)\propto\mu^{m+a-1}(1-\mu)^{l+b-1} \]

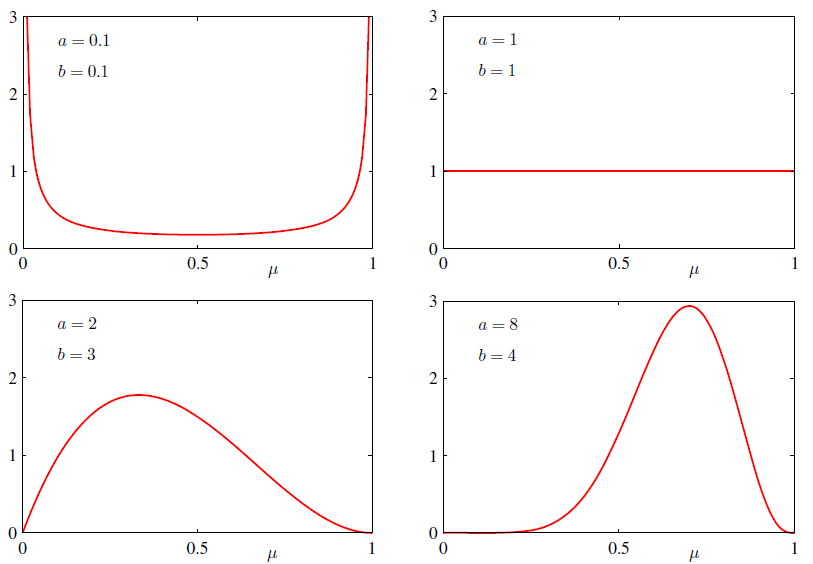
其中\(l=N-m\)。乘上标准化因子，就得到： \[ p(\mu|m,l,a,b)=\frac{\Gamma(m+a+l+b)}{\Gamma(m+a)\Gamma(l+b)}\mu^{m+a-1}(1-\mu)^{l+b-1} \] 得到的仍然是Beta分布，相当于把\(a\rightarrow{m+a}\)，\(b\rightarrow{l+b}\)。同时不难发现，参数\(a\)和\(b\)都有比较直观的意义。\(a\)可以看作是历史记录中，成功的次数，\(b\)可以看作是历史记录中失败的次数，比如\(a=2\)，\(b=3\)，根据经验成功的概率应该在\(\frac{2}{2+3}=0.4\)左右，即我们的先验为成功的概率为\(0.4\)（见下图左下角的子图）。如果在实验中，又进行了\(7\)次实验，其中\(m=6\)，\(l=1\)，由于成功的次数变多了，\(a=2+6=8\)，\(b=3+1=4\)，直觉上来说我们对成功概率的估计应当相应提高，大概为\(\frac{8}{8+4}\approx 0.67\)左右。这时的Beta分布如右下角的图的样子，也印证了我们的直觉。

以下为不同参数对应的Beta分布的互动演示：

最后，Beta还有一个有趣的应用就是，如果我们不断接收到新的观测数据，那么旧的后验分布则可以作为新的先验分布将参数更新下去 。这相当于说，基于已有的观测数据，我们提出一个先验Beta分布，然后根据新得到的一批观测数据，用先验Beta分布计算一个似然函数，将似然函数和先验Beta分布乘起来，归一化后得到了新的后验分布，只要不断有新的观测数据接收到，就可以把后验分布作为新的先验，不断更新下去。这样做的优势是对于大数据集，我们不需要整个数据集，而是只需要一批一批的更新即可。

Probability Distributions for Multinomial Variables

Intro

前面我们讨论了二值随机变量，现在我们将其扩展到多值变量。设一个\(K\)维向量\(\mathbf x\)，当\(x_k\)为\(1\)的时候其他元素都为\(0\)，如\(K=6,x_3=1\)时\(\mathbf x\)表示为\(\mathbf x=(0,0,1,0,0,0)^\top\)。如果\(p(x_k=1)=\mu_k\)，那么\(\mathbf x\)的概率分布为： \[ p(\mathbf x|\boldsymbol \mu)=\prod_{k=1}^{K}\mu_k^{x_k} \] \(\mu_k\)满足\(\sum_k \mu_k=1\)和\(\mu_k\geqslant 0\)，该分布被称作是Categorical Distribution。易知其均值为： \[ \begin{align} \mathbb E[\mathbf x|\boldsymbol \mu]=\sum_{\mathbf x}p(\mathbf x|\boldsymbol \mu)\mathbf x=\boldsymbol \mu \end{align} \] 假设我们有大小为\(N\)的数据集\(\mathcal D\)，每个样本服从该分布且相互独立，那么似然函数： \[ p(\mathcal D|\boldsymbol \mu)=\prod_{n=1}^N\prod_{k=1}^K \mu_k^{x_{nk}}=\prod_{k=1}^K \mu_k^{\sum_n x_{nk}}=\prod_{k=1}^K\mu_k^{m_k} \] 其中\(m_k=\sum_n x_{nk}\)，即\(x_k=1\)的数量。为了最大化对数似然同时保证\(\sum_k \mu_k=1\)，我们可以用拉格朗日乘子法： \[ \sum_{k=1}^K m_k\ln \mu_k+\lambda\left(\sum_{k=1}^K\mu_k-1\right) \] 我们得到\(\mu_k=-m_k/\lambda\)。通过\(\sum_k \mu_k=1\)得出\(\lambda=-N\)，故最后我们有： \[ \mu_k^{ML}=\frac{m_k}{N} \]

这相当于是\(x_k=1\)的数量除以总数。

Multinomial Distribution

类似的，我们可以对多次实验进行建模，假设进行\(N\)次独立实验，概率分布可以写为：

\[ \text{Mult}(m_1,m_2,\cdots,m_K|\boldsymbol\mu,N)=\binom{N}{m_1m_2\cdots m_K}\prod_{k=1}^K\mu_k^{m_k} \]

这也是我们熟知的多项分布 (Multinomial Distribution)，其中\(\binom{N}{m_1m_2\cdots m_K}\)为正则化因子： \[ \binom{N}{m_1m_2\cdots m_K}=\frac{N!}{m_1!m_2!\cdots m_K!} \] 注意\(\sum\limits_{k=1}^K m_k=N\)。

Dirichlet Distribution

有了前面Beta的启发，我们同样可以对多项分布的参数\(\mu_k\)建立共轭先验。首先根据似然函数，我们知道先验应当与\(\mu_k\)的幂的乘积成比例：

\[ p(\boldsymbol \mu|\boldsymbol \alpha) \propto \prod_{k=1}^{K}\mu_k^{a_{k-1}} \]

其中\(0\leqslant \mu_k\leqslant 1\)且\(\sum_k\mu_k=1\)。和Beta分布不同，由于要满足\(\sum\mu_k=1\)，所以\(\{\mu_k\}\)的取值会位于\(K-1\)的单纯型上，如下图所示：

加上标准化因子，我们就得到了所谓的先验分布，称之为迪利克雷分布 (Dirichlet Distribution)： \[ \text{Dir}(\boldsymbol \mu|\boldsymbol\alpha)=\frac{\Gamma(\alpha_0)}{\Gamma(\alpha_1)\cdots\Gamma(\alpha_K)}\prod_{k=1}^K\mu_k^{a_{k-1}} \]

其中\(\Gamma(\cdot)\)为Gamma函数，\(\alpha_0=\sum\limits_{k=1}^K\alpha_k\)。下图为不同条件下的迪利克雷分布的可视化：

\(\boldsymbol \mu\)的后验与先验和似然函数的乘积成正比：

\[ p(\boldsymbol\mu|\mathcal D,\boldsymbol\alpha)\propto p(\mathcal D|\boldsymbol\mu)p(\boldsymbol\mu|\boldsymbol\alpha)\propto\prod_{k=1}^K \mu_k^{\alpha_k+m_k-1} \]

不难验证：

\[ \begin{align} p(\boldsymbol\mu|\mathcal D,\boldsymbol\alpha) &= \text{Dir}(\boldsymbol\mu|\boldsymbol\alpha+\mathbf m)\\ &=\frac{\Gamma(\alpha_0+N)}{\Gamma(\alpha_1+m_1)\cdots\Gamma(\alpha_K+m_K)}\prod_{k=1}^K\mu_k^{\alpha_k+m_k-1} \end{align} \]

即后验同样为迪利克雷分布。