Deep Anomaly Detection Using Geometric Transformations

本文最后更新于：2 年前

Introduction

本文考虑图像数据的异常检测问题。与基于重构的方法不同，本文提出的方法通过对正常图片施加不同的几何变换之后，训练一个多分类器将无监督异常检测问题转化为一个有监督问题。本方法背后的直觉是在训练能够分辨不同变换后的图片之后，分类器一定学得了一些显著的几何特征，这些几何特征是正常类别独有的。

Proposed Method

Problem Statement

本文考虑针对图像的异常检测。记\(\mathcal X\)为所有自然图像的空间，\(X\subseteq\mathcal X\)为正常图像集合。给定数据集\(S\subseteq X\)，异常检测的目的是学习一个分类器\(h_S(x):\mathcal X\rightarrow\{0,1\}\)，其中\(h_S(x)=1\Leftrightarrow x\in X\)。

为了兼顾查准率和查全率，常用的设置是学习一个打分函数\(n_S(x):\mathcal X\rightarrow\mathbb R\)，分数越高代表样本属于\(X\)的概率越大。之后，通过设定阈值，便可以构建异常分类器： \[ \begin{align} h_S^\lambda(x)= \begin{cases} 1 & n_S(x)\leq\lambda\\ 0 & n_S(x)<\lambda \end{cases} \end{align} \]

Discriminative Learning of an Anomaly Scoring Function Using Geometric Transformations

有初始数据集\(S\)，几何变换集合\(\mathcal T\)，通过对\(S\)中每个样本施加这\(|\mathcal T|\)个几何变换得到新数据集记为\(S_\mathcal{T}\)，且\(S_\mathcal{T}\)中每个样本的标签为变换的序号。之后，在\(S_\mathcal{T}\)上训练一个\(|\mathcal T|\)分类器。在测试阶段，对测试样本同样施加\(|\mathcal T|\)个几何变换，分类器会给出经过\(\mathrm{softmax}\)的输出向量，最终的异常分数由经过输出的向量构造的分布对数似然得来。

Creating and Learning the Self-Labeled Dataset

设\(\mathcal T=\{T_0,T_1,\cdots,T_{k-1}\}\)为几何变换集合，\(1\leq i\leq k-1,\space T_i:\mathcal X\rightarrow \mathcal X\)，且\(T_0(x)=x\)。\(S_\mathcal{T}\)定义为：

\[ S_\mathcal T=\{(T_j(x),j):x\in S,T_j\in\mathcal T\} \] 对于每个\(x\in S\)，\(j\)为\(T_j(x)\)的标签。我们直接学习一个\(K\)类分类器\(f_\theta\)，来预测输入样本对应的几何变换种类，这相当于是一个图像分类问题。

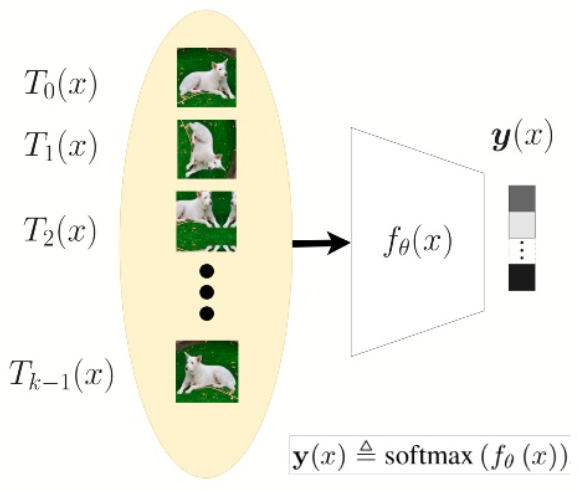
Dirichlet Normality Score

接下来要做的是如何定义异常分数，记为\(n_S(x)\)，这是文中的一个重要的部分。设几何变换集合\(\mathcal T=\{T_0,T_1,\cdots,T_{k-1}\}\)，且\(k\)分类器\(f_\theta\)在\(S_\mathcal{T}\)上完成训练。对于任意一个样本\(x\)，令\(\mathbf y(x)=\text{softmax}(f_{\theta}(x))\)，即分类器\(f_\theta\)输出的\(\text{softmax}\)之后的向量。异常分数\(n_S(x)\)定义为：

\[ n_S(x)=\sum\limits_{i=0}^{k-1}\log p(\mathbf y(T_i(x))|T_i) \]

该异常分数定义为每个类别上，在几何变换\(T_i\)的条件下，输出的\(\mathbf y\)的对数似然之和。在文中，作者假设\(\mathbf y(T_i(x)|T_i\)服从迪利克雷分布：\(\mathbf y(T_i(x))|T_i\sim\text{Dir}(\boldsymbol \alpha_i)\)，其中\(\boldsymbol \alpha_i\in\mathbb R^k_+\)，\(x\sim p_X(x)\)，\(i\sim\text{Uni}(0,k-1)\)，而\(p_X(x)\)代表正常样本的真实数据分布。于是：

\[ n_S(x)=\sum_{i=0}^{k-1}\left[\log\Gamma(\sum_{j=0}^{k-1}[\tilde{\boldsymbol\alpha}_i]_j)-\sum_{j=0}^{k-1}\log\Gamma([\tilde{\boldsymbol\alpha}_i]_j)+\sum_{j=0}^{k-1}([\tilde{\boldsymbol\alpha}_i]_j-1)\log\mathbf y(T_i(x))_j\right] \]

因为\(\tilde{\alpha}_i\)相对于\(x\)来说是常数，所以可以直接忽略，于是式子简化为： \[ n_S(x)=\sum_{i=0}^{k-1}\sum_{j=0}^{k-1}([\tilde{\boldsymbol\alpha}_i]_j-1)\log\mathbf y(T_i(x))_j=\sum_{i=0}^{k-1}(\tilde{\boldsymbol \alpha}_i-1)\cdot\log\mathbf y(T_i(x)) \]

注意这里的每个\(\boldsymbol \alpha_i\)都是一个向量，即对于每个变换\(i\)，都对应一个迪利克雷分布，其参数为\(\boldsymbol\alpha_i\)；在对训练集进行第\(i\)个几何变换之后，我们得到了\(\{T_i(x)\}\)，然后分类器\(f_\theta(\cdot)\)的输出\(\mathbf y(T_i(x))\)相当于迪利克雷分布的观测值，我们需要根据观测值来估计参数\(\boldsymbol \alpha_i\)，然后根据这个参数来计算\(n_S(x)\)。对于\(\boldsymbol\alpha_i\)，可以知道其第\(i\)个分量应该是相对比较大的，下面是运行官方代码得到的\(\boldsymbol\alpha_i\)的结果（\(i=69\)，\(i\)从\(0\)开始，总共为\(72\)维），可以看到第\(69\)个分量是最大的。

1
2
3
4
5
6
7
8
9
10
11
12
13
[INFO] value of mle_alpha_t:
 [ 0.10228925  0.08997199  0.13083569  0.10862965  0.09811163  0.08527119
  0.17637901  0.27628416  0.12873376  0.19197053  0.11587154  0.09873095
  0.12700618  0.07688542  0.10488203  0.12499191  0.11637607  0.07739511
  0.13049147  0.51031647  0.20546597  0.15558449  0.09288609  0.12134945
  0.09324992  0.14650162  0.16281216  0.11827823  0.08214853  0.15618336
  0.28129761  0.45293697  0.11485838  1.78598954  0.16556983  0.1141158
  0.10909459  0.13916602  0.11563799  0.07309986  0.11049714  0.12974086
  0.15930642  0.13714361  0.13938356  0.70619553  0.11174039  0.07201538
  0.16626109  0.12153727  0.09548811  0.07940956  0.15832209  0.11035474
  0.12487912  0.16937875  0.23212662  0.37041831  0.08557451  0.0839439
  0.09924258  0.39766872  0.14917286  0.08704662  0.09554555  0.31047109
  0.24504759  0.16812463  0.11508187 63.98878807  0.12971073  0.07972932]

下图也展示了对于每个变换\(i\)，\(\mathbf y(T_i(x)|T_i\)分布的情况：

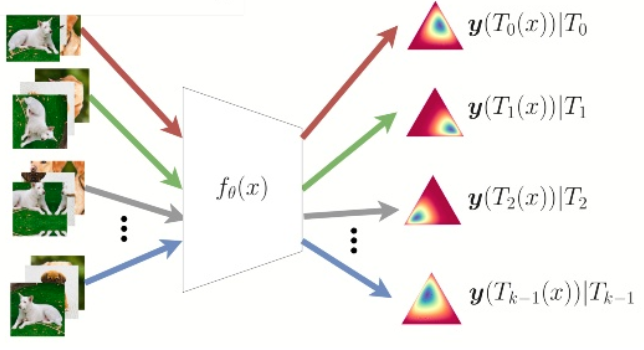
作者还给出了一种简化的形式，\(\hat{n}_S(x)=\frac{1}{k}\sum^{k-1}_{j=0}[\mathbf y(T_j(x))]_j\)。相当于说，对于每个变换\(T_i\)分类器都会给出一个\(\text{softmax}\)向量，取其第\(i\)个分量\([\mathbf y(T_j(x))]_j\)，然后把每个变换对应的\([\mathbf y(T_j(x))]_j\)加起来。

整个算法的流程如下：

这里结合作者的源代码简单说一下检测阶段的流程。

1
2
for t_ind in range(transformer.n_transforms):
        observed_dirichlet = mdl.predict(transformer.transform_batch(observed_data, [t_ind] * len(observed_data)), batch_size=1024)

在训练好模型之后，对于训练集的所有样本，对其进行\(K\)个几何变换之后，得到\(K\)个样本\(\{T_i(x)\}\)，对于所有第\(i\)个几何变换对应的样本\(\{T_i(x)\}\)，通过分类器\(f_\theta\)会给出输出\(\mathbf y(T_i(x))\)。这里对应算法中的第\(7-8\)行，这个observed_dirichlet就是\(S_i\)。

1
2
3
4
log_p_hat_train = np.log(observed_dirichlet).mean(axis=0)

alpha_sum_approx = calc_approx_alpha_sum(observed_dirichlet)
alpha_0 = observed_dirichlet.mean(axis=0) * alpha_sum_approx

之后这部分主要对应算法中的\(9-11\)行。作者把所有的第\(i\)个变换，分类器的输出的集合（也就是变量observed_dirichlet）记为\(S_i\)，\(\bar s\)为\(S_i\)的平均，\(\bar l\)为\(S_i\)对数的平均（变量log_p_hat_train），初始值\(\tilde{\alpha}_i\)由\(\bar s\frac{(k-1)(-\Psi(1))}{\bar s\cdot\log\bar s-\bar s\cdot\bar l}\)给出（变量alpha_0）。函数calc_approx_alpha_sum实现的是算法中第\(11\)行的\(\frac{(k-1)(-\Psi(1))}{\bar s\cdot\log\bar s-\bar s\cdot\bar l}\)，代码如下：

1
2
3
4
5
6
def calc_approx_alpha_sum(observations):
    N = len(observations)
    f = np.mean(observations, axis=0)

    return (N * (len(f) - 1) * (-psi(1))) / (
        N * np.sum(f * np.log(f)) - np.sum(f * np.sum(np.log(observations), axis=0)))
1
mle_alpha_t = fixed_point_dirichlet_mle(alpha_0, log_p_hat_train)

这里对应算法中的\(12-14\)行，即重复\(\tilde\alpha_i\leftarrow\Psi^{-1}\left(\Psi(\sum_j[\alpha_i]_j)+\bar l\right)\)来估计\(\alpha\)，函数fixed_point_dirichlet_mle代码如下：

1
2
3
4
5
6
7
8
def fixed_point_dirichlet_mle(alpha_init, log_p_hat, max_iter=1000):
    alpha_new = alpha_old = alpha_init
    for _ in range(max_iter):
        alpha_new = inv_psi(psi(np.sum(alpha_old)) + log_p_hat)
        if np.sqrt(np.sum((alpha_old - alpha_new) ** 2)) < 1e-9:
            break
        alpha_old = alpha_new
    return alpha_new

\(\Psi^{-1}(\cdot)\)是通过数值方法来估计的：

1
2
3
4
5
6
7
8
def inv_psi(y, iters=5):
    # initial estimate
    cond = y >= -2.22
    x = cond * (np.exp(y) + 0.5) + (1 - cond) * -1 / (y - psi(1))

    for _ in range(iters):
        x = x - (psi(x) - y) / polygamma(1, x)
    return x

最后，在得到对\(\alpha\)的估计之后，可以来计算测试样本的分数了。这里对应的是算法中的第\(16\)行。

1
2
3
x_test_p = mdl.predict(transformer.transform_batch(x_test, [t_ind] * len(x_test)), batch_size=1024)

scores += dirichlet_normality_score(mle_alpha_t, x_test_p)

函数dirichlet_normality_score代码如下：

1
2
def dirichlet_normality_score(alpha, p):
    return np.sum((alpha - 1) * np.log(p), axis=-1)

Experiments

Baselines

文中用到了如下的Baseline：

  • One-class SVM. 单类支持向量机，作者使用了三个变体，分别为RAW-OC-SVM——使用原始数据作为输入，CAE-OC-SVM——使用一个卷积自编码器来获得低维表示作为输入和E2E-OC-SVM——全名为One-Class Deep Support Vector Data Description；
  • Deep structured energy-based models.
  • Deep Autoencoding Gaussian Mixture Model.
  • Generative Adversarial Networks.

Datasets

文中用到了一下几个数据集：

  • CIFAR-10
  • CIFAR-100
  • Fashion-MNIST
  • CatsVsDogs

在实验中所有图片都被归一化到\([-1,1]\)的范围。

Experimental Protocol

设数据集有\(C\)个类，我们会进行\(C\)次实验，在第\(c\)次实验 (\(1\leq c \leq C\))中我们会将第\(c\)个类作为正常样本，而其他类作为异常样本。在训练阶段，训练集只包含正常样本，而在测试阶段则会有正常样本和异常样本。在获得异常分数之后，阈值\(\lambda\)则根据ROC曲线下面积选择。

实验中使用的几何变换基于以下三种基变换：

  • Horizontal flip: 记为\(T_b^{flip}(x)\)，\(b\in\{T,F\}\)代表是否翻转；
  • Translation: 记为\(T_{s_h,s_w}^{trans}(x)\)，其中\(s_h,s_w\in\{-1,0,1\}\)。在长宽两个维度上位移分别为\(0.25\)高度和\(0.25\)宽度，这两个维度发生位移的方向由\(s_h\)和\(s_w\)决定，当\(s_h=s_w=0\)时代表不移动；
  • Rotation by multiples 90 degrees: 记为\(T_k^{rot}(x)\)，\(k\in\{0,1,2,3\}\)。旋转\(k\times90\)度。

将三种基变换叠加有： \[ \mathcal T=\left\{ T_k^{rot}\circ T_{s_h,s_w}^{trans}\circ T_b^{flip} : \begin{matrix} b &\in \{T,F\}\\ s_h,s_w&\in\{-1,0,1\}\\ k&\in\{0,1,2,3\} \end{matrix} \right\} \] 最终几何变换种数为\(2\times3\times3\times4=72\)种。

分类器模型使用的是Wide Residual Network，优化器为Adam，Batch size为128，训练轮数为200。

Results

下面是不同方法在不同数据集上的实验结果：

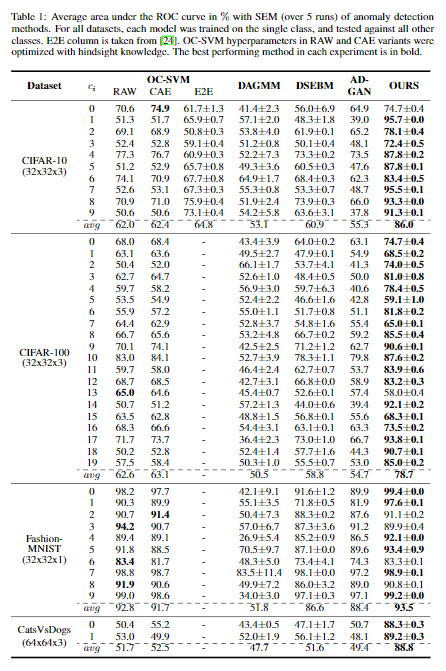
评测标准使用的是AUROC。作者关于结果的分析主要有以下几点：

  1. 在绝大多数情况下，我们的算法都比Baseline要好，而且是越大的数据集效果越好。CatsVsDogs数据集每张图片的大小比其他几个数据集都要大，而Baseline在这个数据集上的结果都在\(50\%\)或不到\(50\%\)，这基本等同于瞎猜；
  2. 在CIFAR-100数据集里，由于将这100类聚合为了20类，所以存在类内样本差异大的问题。比如在类\(5\)、类\(7\)和类\(13\)上，模型表现就不够好；
  3. 在Fashion-MNIST数据集上几乎所有方法（除了DAGMM）都表现很好。

On the Intuition for Using Geometric Transformations

这里作者对所选用的几何变换做了一些解释。实验中选用的三种基本几何变换都是可逆的线性几何变换（且为双射），作者也试过一些复杂的非线性变换，如高斯模糊、锐化、伽马校正等等，但是效果并不好。

作者认为分类器能够分辨不同变换的能力与最终性能成正比，为了验证这一点，进行了\(3\)个实验。从MNIST数据集选择一个数字作为正常样本，几何变换只采用两个，然后选择另一个数字作为异常样本，结果如下：

  • Normal digit: 8，Anomaly: 3，Transformations: Identity and horizontal flip. 由于数字\(8\)是对称的，所以要让分类器分辨原始的\(8\)和翻转之后的\(8\)是很难的，AUROC只有\(0.646\)；
  • Normal digit: 3，Anomaly: 8，Transformations: Identity and horizontal flip. 这里把\(3\)作为正常样本，由于\(3\)不是对称的，所以两种变换是可以分辨的，AUROC达到了\(0.957\)；
  • Normal digit: 8，Anomaly: 3，Transformations: Identity and translation by 7 pixels. 同样是把\(8\)作为正常样本，但变换用的是平移，AUROC达到了\(0.919\)。

除此之外，作者还设计了一个实验，目的是测试什么样的图像会获得较高的分数\(n_S(x)\)。在给定训练好的分类器的情况下，优化输入的图像，目标函数是最大化分数\(n_S(x)\)。下图为实验结果：

在左图中，将数字\(3\)作为正常样本训练的分类器、原始输入为数字\(0\)的图片时，随着优化的进行，图片慢慢地变得像数字\(3\)。在右图中，同样是将数字\(3\)作为正常样本训练的分类器，不过原始输入也是数字\(3\)，这时图像却没有怎么变化。

Remark

  • 文中提到的在CIFAR100数据的实验上，由于类间差异比较大导致效果较差，那么很自然地，不同的变换样本对应的集簇实际上应当足够分开，集簇内的样本要足够进，这样对于分类器来说才能比较好的分类。不过采用的几何变换并没有针对这一点进行特别设计；
  • 文中强调了所使用的变换为几何变换，其实除此之外，所使用的变换还都是可以用矩阵表示的可逆的变换。