Learning Representations of Ultrahigh-dimensional Data for Random Distance-based Outlier Detection
本文最后更新于:2 年前
Introduction
本文提出了一种针对高维数据异常检测的表示学习方法。文中提出了RAMODO框架,一种基于排序的结合表示学习和异常检测的无监督框架。除此之外,基于RAMODO,文中还提出了基于此框架的模型REPEN。
Proposed Method
The Proposed Framework: RAMODO
Problem Statement
我们的目的是为高维数据学习低维表示,同时在学到的低维表示中能够更好地进行异常检测。设有数据集\(\mathcal{X}=\{\mathbf x_1,\mathbf x_2,\cdots, \mathbf x_N\}\) (\(\mathbf x_i\in \mathbb{R}^D\)) 和一个基于随机距离的异常检测器\(\phi:\mathcal{X}\mapsto \mathbb{R}\),我们的目标是学习一个表示函数\(f:\mathcal{X}\mapsto\mathbb{R}^M (M\ll D)\)使得对于所有异常样本\(\mathbf x_i\)和正常样本\(\mathbf x_j\)都有\(\phi(f(\mathbf x_i))>\phi(f(\mathbf x_j))\)。
Ranking Model-based Representation Learning Framework
RAMODO基于pairwise ranking model。第一步是通过一定的预处理算法(原文中称为outlier thresholding)将数据划分为inlier候选集和outlier候选集;第二步通过随机从inlier候选集采样\(n\)个样本生成query set \((\mathbf x_i,\cdots,\mathbf x_{i+n-1})\),从inlier候选集采样一个样本生成positive example \((\mathbf x^+)\),从outlier候选集采样一个样本生成negative example \((\mathbf x^-)\),将三者组合生成 metatriplet \(T=(<\mathbf x_i,\cdots,\mathbf x_{i+n-1}>,\mathbf x^+,\mathbf x^-)\);第三步通过神经网络\(f\)学习表示;第四步通过outlier score-based ranking loss \(L(\phi(f(\mathbf x^+)|<f(\mathbf x_i),\cdots,f(\mathbf x_{i+n-1})>),\phi(f(\mathbf x^-)|<f(\mathbf x_i),\cdots,f(\mathbf x_{i+n-1})>))\)来进行优化,其中\(\phi(\cdot|\cdot)\)为基于距离的异常检测器。
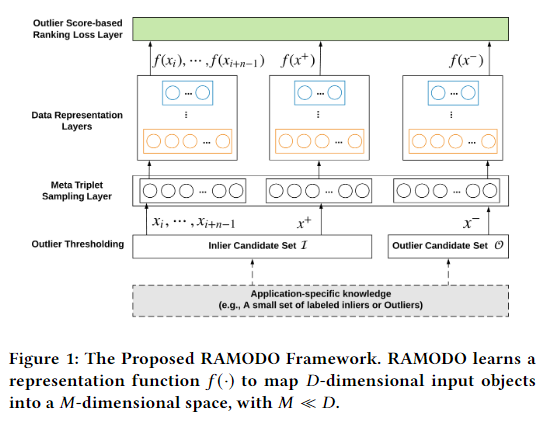
A RAMODO Instance: REPEN
REPEN为RAMODO的实例模型,使用Sp作为异常检测器。
Outlier Thresholding Using State-of-the-art Detectors and Cantelli's Inequality
第一步使用Sp作为基础获得初始anomaly score:
Definition 1 (Sp-based Outlier Scoring). 给定样本\(x_i\),Sp 以以下方式定义该样本的异常程度: \[ r_i=\frac{1}{m}\sum\limits_{j=1}^m nn\_dist(\mathbf x_i|\mathcal{S}_j) \] 其中\(\mathcal S_j\subset \mathcal X\)为数据集随机采样的子集,\(m\)为集成大小,\(nn_dist(\cdot|\cdot)\)为\(\mathcal S_j\)中最近邻居的距离。
接着通过Cantelli's Inequality来定义Pseudo Outlier:
Definition 2 (Cantelli's Inequality-based Outlier Thresholding). 给定异常分数向量\(\mathbf r\in\mathbb R^N\),更高异常分数代表更高的可能性为异常,设\(\mu\)和\(\delta^2\)分别为均值和方差,Outlier候选集由以下方式确定: \[ \mathcal{O}=\{\mathbf x_i|r_i \geq \mu + \alpha\delta\}, \space\forall \mathbf x_i\in\mathcal X, \space r_i\in\mathbf r \] 其中\(\alpha\geq 0\)为自定义的阈值。
Inlier候选集\(\mathcal I=\mathcal X\backslash \mathcal O\)。
Triplet Sampling Based on Outlier Scores
首先,从\(\mathcal I\)采样一定数量的样本组成query set,每个样本被采样的概率与其对应的异常分数有关:
\[ p(\mathbf x_i)=\frac{\mathbb Z-r_i}{\sum_{t=1}^{|\mathcal I|}[\mathbb Z-r_t]} \]
其中\(\mathbb Z=\sum_{t=1}^{|\mathcal I|}r_t\)。
之后从inlier set中均匀随机采样一个positive sample \(\mathbf x^+\)。最后从outlier set中根据以下概率采样一个negative sample \(\mathbf x^-\): \[ p(\mathbf x_j)=\frac{r_j}{\sum_{t=1}^{|\mathcal O|}r_t} \]
A Shallow Data Representation
单层神经网络用来获得浅层的表示:
Definition 3 (Single-layer Fully-connected Representations) 给定输入\(x\), \[ f_\Theta(\mathbf x)=\{\psi(\mathbf w_1^\top\mathbf x),\psi(\mathbf w_2^\top\mathbf x),\cdots,\psi(\mathbf w_M^\top\mathbf x)\} \] 其中\(\psi(\cdot)\)为激活函数,\(\mathbf w\)为权重矩阵。
Ranking Loss Using Random Nearest Neighbor Distance-based Outlier Scores
设\(\mathcal{Q}=<f_\Theta(\mathbf x_i),\cdots,f_\Theta(\mathbf x_{i+n-1})>\)为query set,给定样本\(\mathbf x\),REPEN根据最近邻距离定义了\(f_\Theta(\mathbf x)\)的异常程度: \[ \phi(f_\Theta(\mathbf x)|\mathcal{Q})=nn\_dist(f_\Theta(\mathbf x)|\mathcal Q) \] 因此,给定三元组\(T=(\mathcal Q,f_\Theta(\mathbf x^+),f_\Theta(\mathbf x^-))\),我们的目标是学得表示\(f(\cdot)\)使得: \[ nn\_dist(f_\Theta(\mathbf x^+)|\mathcal Q)<nn\_dist(f_\Theta(\mathbf x^-)|\mathcal Q) \] 损失函数: \[ J(\Theta;T)=L(\phi(f_\Theta(\mathbf x^+)|\mathcal Q),\phi(f_\Theta(\mathbf x^-)|\mathcal Q))=\\\max\{0, c+nn\_dist(f_\Theta(\mathbf x^+)|\mathcal Q)-nn\_dist(f_\Theta(\mathbf x^-)|\mathcal Q)\} \] 其中\(c\)为边界参数。给定一系列三元组,最终优化目标如下: \[ \mathop{\text{arg min}}\limits_{\Theta}\frac{1}{|\mathcal{T}|}\sum\limits_{i=1}^{|\mathcal T|}J(\Theta;T_i) \]
The Algorithm and Its Time Complexity

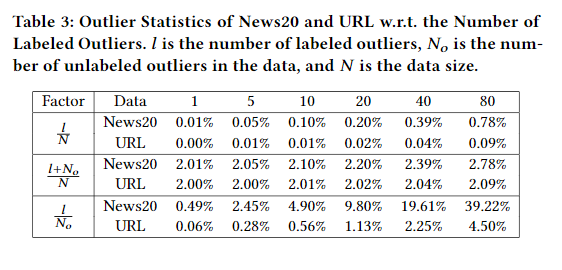
Leveraging A Few Labeled Outliers to Improve Triplet Sampling
Experiments
Datasets
- AD:网络广告检测
- LC:肺癌疾病监测
- p53:异常蛋白质活动检测
- R8:文本分类
- News20:文本分类
- URL:异常网址检测
- Webspam:Pascal Large Scale LearningChallenge
Effectiveness in Real-world Data with Thousands to Millions of Features
作者分别使用原始特征和REPEN学到的特征进行异常检测,IMP代表性能提升比例,SU代表加速比例。
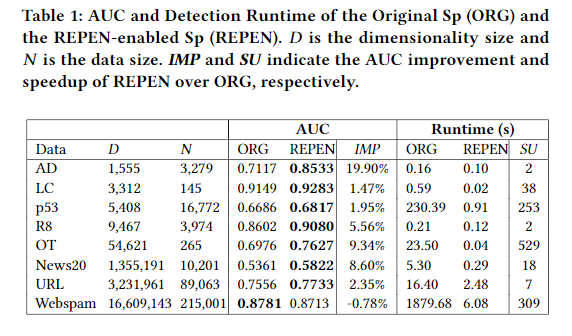
Comparing to State-of-the-art Representation Learning Competitors
- AE: 自编码器
- HLLE: Hessian Locally Linear Embedding
- SRP: Sparse Random Projection
- CoP: Coherent Pursuit
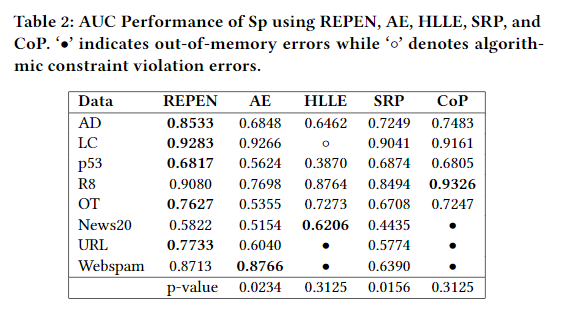
The Capability of Leveraging Labeled Outliers as Prior Knowledge
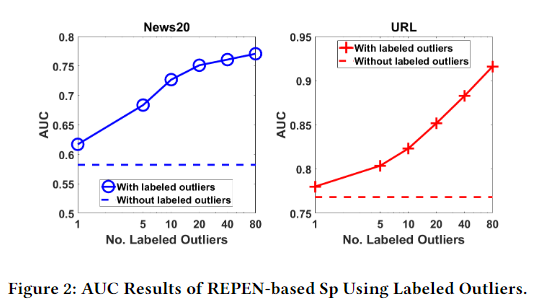
Sensitivity Test w.r.t. the Representation Dimension
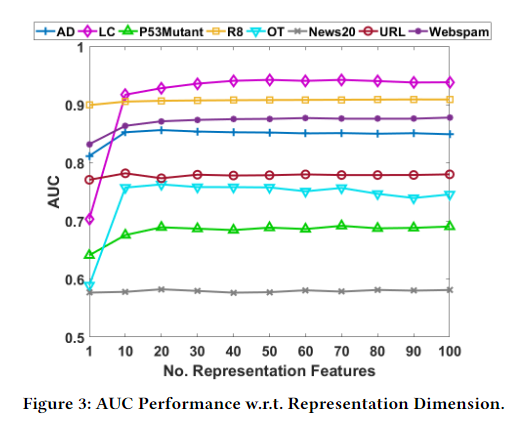
文中提到了对于R8、URL、News20这三个数据集在维度\(M=1\)的时候表现和其他维度一样好,作者给出的解释是在这几个数据集中异常部分是线性可分的,所以1维就足够了,另一个解释是优化问题。
Scalability Test
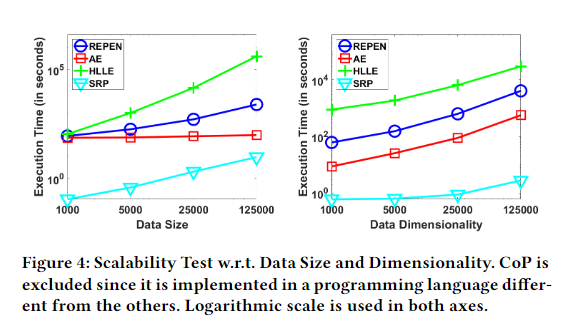
本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!