本文最后更新于：2 年前

Introduction

在文献中，因为标注成本的昂贵，无监督方法占据了异常检测的主要位置。然而，在现实生活中，我们可能会有少量标签，如何利用这部分标签信息就成为了一个问题，作者将其称之为anomaly-informed modeling。作者提出了两点挑战：

少量标签可能无法提供所有类型异常的信息；
大部分无标签数据为正常样本，但其中包含少部分异常（污染）。

作者提出了基于pairwise relation learning的方法来解决这些问题。文章的主要贡献如下：

提出了一种基于pairing-based data augmentation和ordinal regression来进行弱监督异常检测的框架
基于该框架提出了PReNet，一种基于双流ordinal regression的网络
从理论和实践角度分析了方法的有效性
在40个真实数据集上进行了完善的实验

Proposed Method

Learning Anomaly Scores by Predicting Pairwise Relation

Problem Formulation

给定数据集\(\mathcal{X}=\{\mathbf{x}_1,\mathbf {x}_2,\cdots,\mathbf{x}_N,\mathbf{x}_{N+1},\cdots,\mathbf{x}_{N+K}\}\)，包含两部分，一部分是五标签数据\(\mathcal{U}=\{\mathbf{x}_1,\mathbf {x}_2,\cdots,\mathbf{x}_N\}\)，另一部分是有标签异常数据\(\mathcal{A}=\{\mathbf{x}_{N+1},\cdots,\mathbf{x}_{N+K}\}\)，其中\(K\ll N\)。我们的任务目标是学习一个打分函数\(\phi:\mathcal{X}\mapsto \mathbb{R}\)，使得对任任意异常样本的打分高于任意正常样本。

在这个Formulation里，作者将关系学习和异常打分统一了起来。首先，输入的数据集不再是原始样本，而是样本对。样本对包含三种：anomaly-anomaly，anomaly-unlabeled，unlabeled-unlabeled，记为\(C_{\{\mathbf{a},\mathbf{a}\}}\)，\(C_{\{\mathbf{a},\mathbf{u}\}}\)，\(C_{\{\mathbf{u},\mathbf{u}\}}\)。每一个样本对包含一个标签\(y\)，表示该pair对应的异常分数，整个输入数据集\(\mathcal{P}=\{\{\mathbf{x}_i,\mathbf{x}_j,y_{ij}\}|\mathbf{x}_i,\mathbf{x}_j\in\mathcal{X} \space\text{and}\space y_{ij}\in\mathbb{N}\}\)。因为有\(y_{\{\mathbf a,\mathbf a\}}>y_{\{\mathbf a,\mathbf u\}}>y_{\{\mathbf u,\mathbf u\}}\)，所以对关系的学习也是对异常打分的学习。

The Instantiated Model: PReNET

下图为模型示意图，Data Augmentation模块负责产生pair数据，End-to-End Anomaly Score Learner \(\phi\) 模块负责关系学习（异常打分）。

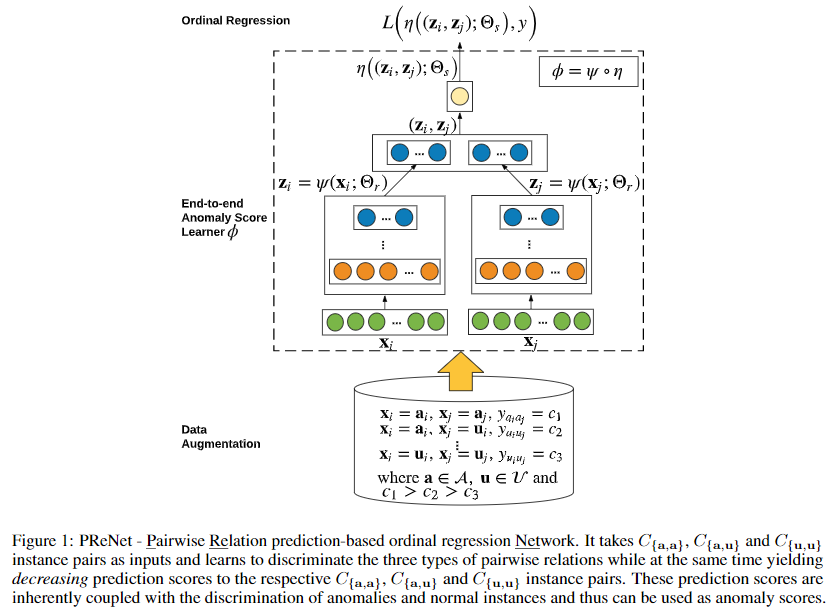
Data Argumentation by Pairing

数据的产生分为两步：

从\(\mathcal{A}\)和\(\mathcal{U}\)上随机采样，组成pair；
对每个pair打上次序(ordinal class feature) 标签\(\mathbf{y}\)。

部分\(C_{\{\mathbf{a},\mathbf{u}\}}\)和\(C_{\{\mathbf{u},\mathbf{u}\}}\)可能包含异常污染，因为在\(\mathcal{U}\)中可能会有未标记的异常样本。

End-to-End Anomaly Score Learner

令\(\mathcal{Z}\in\mathbb{R}^M\)为中间表示空间，那么Score Learner可以拆解为特征学习\(\psi(\cdot;\Theta_r):\mathcal{X}\mapsto \mathcal{Z}\)和打分函数\(\eta((\cdot,\cdot);\Theta_s):(\mathcal{Z},\mathcal{Z})\mapsto\mathbb{R}\)两部分，两部分都由神经网络组成。

Ordinal Regression

损失函数定义为： \[ L\left(\phi((\mathbf x_i,\mathbf x_j);\Theta),y_{ij}\right)=|y_{ij}-\phi((\mathbf x_i,\mathbf x_j);\Theta)| \] 采用绝对值而不是均方误差的原因是为了减少异常污染的影响。默认\(y_{\{\mathbf a,\mathbf a\}}=8\)，\(y_{\{\mathbf a,\mathbf u\}}=4\)，\(y_{\{\mathbf u,\mathbf u\}}=0\)。最后的优化函数可以写为： \[ \mathop{\text{argmin}}\limits_{\Theta}\frac{1}{|\mathcal{B}|}\sum\limits_{\{\mathbf x_i,\mathbf x_j, y_{ij}\}\in\mathcal{B}}|y_{ij}-\phi((\mathbf x_i,\mathbf x_j);\Theta)|+\lambda R(\Theta) \] \(\mathcal{B}\)为一个batch，\(R(\Theta)\)为正则项。

Anomaly Detection Using PReNet

Training Stage

训练流程如下图所示：

为了保证训练样本类别的平衡，\(\frac{|\mathcal{B}|}{2}\)的样本采样自\(C_{\{\mathbf u,\mathbf u\}}\)，采样自\(C_{\{\mathbf a,\mathbf u\}}\)和\[C_{\{\mathbf a,\mathbf a\}}\]的样本都占\(\frac{|\mathcal{B}|}{4}\)。

Anomaly Scoring Stage

在测试阶段，给定测试样本\(\mathbf{x}_k\)，先分别从\(\mathcal{A}\)和\(\mathcal{U}\)采样，然后定义以下anomaly score： \[ s_{\mathbf{x}_k}=\frac{1}{2E}\left[\sum\limits_{i=1}^E\phi((\mathbf a_i,\mathbf x_k);\Theta^*)+\sum\limits_{j=1}^E\phi((\mathbf x_k,\mathbf u_j);\Theta^*)\right] \] \(\mathbf a_i\)和\(\mathbf u_j\)为随机采样得到的异常样本和正常样本，采样大小\(E\)默认为30。

Experiments

实验部分主要是回答以下四个问题：

在有限的标签异常情况下，PReNet能否有效地检测已知和未知的异常；
在不同数量标签异常的情况下，PReNet的表现如何；
PReNet对异常污染的鲁棒性如何；
PReNet不同组件的重要性如何。

Datasets

实验一共用到了40个数据集，其中12个用来评测算法检测已知的异常的能力（如Table 2所示），28个用来评测算法检测未知的异常的能力（如Table 3所示）。

Competing Methods and Parameter Settings

用到的baseline有以下几个：

DevNet：同一作者在KDD2019提出的异常检测框架
Deep support vector data description (DSVDD)：深度支持向量数据描述
Prototypical network： few-shot classification中的一种模型
iForest：孤立森林

Performance Evaluation Metrics

用到的Metrics为AUC-ROC和AUC-PR。

Detection of Known Anomalies

在本实验中，异常污染的比例（2%）和有标记异常样本的数量（60）是固定的，下表为实验结果：

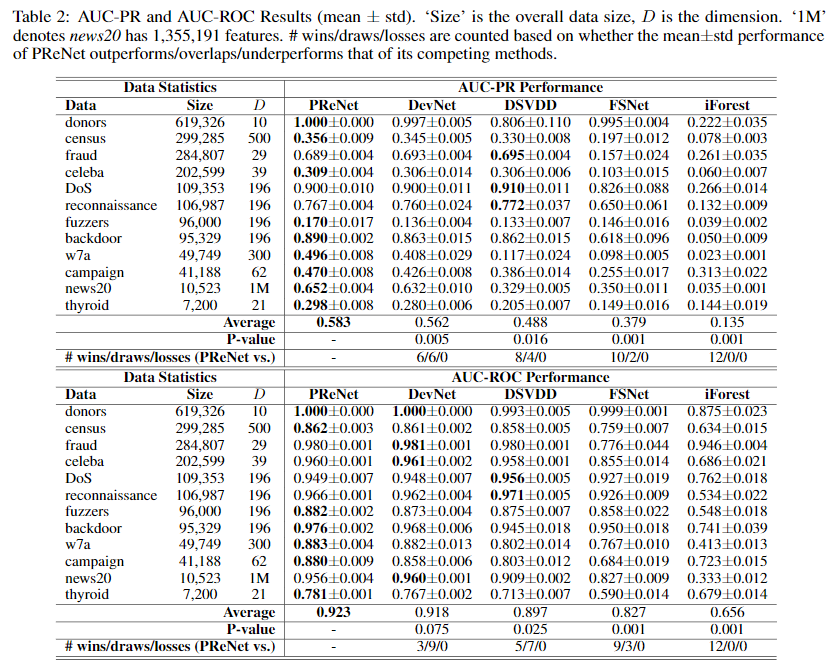
Detection of Unknown Anomalies

在本实验中，异常污染的比例（2%）和有标记异常样本的数量（60）同样是固定的，下表为实验结果：

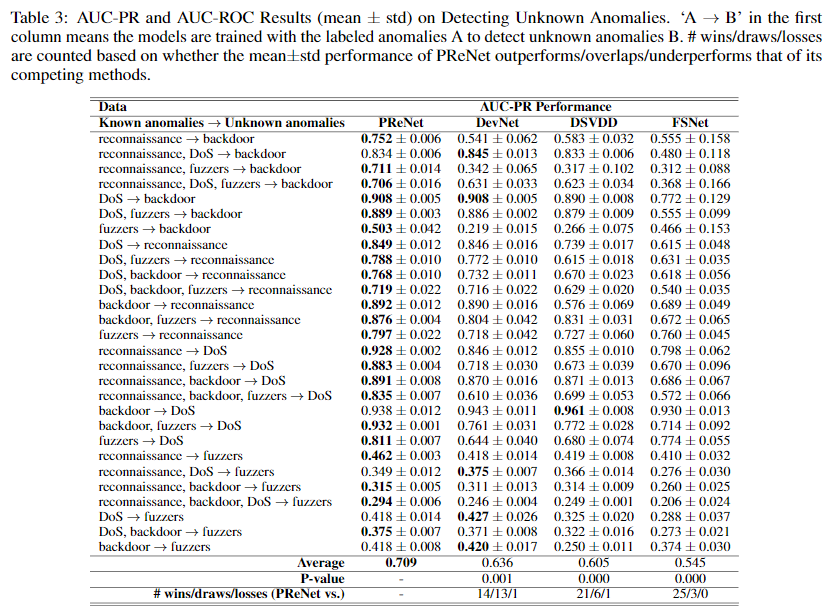
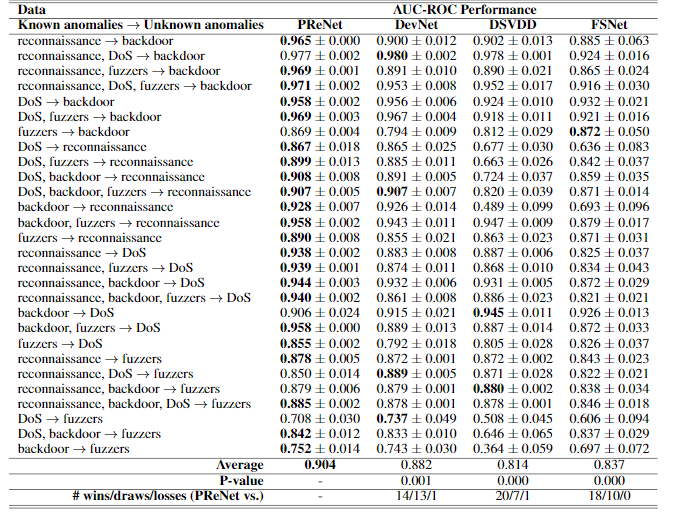
Availability of Known Anomalies

本实验主要是研究不同数量标注异常样本的条件下，算法的性能如何。异常污染的比例固定（2%），标注异常的数量从15到120变化。实验结果如下：

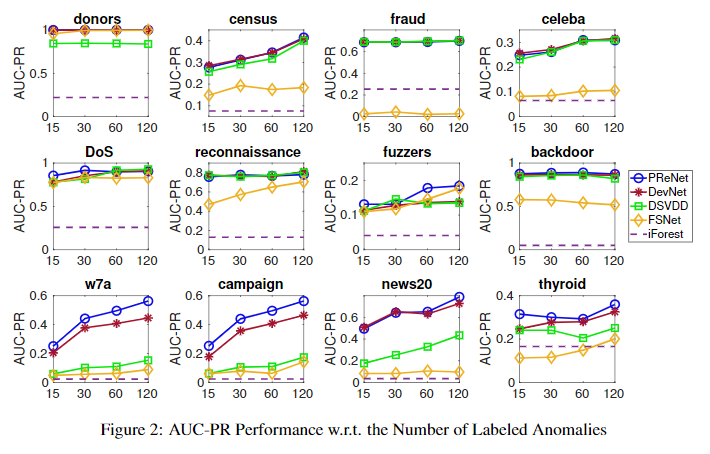
Further Analysis of PReNet

Tolerance to Anomaly Contamination in Unlabeled Data

本实验主要研究不同异常污染比例下，算法的性能，即探究算法对异常污染的鲁棒性。标注异常样本的数量恒定（60），异常污染比例在\(\{0\%,2\%,5\%,10\%\}\)中变化。实验结果如下所示：

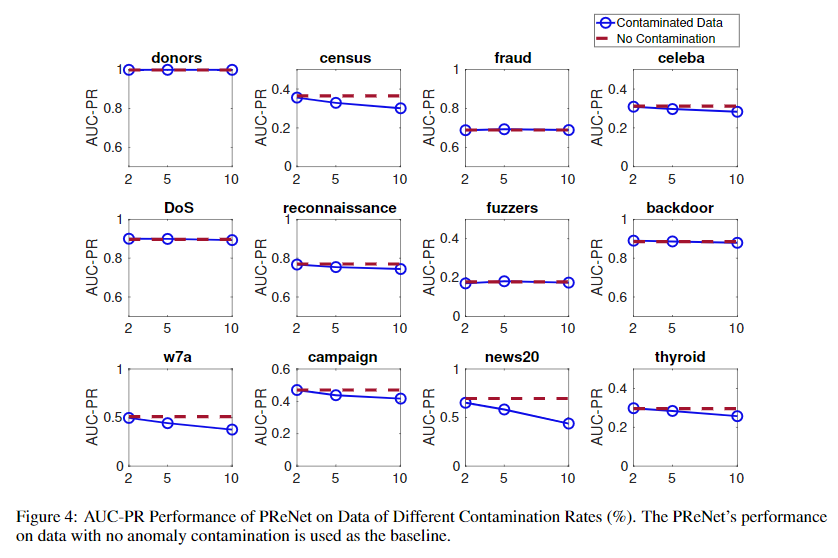
Ablation Study

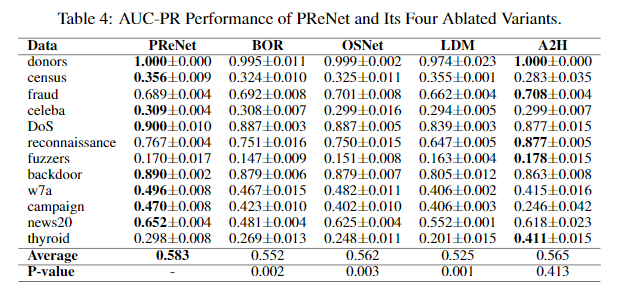
这一节是消融实验，分别设置了四个变体：

BOR: 损失函数替换成了二值回归Binary Ordinal Regression；
OSNet: 将双流结构简化为单流；
LDM: 将网络中的隐藏层去除；
A2H: 加入了额外的隐藏层，并且加入了\(\ell_2\)-norm防止过拟合。

Research Anomaly Detection

Anomaly Detection

本博客所有文章除特别声明外，均采用 CC BY-SA 4.0 协议，转载请注明出处！

Learning Representations of Ultrahigh-dimensional Data for Random Distance-based Outlier Detection 上一篇

Discovering Physical Concepts with Neural Networks 下一篇

Deep Weakly-supervised Anomaly Detection