Discovering Physical Concepts with Neural Networks

Introduction

如题目所示，本文的目的是利用神经网络来发掘物理概念。其思路是从实验数据学到表示，然后用学到的表示来回答物理问题，由此物理概念可以从学到的表示来提取出。作者进行了4个实验：

1. 在阻尼振动实验中，模型学到了相关的物理参数；
2. 在角动量守恒实验中，模型预测了质点的运动；
3. 给定量子系统的观测数据，模型正确的识别出了量子状态的自由度；
4. 给定从地球观测的太阳和火星的位置时间序列数据，模型发现了日心说模型。

Preliminaries

作者在附录中对神经网络的基础知识进行了介绍，这里不再赘述，只截取了一些相对前沿的内容。

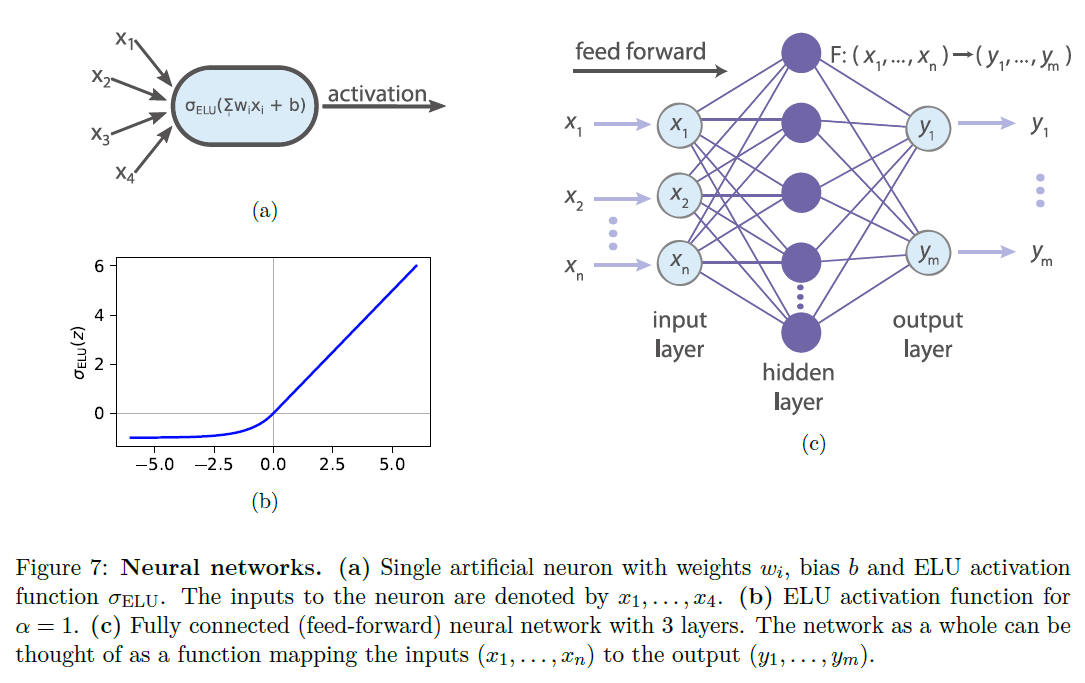
Variational Autoencoders

本文用到的模型基础是VAE：

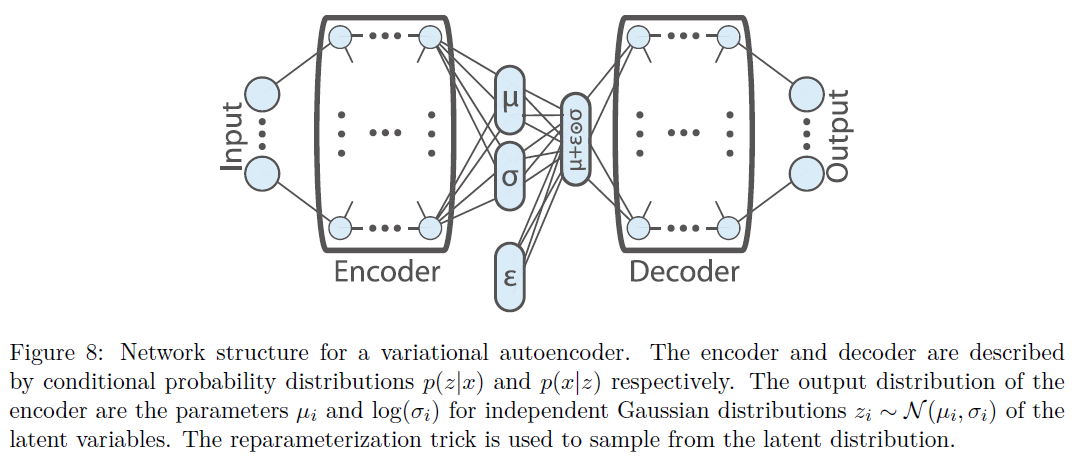
Representation Learning

Representation learning的主要目标是将数据映射到一个隐向量 (encoder)，为了保证隐向量包含了所有相关信息， 那么应该能够从隐向量还原原数据 (decoder)。传统的Autoencoder是这个思想的最简单实现，而VAE则将AE和Variational Inference结合了起来，是一种经典的生成式模型。现在很多研究关注Disentangled Representation Learning，也就是说我们希望模型能够无监督地学习数据，从中学到有意义的表示。

$$-VAE

$$-VAE是一种特殊的VAE，也是一个经典的Disentangled Representation Learning模型，它和VAE主要的区别是对KL散度一项加上了权重$$进行调节： $$ 如果假设$$，那么损失函数可以进行简化： $$

Network Structure

Network Structure: SciNet

模仿物理学家建模物理问题的过程，作者提出了SciNet，如下图所示：

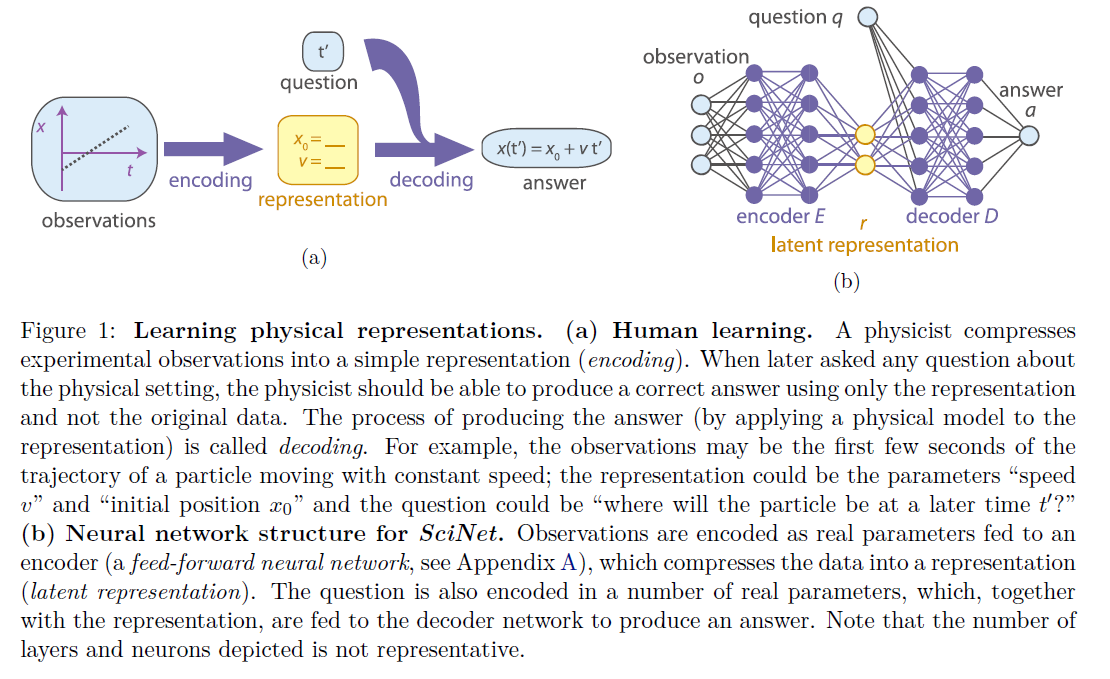
物理学家在建模物理问题的时候，往往是从一些实验数据出发，根据物理常识提取更加精练的表示，然后用学到的表示来回答物理问题。

对于单纯的输入输出问题，SciNet可以看作是一个映射，$$。$$是可能的实验数据集合，$$是可能的问题集合，$$是可能的答案集合。可以将其分为两个步骤：编码过程$$从实验数据学到表示，解码过程$$根据给定的问题从表示来回答问题。由此，$$。在实现方面，SciNet采用的是全连接网络。

Training and Testing SciNet

用来训练的数据形式为$$，观测$$和问题$$分别从观测集$$和问题集$$选出，$$为对应的正确答案。在训练过程中，我们希望准确度尽量高，并且学到minimal uncorrelated representations。为此，作者采用disentangling variational autoencoder作为模型。

Results

在文中，作者进行了4个实验来验证模型的有效性。

Damped Pendulum

阻尼振动实验：

• 任务：预测一维阻尼振动在不同时间的位置。

• 物理模型：$$，$$为弹性模量，$$为阻尼系数，通解为$$

• 观测数据：位置时间序列数据$$，时间间隔相等，质量$$，振幅$$，相位$$，弹性模量$$，阻尼系数$$。

• 问题：预测$$

隐变量大小设置为3，结果如下图所示：

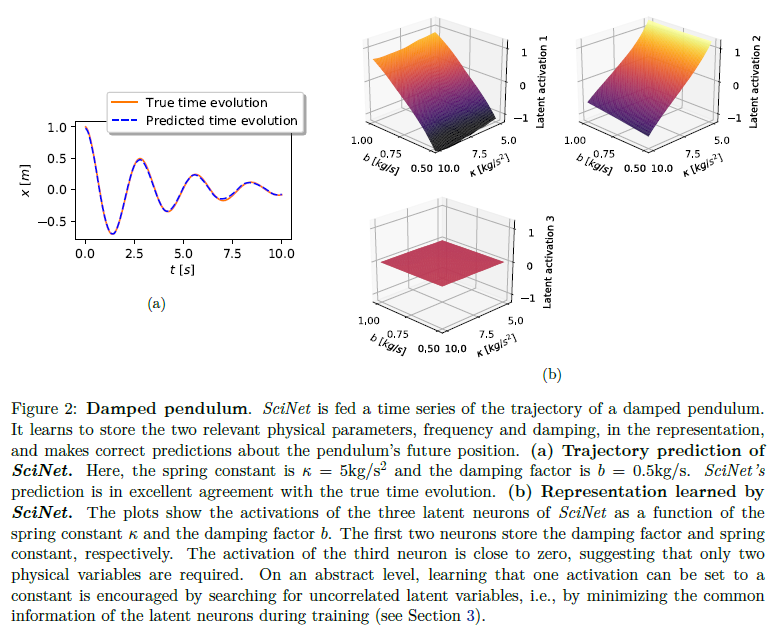
(b)中的三幅图分别是学到的三个隐变量和我们感兴趣的参数$$和$$的关系图。第一幅图中变量$$与$$几乎完全线性相关，与$$基于线性无关，变量$$只和$$相关。变量$$几乎为一个常数，故不提供额外的信息。由此作者认为SciNet学到了我们关心的两个参数的知识。

Conservation of Angular Momentum

角动量守恒实验：

• 任务：预测一个由长度为$$的绳子捆绑着的旋转质点在位置$$经一个自由质点撞击后的位置
• 物理模型：给定撞击之前的角动量，自由质点撞击之后的速度，旋转质点在撞击之后在时间$$的位置可以由角动量守恒定律给出：

$$

• 观测数据：在撞击之前两个质点的位置数据$$，质量为固定值，半径$$也为固定值。数据添加高斯噪声。
• 问题：预测撞击之后自由质点在时间$$的位置

实验室意图如下：

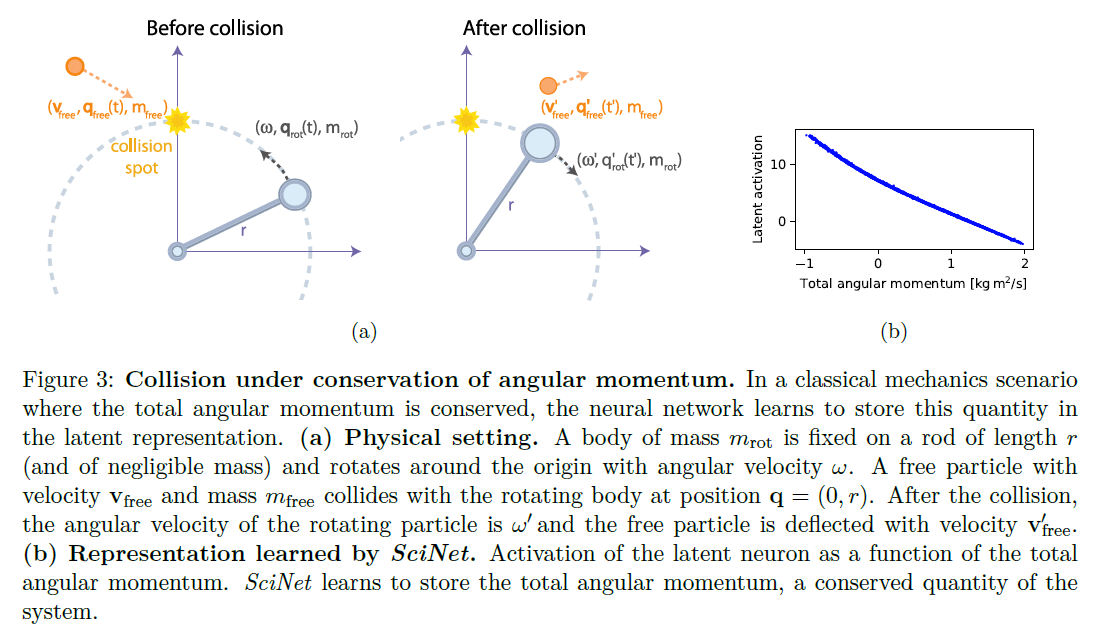
实验结果表明SciNet能够正确预测质点撞击之后的位置，同时对噪音鲁棒。根据(b)，隐变量和角动量存在线性相关关系，作者认为SciNet学到了守恒的动量这一概念。

Representation of Qubits

量子比特实验：

• 任务：预测在$$的纯$$量子位状态$$下任何二进制投影测量$$的测量概率。
• 物理模型：在执行测量$$的状态$$下测量0的概率$$由$$给定
• 观测数据：状态$$的操作参数化：表示一组固定的随机二元射影测量值$$（一个量子位$$，两个量子位$$）
• 问题：对于固定的一组随机二元射影测量$$，测量$$的Operational参数化（一个量子位$$，两个量子位$$）

实验结果如下：

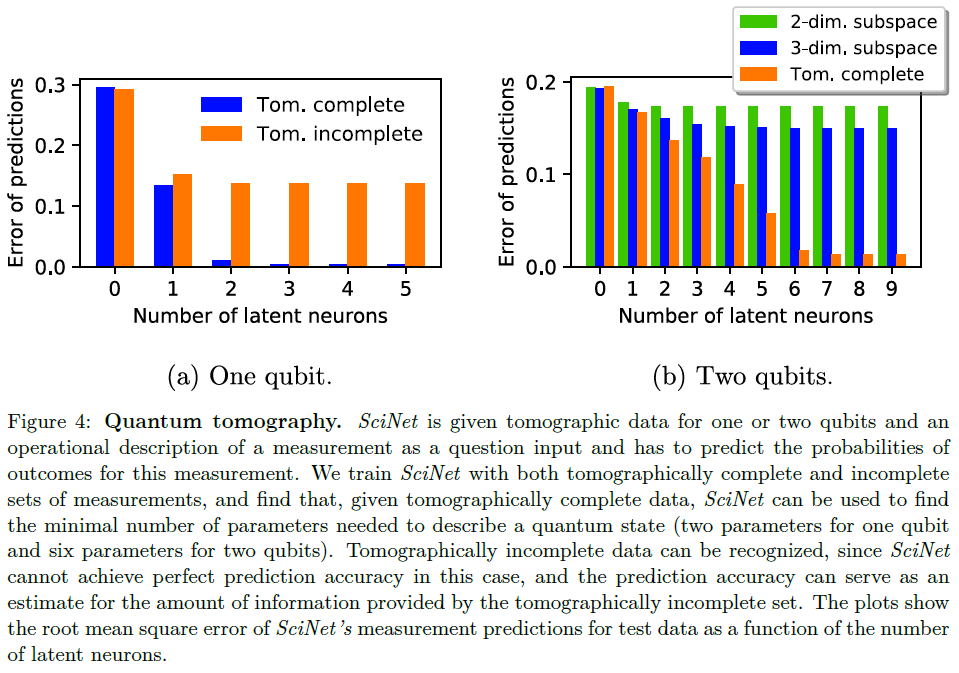
通过实验发现，SciNet可以在不提供先验物理知识的条件下确定表述状态$$最小的参数数量。同时，SciNet还能分辨tomographically complete和tomographically incomplete。

Heliocentric Model of the Solar System

日心说模型：

• 问题：在给定初始条件下预测相对与地球的太阳和火星的角度$$和$$
• 物理模型：地球和火星围绕太阳以一定角速度做近似圆周运动
• 观测数据：给定初始角度，随机选择周周期的哥白尼的观测数据

模型的实现稍有变化，如下图所示：

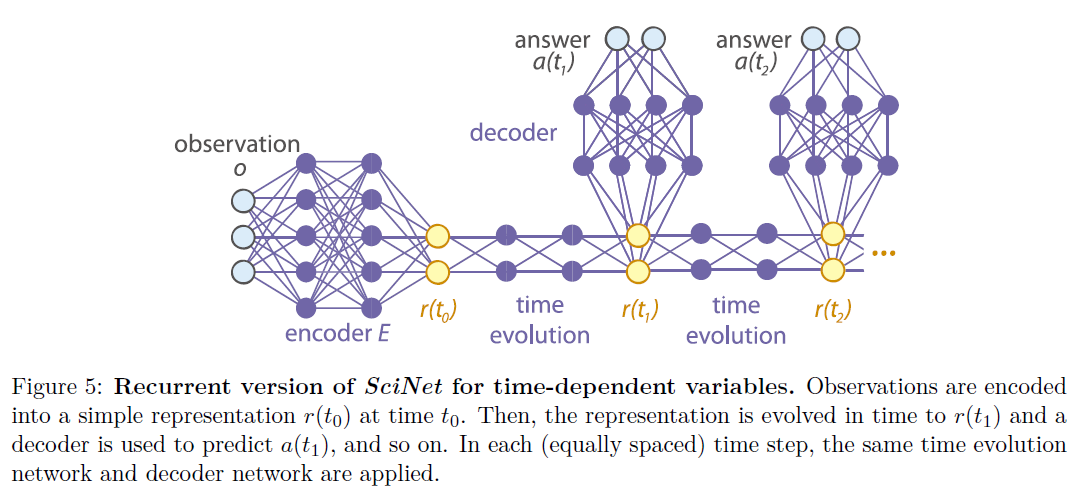
这样，对于不同时间都对应一个隐变量$$，而且隐变量是时间依赖的，对于一个隐变量$$有一个解码器来输出答案。

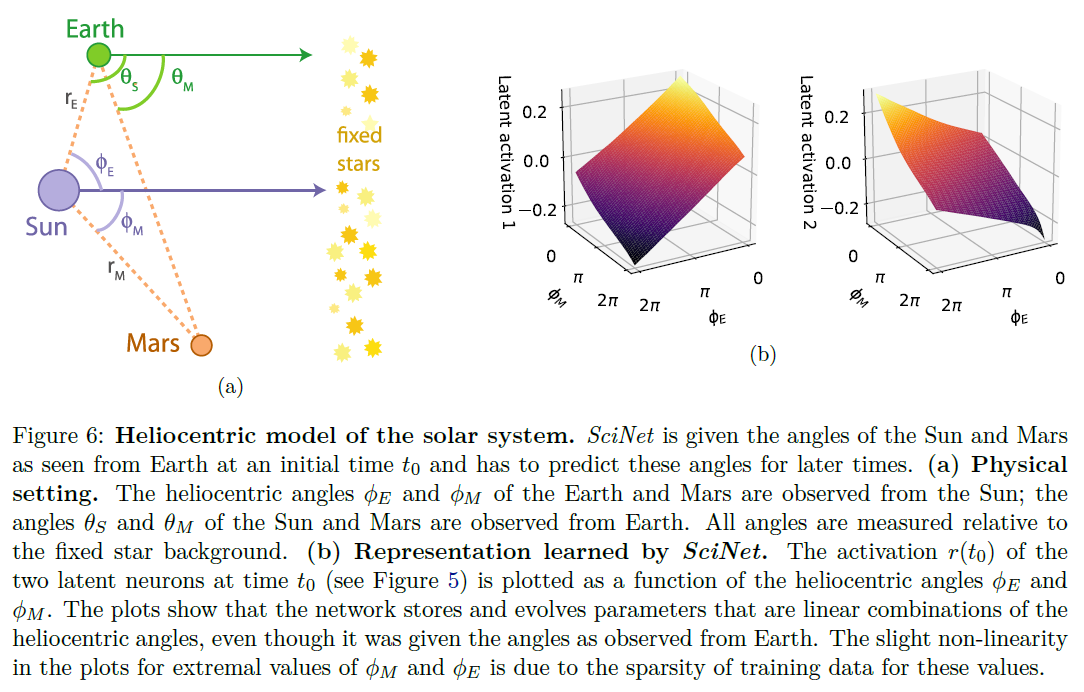
实验结果表示，SciNet不仅正确预测了太阳和火星相对地球的角度，同时隐变量揭示了火星和地球相对太阳的角度。