Transfer Anomaly Detection by Inferring Latent Domain Representations

Introduction

作者提出了一种利用迁移学习提升target domain异常检测性能的算法。文中指出现有的基于迁移学习的异常检测算法需要对每个 target domain 进行单独训练，这样做会带来很大的计算开销。本文通过latent domain vectors来实现无需重新训练的异常检测。latent domain vectors是domain的一种隐含表示，通过该domain中的正常样本得到。在本文中，anomaly score function通过Auto-encoder得到。

Proposed Method

Task

令\(\mathbf{X}_d^+:=\{\mathbf{x}^+_{dn}\}^{N^+_d}_{n=1}\)为第\(d\)个domain的异常样本集，\(\mathbf{x}_{dn}^+\in\mathbb{R}^M\)为其中第\(n\)个样本的\(M\)维特征向量，\(N^+_d\)为第\(d\)个domain异常样本的数量。

类似的，令\(\mathbf{X}_d^-:=\{\mathbf{x}^-_{dn}\}^{N^-_d}_{n=1}\)为第\(d\)个domain的正常样本集。我们假设对于每个domain都有\(N^+_d\ll N^-_d\)，且特征向量维度都为\(M\)。

假设在 source domain \(D_S\)都有正常样本和异常样本，记为\(\{\mathbf{X}^+_d\cup\mathbf{X}_d^-\}^{D_S}_{d=1}\)，在 target domain \(D_T\)只有正常样本\(\{\mathbf{X}_d^-\}^{D_S+D_T}_{d=D_S+1}\)。我们的目标是得到一个对于 target domain 合适的 domain-specific 的异常打分函数。

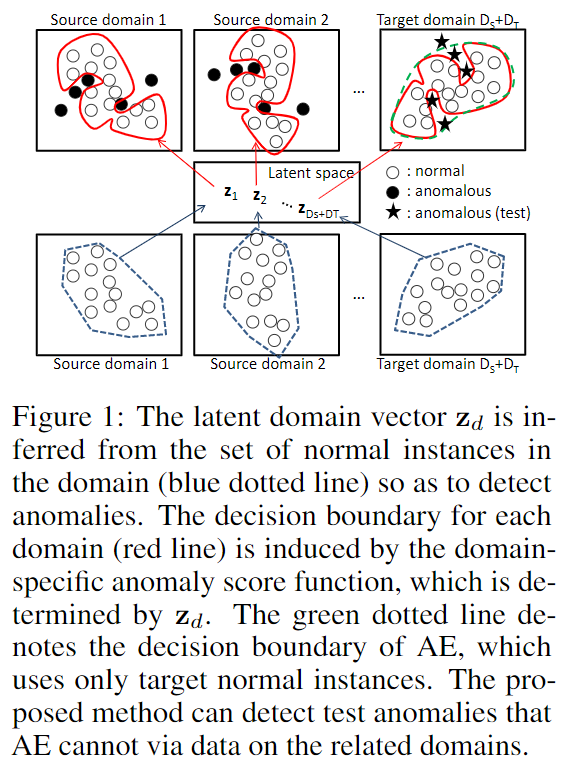
Domain-specific Anomaly Score Function

我们基于Auto-encoder定义异常打分函数。对于每个domain，我们假设存在一个\(K\)维的隐变量\(\mathbf{z}_d\in\mathbb{R}^K\)。对于第\(d\)个 domain，异常打分函数定义如下： \[ s_\theta(\mathbf{x}_{dn}|\mathbf{z}_d):=\parallel\mathbf{x}_{dn}-G_{\theta_G}(F_{\theta_F}(\mathbf{x}_{dn},\mathbf{z}_d))\parallel^2 \] 其中参数\(\theta:=(\theta_G,\theta_F)\)在所有 domain 之间共享。

Models for Latent Domain Vectors

隐变量\(\mathbf{z}_d\)是无法观测到的，只能通过数据来估计。首先\(\mathbf{z}_d\)在\(\mathbf{X}_d^-\)条件下的条件分布假设为高斯分布：

\[ q_\theta(\mathbf{z}_d|\mathbf{X}_d^-):=\mathcal{N}(\mathbf{z}_d|\mu_\phi(\mathbf{X}_d^-),\text{diag}(\sigma_\phi^2(\mathbf{X}_d^-))) \] 其中均值\(\mu_\phi(\mathbf{X}_d^-)\in\mathbb{R}^K\)和方差\(\sigma^2_\phi(\mathbf{X}_d^-)\in\mathbb{R}^K_+\)由神经网络建模，且在所有 domain 之间共享。在\(\mathbf{X}_d^-\)给定的时候，我们便能够推断出该 domain 对应的隐变量，

\(q_\phi\)的输入为正常样本的集合，故神经网络需要满足permutation invariant。\(\tau(\mathbf{X}_d^-)=\rho(\sum_{n=1}^{N_d^-}\eta(\mathbf{x}_{dn}^-))\)，其中\(\tau(\mathbf{X}_d^-)\)表示\(\mu_\phi(\mathbf{X_d^-})\)或\(\ln\sigma_\phi^2(\mathbf{X}_d^-)\)，\(\rho\)和\(\eta\)为神经网络，

Objective Function

目标函数由anomaly score函数和隐变量组成。第\(d\)个domain在对应的隐变量\(\mathbf{z}_d\)条件下的目标函数为：

\[ L_d(\theta|\mathbf{z}_d):=\frac{1}{N_d^-}\sum\limits_{n=1}^{N_d^-}s_\theta(\mathbf{x}_{dn}^-|\mathbf{z}_d)-\frac{\lambda}{N_d^-N_d^+}\sum\limits_{n,m=1}^{N_d^-,N_d^+}f(s_\theta(\mathbf{x}_{dm}^+|\mathbf{z}_d)-s_\theta(\mathbf{x}_{dn}^-|\mathbf{z}_d)) \]

其中\(\lambda\geq 0\)为超参数，\(f\)为sigmoid函数。公式的第一项表示第\(d\)个domain正常样本对应的anomaly score。第二项为可微分的AUC。异常样本的anomaly score应当大于正常样本，所以对任何\(\mathbf x_{dm}^+\in\mathbf X_d^+, \mathbf x_{dn}^-\in\mathbf X_d^-\)有\(s_\theta(\mathbf x_{dm}^+|\mathbf z_d)>s_\theta(\mathbf x_{dn}^-|\mathbf z_d)\)。第二项\(\frac{\lambda}{N_d^-N_d^+}\sum\limits_{n,m=1}^{N_d^-,N_d^+}f(s_\theta(\mathbf{x}_{dm}^+|\mathbf{z}_d)-s_\theta(\mathbf{x}_{dn}^-|\mathbf{z}_d))\)的取值范围是\([0,1]\)，当所有的\(s_\theta(\mathbf{x}_{dm}^+|\mathbf{z}_d)\gg s_\theta(\mathbf{x}_{dm}^-|\mathbf{z}_d)\)时该项为1，当所有的\(s_\theta(\mathbf{x}_{dm}^+|\mathbf{z}_d)\ll s_\theta(\mathbf{x}_{dm}^-|\mathbf{z}_d)\)时该项为0，所以最小化该项的相反数相当于鼓励\(s_\theta(\mathbf{x}_{dm}^+|\mathbf{z}_d)\gg s_\theta(\mathbf{x}_{dm}^-|\mathbf{z}_d)\)。

因为隐变量\(\mathbf z_d\)包含不确定性，我们应该在目标函数里考虑这一点： \[ \mathcal{L}_d(\theta,\phi):=\mathbb{E}_{q_\phi(\mathbf{z}_d|\mathbf{X}_d^-)}\left[L_d(\theta|\mathbf{z}_d)\right]+\beta D_\text{KL}(q_\phi(\mathbf{z}_d|\mathbf{X}_d^-)\parallel p(\mathbf{z_d})) \]

第一项是\(L_d(\theta|\mathbf z_d)\)关于\(q_\phi(\mathbf z_d|\mathbf X_d^-)\)的期望，第二项是\(q_\phi(\mathbf z_d|\mathbf X_d^-)\)和\(p(\mathbf z_d):=\mathcal{N}(\boldsymbol 0,\boldsymbol I)\)的KL散度。第一项可以用monte carlo估计\(\mathbb{E}_{q_\phi(\mathbf{z}_d|\mathbf{X}_d^-)}\left[L_d(\theta|\mathbf{z}_d)\right]\approx\frac{1}{L}\sum_{\ell=1}^L L_d(\theta|\mathbf z_d^{(\ell)})\)，除此之外还需要用到reparametrization trick。

对于第\(d\)个target domain，因为没有异常样本（假设），所以\(L_d(\theta|\mathbf{z}_d):=\frac{1}{N_d^-}\sum\limits_{n=1}^{N_d^-}s_\theta(\mathbf{x}_{dn}^-|\mathbf{z}_d)\)，有： \[ \mathcal{L}_d(\theta,\phi):=\mathbb{E}_{q_\phi(\mathbf{z}_d|\mathbf{X}_d^-)}\left[\frac{1}{N_d^-}\sum\limits_{n=1}^{N_d^-}s_\theta(\mathbf{x}_{dn}^-|\mathbf{z}_d)\right]+\beta D_\text{KL}(q_\phi(\mathbf{z}_d|\mathbf{X}_d^-)\parallel p(\mathbf{z}_d)) \]

所以总的损失函数为各domain对应的损失函数之和\(\mathcal{L}(\theta,\phi):=\sum_{d=1}^{D_S+D_T}\alpha_d\mathcal{L}_d(\theta,\phi)\)。

Inference

训练好之后，domain-specific的anomaly score可以由下式计算出：

\[ s(\mathbf{x}_{d^\prime}):=\int s_{\theta_*}(\mathbf{x_{d^\prime}}|\mathbf{z}_{d^\prime})q_{\phi_*}(\mathbf{z}_{d^\prime}|\mathbf{X}_{d^\prime}^-)\mathrm{d}\mathbf{z}_{d^\prime}\approx\frac{1}{L}\sum\limits_{\ell=1}^L s_{\theta_*}(\mathbf{x}_{d^\prime}|\mathbf{z}_{d^\prime}^{(\ell)}) \]

Experiments

Data

实验包含五个数据集，第一个是合成数据集。如下图(a)所示，围绕\((0,0)\)有\(8\)个圈，每个圈包含了一个内圈作为异常样本，第\(7\)个圈被选为target domain，其余的为source domain。第二个是MNIST-r，是加入旋转的MNIST，包含6个domain，其中数字“4”被选为异常样本，其余为正常。第三个为Anuran Calls，包含5个domain。第四个是Landmine，主要用在多任务学习中。第五个是IoT，网络流量数据，包含8个domain。

Comparison Methods

对比的baseline包括NN（普通多层神经网络），NNAUC（加入可微分AUC作为损失函数），AE（普通Autoencoer），AEAUC（加入可微分AUC的AE），OSVM（单类支持向量机），CCSA，TOSVM和OTL。

Results

4个真实数据集的结果如下：

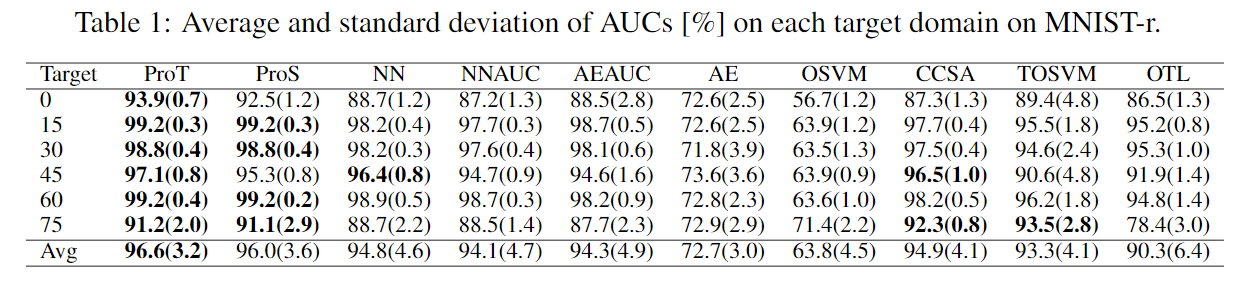
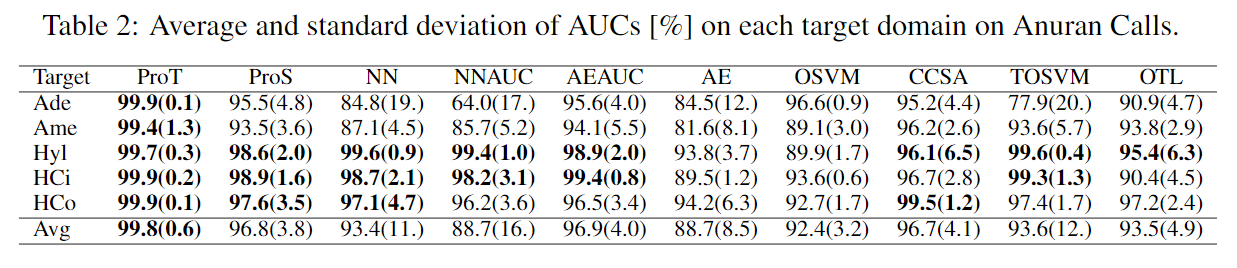
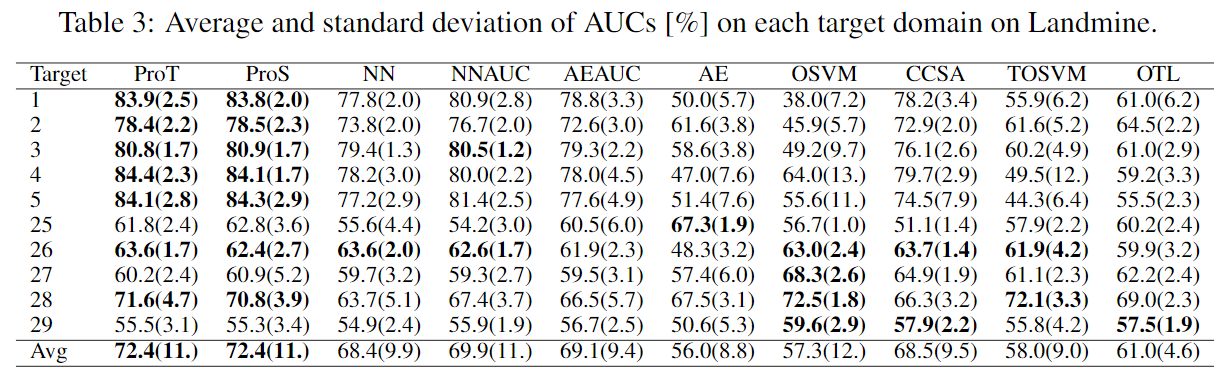
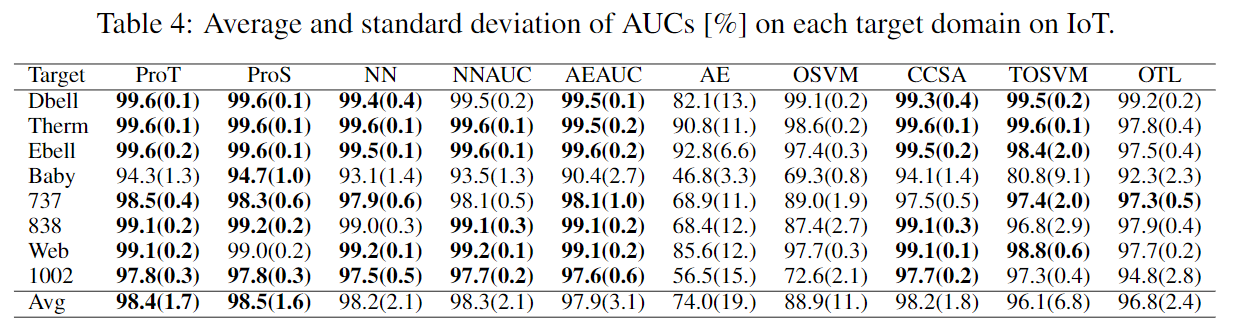
表5为考虑隐变量不确定性的ablation study。将原来的公式\(\mathcal{L}_d(\theta,\phi):=\mathbb{E}_{q_\phi(\mathbf{z}_d|\mathbf{X}_d^-)}\left[L_d(\theta|\mathbf{z}_d)\right]+\beta D_\text{KL}(q_\phi(\mathbf{z}_d|\mathbf{X}_d^-)\parallel p(\mathbf{z_d}))\)中\(q_\phi(\mathbf z_d|\mathbf X_d^-)\)用迪利克雷分布\(q_\phi(\mathbf z_d|\mathbf X_d^-)=\delta(\mathbf z_d-\mu_\phi(\mathbf X_d^-))\)代替并且去掉KL散度。

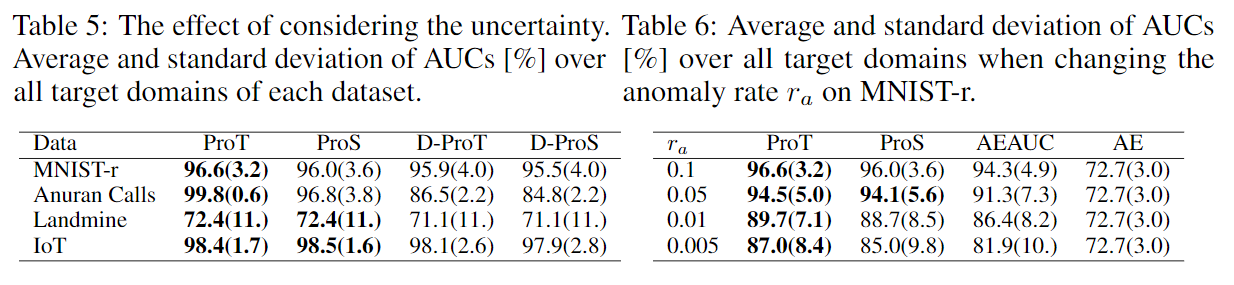
表6展示了不同异常比例对效果的影响。