Deep Anomaly Detection with Deviation Networks
本文最后更新于:2 年前
Introduction
本文关注Deep Anomaly Detection,也就是用深度学习的方法来进行异常检测。文中提到现有的Deep Anomaly Detection存在两个弊端:一个是采用深度学习方法来进行特征学习,然后通过下游任务得到Anomaly Score,相比文中End-to-End的Anomaly Score学习,存在优化不充分的风险;另一个是现有的方法主要是无监督学习,无法利用已知的信息(如少量标签)。为此,本文提出了一种端到端的异常检测框架,来解决上述问题。
本文的主要贡献如下:
- 提出了一种端到端的异常检测框架,直接学习
Anomaly Score并且可以利用已知信息; - 基于提出的框架,文中提出了一种实例方法 (DevNet)。
Proposed Model
End-To-End Anomaly Score Learning
Problem Statement
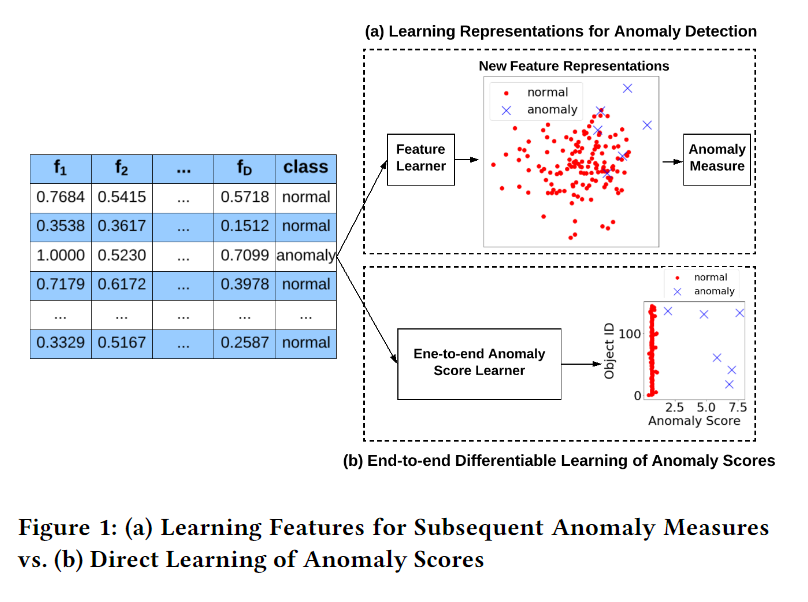
为了区别于传统的两阶段异常检测(先学习特征表示,然后在学到的特征上定义一个anomaly measure来得到anomaly score),作者对端到端的异常检测问题重新进行形式化。
给定\(N+K\)个样本\(\mathcal{X}=\{\boldsymbol x_1,\boldsymbol x_2,\cdots,\boldsymbol x_N,\boldsymbol x_{N+1},\cdots,\boldsymbol x_{N+K}\}\),其中\(\boldsymbol x_i\in\mathbb{R}^D\),无标签样本集\(\mathcal{U}=\{\boldsymbol x_1,\boldsymbol x_2,\cdots,\boldsymbol x_N\}\),有标签样本集\(\mathcal{K}=\{\boldsymbol x_{N+1},\cdots,\boldsymbol x_{N+K}\}\),且\(K\ll N\)。异常检测的目标是学习一个anomaly scoring function\(\phi:\mathcal{X}\mapsto\mathbb{R}\)使得\(\phi(\boldsymbol x_i)>\phi(\boldsymbol x_j)\),其中\(\boldsymbol x_i\)为异常样本,\(\boldsymbol x_j\)为正常样本。
The Proposed Framework
为了解决这个问题,文中提出了一种通用异常检测框架,模型框架如下图所示:
模型框架如下图所示:
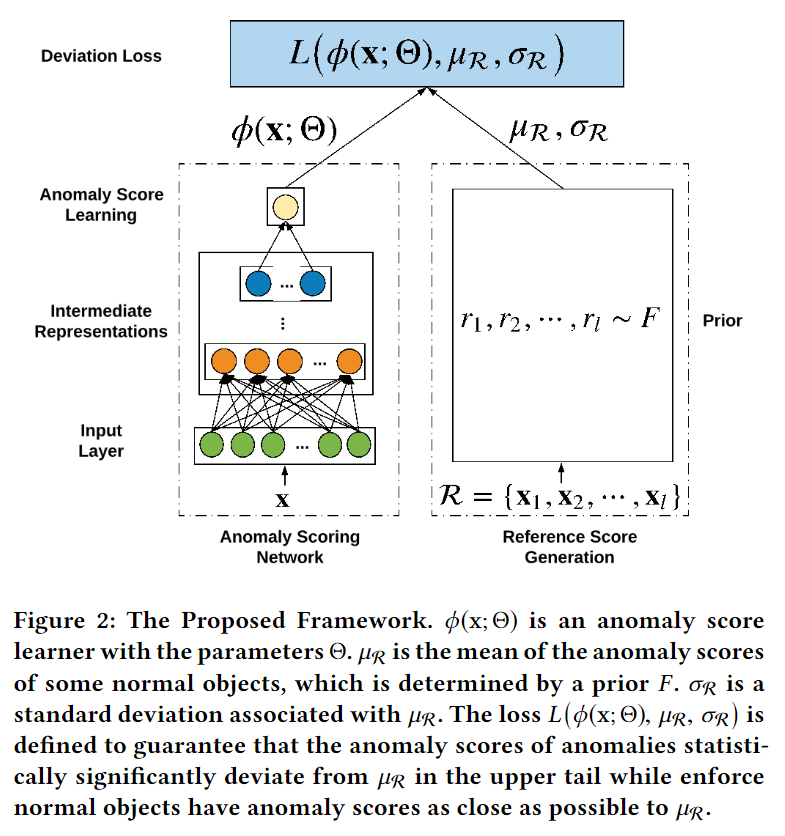
主要包含三个部分:
- anomaly scoring network. 图中左边的部分,一个函数\(\phi\),输入样本\(\mathbf{x}\),输出
anomaly score - reference score generator. 图中右边的部分。只有一个anomaly scoring network并不能进行训练,需要训练的目标。为此加入reference score generator,输入为随机选择的\(l\)个正常样本,输出
reference score(这\(l\)个正常样本anomaly score的均值,记为\(\mu_\mathcal{R}\)) - deviation loss. \(\phi(\mathbf{x})\),\(\mu_\mathcal{R}\)及对应的标准差\(\sigma_\mathcal{R}\)作为
deviation loss函数的输入。因为\(\mu_\mathcal{R}\)和\(\sigma_\mathcal{R}\)对应正常样本集的均值和方差,那么异常样本的anomaly score应该和\(\mu_\mathcal{R}\)差别比较大,而正常样本则应该接近\(\mu_\mathcal{R}\)。
Deviation Networks
下面是上述三个部件的具体实现。
End-To-End Anomaly Scoring Network
记\(\mathcal{Q}\in\mathbb{R}^M\)为中间表示空间,anomaly scoring network\(\phi(\cdot;\Theta):\mathcal{X}\mapsto\mathbb{R}\)可以定义为数据表示学习\(\psi(\cdot;\Theta_t):\mathcal{X}\mapsto\mathcal{Q}\)和异常分数学习\(\eta(\cdot;\Theta_s):\mathcal{Q}\mapsto\mathbb{R}\)两阶段的组合,其中\(\Theta=\{\Theta_t,\Theta_s\}\)。
\(\psi(\cdot;\Theta_t)\)可以用一个\(H\)层神经网络来实现: \[ \mathrm{q}=\psi(\mathbf{x};\Theta_t) \] 其中\(\mathbf{x}\in\mathcal{X}\),\(\mathrm{q}\in\mathcal{Q}\)。
\(\eta(\cdot;\Theta_s)\)可以用一个单层的神经网络来实现: \[ \eta(\mathrm q;\Theta_s)=\sum\limits_{i=1}^M w_i^oq_i+w_{M+1}^o \] 其中\(\mathrm q\in\mathcal Q\),\(\Theta_s=\{\mathbf{w}^o\}\)。
所以有: \[ \phi(\mathbf{x};\Theta)=\eta(\psi(\mathbf{x};\Theta_t);\Theta_s) \]
Gaussian Prior-based Reference Scores
有两种方法来获得\(\mu_\mathcal{R}\),一种是data-driven,一种是prior-driven。如果是data-driven的话则采用另一个神经网络,文中表示为了更好的解释性和计算效率,所以采用的是prior-driven。 \[ \begin{align} r_1,r_2,\cdots,r_l\sim \mathcal{N}(\mu,\sigma^2),\\ \mu_\mathcal{R}=\frac{1}{l}\sum\limits_{i=1}^l r_i \end{align} \] 在文中,采用的prior是标准高斯分布。
Z-Score Based Deviation Loss
anomaly scoring network的优化目标可以定义为Z-Score的方式: \[
dev(\boldsymbol x)=\frac{\phi(\boldsymbol x;\Theta)-\mu_{\mathcal{R}}}{\sigma_{\mathcal{R}}}
\] \(dev(\boldsymbol x)\)可以看作是样本偏离标准的程度,而我们肯定希望异常样本偏离标准越大,正常样本越接近标准。文中采用的损失函数是Contrastive Loss: \[
L(\phi(\boldsymbol x;\Theta),\mu_\mathcal{R},\sigma_\mathcal{R})=(1-y)|dev(\boldsymbol x)| + y \max(0, a - dev(\boldsymbol x))
\] Contrastive Loss的直观解释可以看下图:
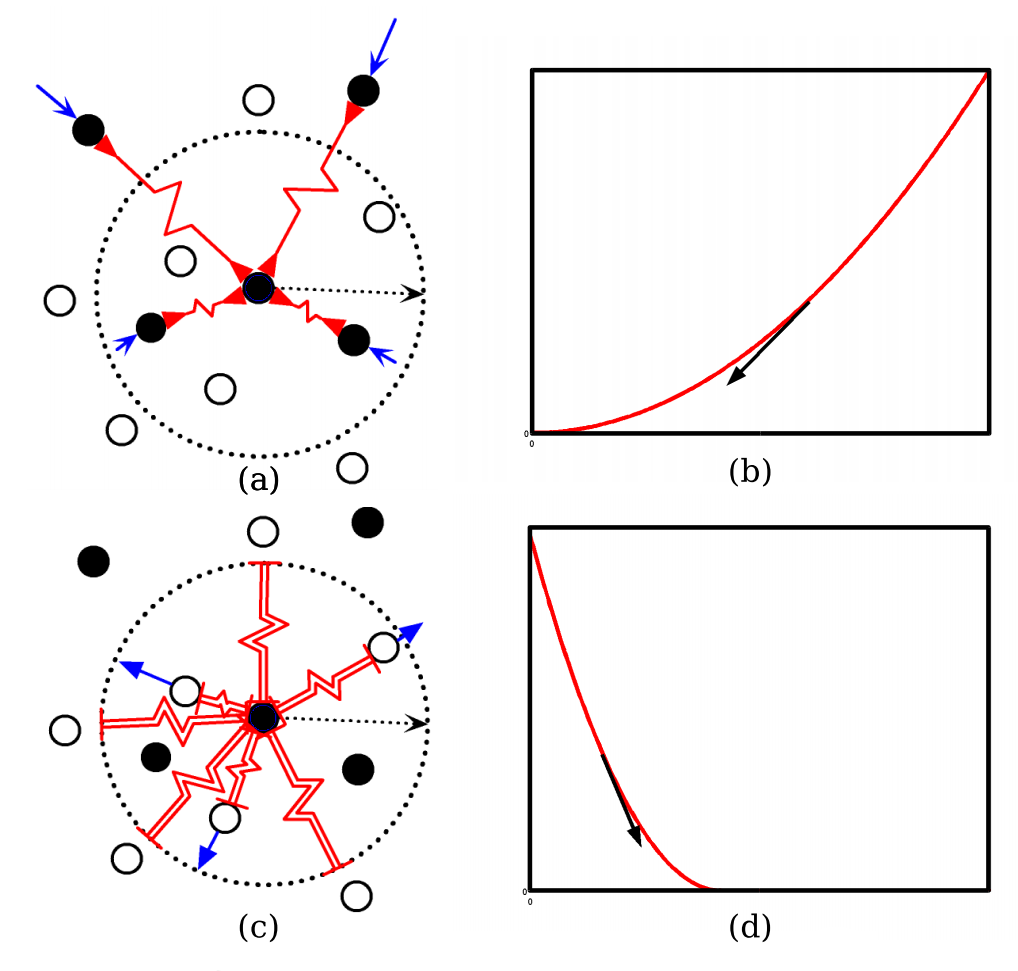
对于负例(正常),优化过程将他们尽量向原点靠近,对于正例(异常),优化过程将他们拉向边界。
The DevNet Algorithm
DevNet的算法流程图如下:
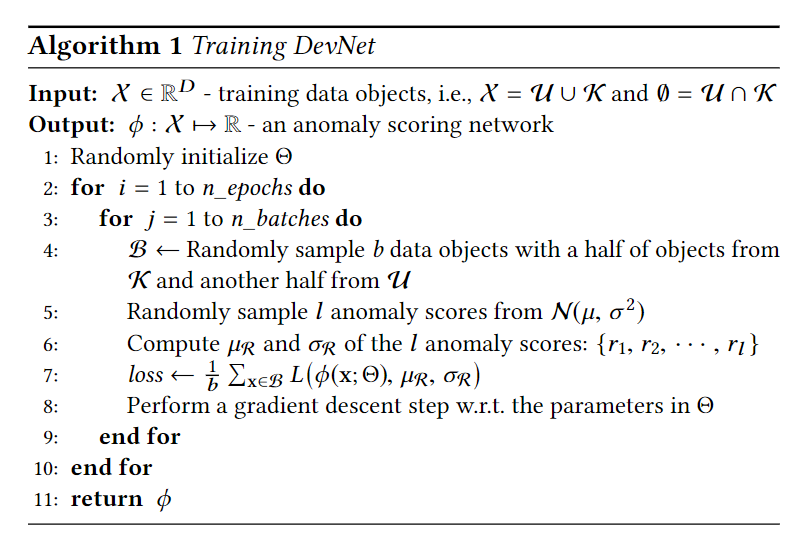
Interpretability of Anomaly Scores
因为reference score generator选择的是确定的高斯分布,于是可以用概率论给出一些解释性。作者给出了一个结论,
PROPOSITION: 设\(\boldsymbol x\in\mathcal{X}\),\(z_p\)为\(\mathcal{N}(\mu,\sigma^2)\)的分位数,那么\(\phi(\boldsymbol x)\)在区间\(\mu\pm z_p\sigma\)的概率为\(2(1-p)\)。
例如,假设\(p=0.95\),那么\(z_{0.95}=1.96\),表示异常分数高于1.96的样本将以0.95的置信度为异常。
Experiment
实验用到了9个数据集,4个Baseline (REPEN,DSVDD,FSNET,iForest),以及ROC和PR曲线两种评测标准。
Effectiveness in Real-world Data Sets
Experiment Settings
这一个实验主要是为了验证算法在真实场景下的效果,即大量无标签数据和极少量标签数据。训练集包含两部分,一部分是无标签数据\(\mathcal{U}\),包含\(2\%\)的异常样本,另一部分是有标签数据\(\mathcal{K}\),由随机采样\(0.005\%-1\%\)的训练数据和\(0.08\%-6\%\)的异常样本组成。
Findings
实验结果如下表所示:
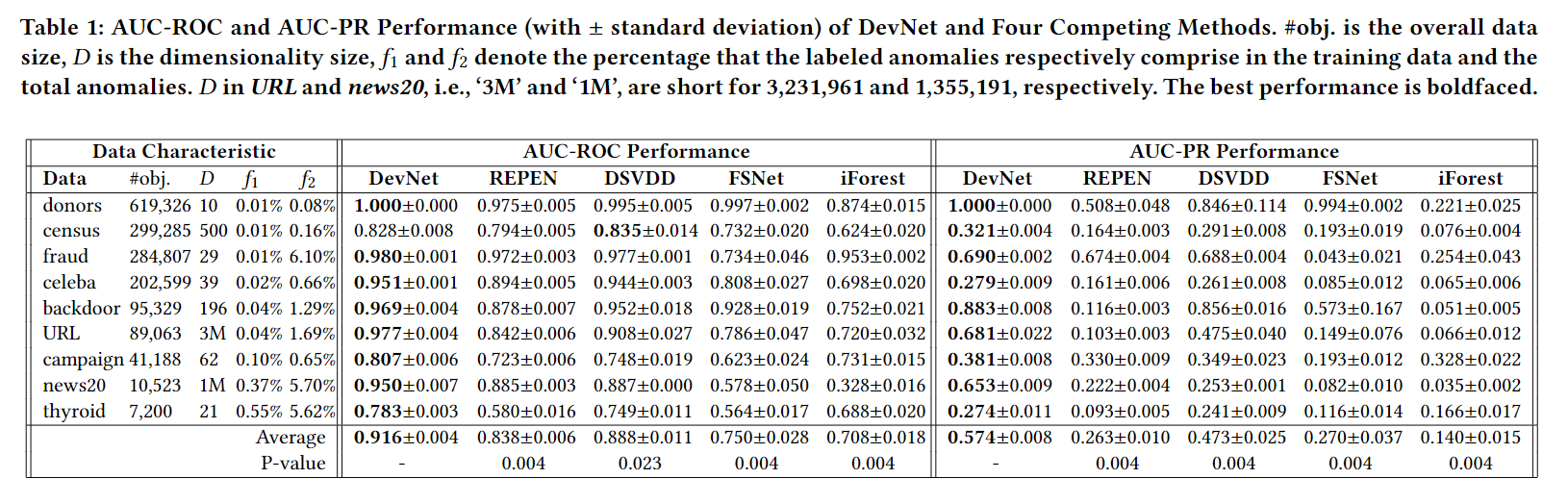
从结果上看来,本文提出的方法在所有数据集上都比Baseline好,说明DevNet端到端直接优化Anomaly Score的方式是有效的。
Data Efficiency
Experiment Settings
这一个实验主要是为了探究基于深度的异常检测方法的data efficiency。和上一个实验一样,无标签数据集包含\(2\%\)的异常,而有标签的异常数量从\(5\)到\(120\)不等。本实验试图回答以下两个问题:
DevNet的data efficiency如何?- 基于深度的方法在多大程度上能够利用标签信息?
Findings
在几个基于深度的Baseline中,DevNet的效果是最好的,同时在有标签异常非常有限的情况下,DevNet也能很好的利用标签信息,达到更好的效果。
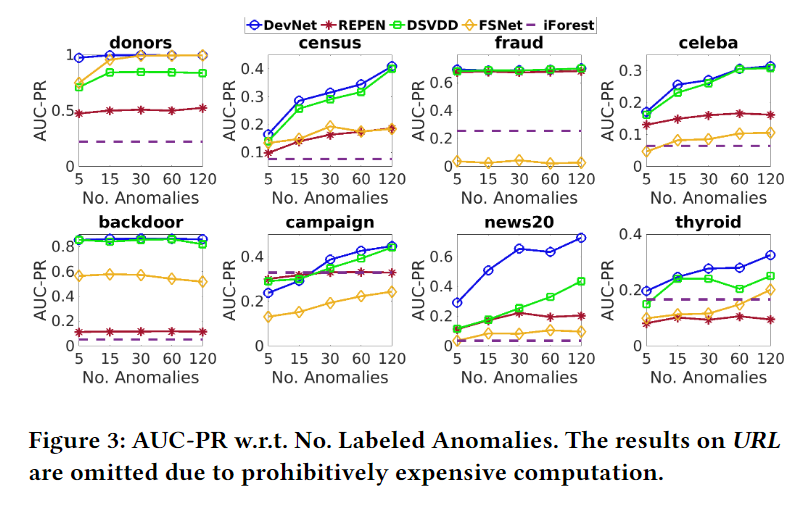
Robustness w.r.t. Anomaly Contamination
Experiment Settings
在第一个实验中,无标签数据集\(\mathcal{U}\)包含的是固定的异常比例\(2\%\),而在这个实验中,作者测试了从\(0\%\)到\(20\%\)之间不同异常比例来测试算法的鲁棒性(即使\(\mathcal{U}\)中包含异常,由于没有标签,在训练的时候仍然假设都为正常来进行训练)。本实验试图回答以下问题:
- 基于深度的异常检测方法的鲁棒性如何?
- 当训练集中异常污染的比例较高的时候基于深度的方法能否打败无监督的方法?
Findings
下图为实验结果:
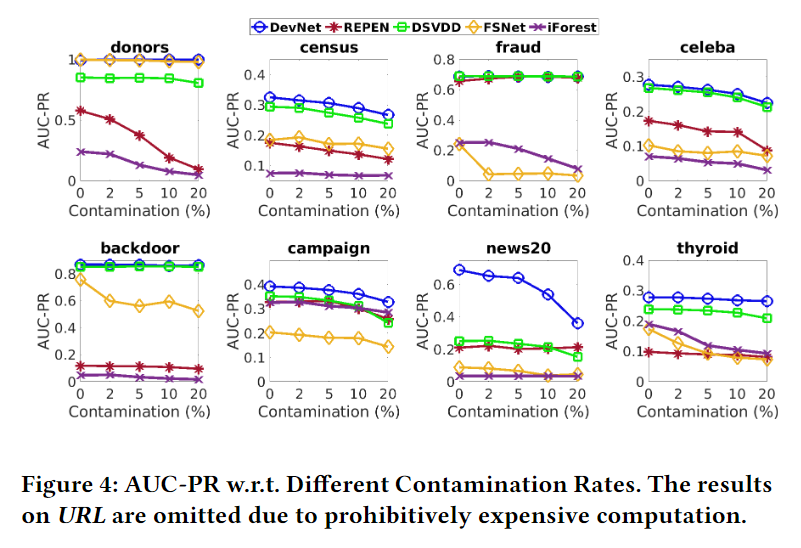
从结果上来看,DevNet比其他基于深度的方法鲁棒性更好,同时在高异常污染的情况下仍然比纯无监督方法效果要好。
Ablation Study
本实验设置了DevNet的三个变体(默认的DevNet-Def为单层隐层加上一个输出层)来进行消融实验,分别是:
DevNet-Rep,去掉了anomaly scoring network网络的输出层,对应end-to-end learning of anomaly scores和deviation loss;DevNet-Linear,去掉了网络中的非线性层,对应learning of non-linear features;DevNet-3HL,隐层数量为3层。
对比结果如下:
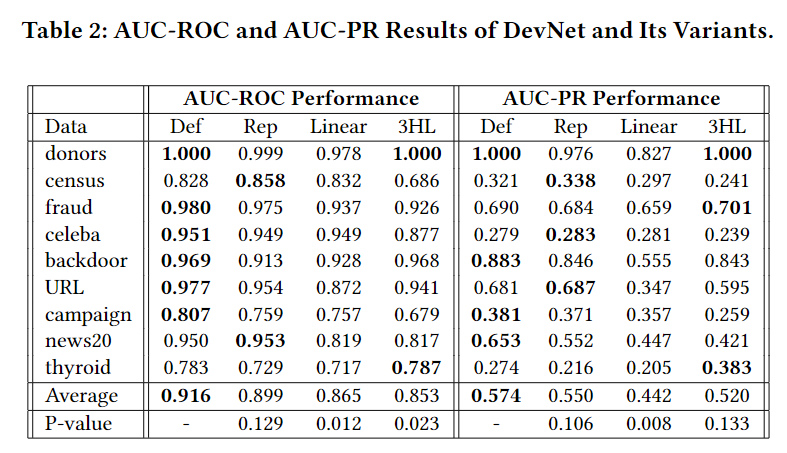
通过实验可以发现,DevNet-Rep说明了end-to-end learning of anomaly scores和deviation loss的有效性,而DevNet-Linear说明了learning of non-linear features的重要性。DevNet-3HL说明了加深网络并不总能带来性能的提升。
Scalability Test
这一个实验使用合成的数据来测试算法对大规模数据的处理能力,分别从Data Size和Data Dimensionality两方面来测试。结果如下:
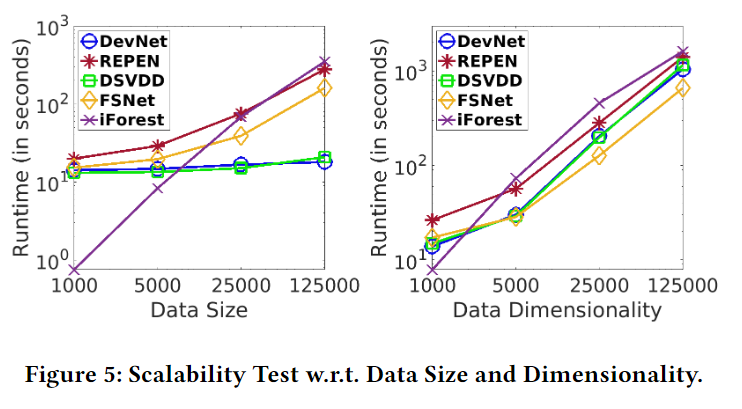
可以看出,DevNet对Data Size并不敏感,同时,面对高维数据,DevNet也没有表现出劣势。
本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!