Complementary Set Variational Autoencoder for Supervised Anomaly Detection
本文最后更新于:2 年前
Introduction
对于异常检测问题,异常的模式是多种多样的。有监督模型能够较好地处理训练集中出现过的模式,无监督模型能够处理训练集中未出现过的模式,但对于训练集中出现过的异常模型并没有学习。本文提出了一种既能学习训练集中出现过的异常模式,同时能处理未出现过的异常模式的方法。
Proposed Model
Conventional VAE
首先回顾一下原始的VAE。
原始VAE中的损失函数为: \[ \mathcal{L}(\boldsymbol{\theta},\boldsymbol{\phi};\boldsymbol{x})=\mathbb{E}_{q(\boldsymbol{z}|\boldsymbol{x};\boldsymbol{\phi})}[\log p(\boldsymbol{x}|\boldsymbol{z};\boldsymbol{\theta})]-\text{KL}[q(\boldsymbol{z}|\boldsymbol{x};\boldsymbol{\phi}\parallel p(\boldsymbol{z}))] \] 原文中作者证明了\(\mathcal{L}(\boldsymbol{\theta},\boldsymbol{\phi};\boldsymbol{x})\leq\log p(\boldsymbol{x};\boldsymbol{\theta})\),所以\(\mathcal{L}(\boldsymbol{\theta},\boldsymbol{\phi};\boldsymbol{x})\)可以看作是数据分布\(p(\boldsymbol{x})\)对数似然的一个下界。\(\mathcal{L}(\boldsymbol{\theta},\boldsymbol{\phi};\boldsymbol{x})\)又被称为证据下界 (ELBO)。\(\mathbb{E}_{q(\boldsymbol{z}|\boldsymbol{x};\boldsymbol{\phi})}[\log p(\boldsymbol{x}|\boldsymbol{z};\boldsymbol{\theta})]\)中的期望一般用蒙特卡洛来进行估计: \[ \begin{align} \mathcal{L}(\boldsymbol{\theta},\boldsymbol{\phi};\boldsymbol{x})\simeq& \frac{1}{L}\sum\limits_l\log p(\boldsymbol{x}|\boldsymbol{z}^{(l)};\boldsymbol{\theta})-\text{KL}[q(\boldsymbol{z}|\boldsymbol{x};\boldsymbol{\phi})\parallel p(\boldsymbol{z})],\\ \boldsymbol{z}^{(l)}&\sim q(\boldsymbol{z}|\boldsymbol{x};\boldsymbol{\phi}), \space l\in\{1,2,\cdots,L\} \end{align} \] 对于隐变量\(\boldsymbol{z}\),一般假设先验服从标准高斯分布,后验服从均值为\(\mu\),方差为\(\sigma^2\)的高斯分布,故KL散度能直接写出解析式: \[ \mathcal{L}(\boldsymbol{\theta},\boldsymbol{\phi};\boldsymbol{x})\simeq \frac{1}{L}\sum\limits_l\log p(\boldsymbol{x}|\boldsymbol{z}^{(l)};\boldsymbol{\theta})-C(-\frac{1}{2}-\log\sigma+\frac{1}{2}\sigma^2+\frac{1}{2}\mu^2) \] 使用VAE来做异常检测通常是在正常数据上进行训练,在检测阶段,如果是异常样本,那么VAE不能很好地重构它,这样会导致较大的重构误差。
Prior Distribution for Anomalies
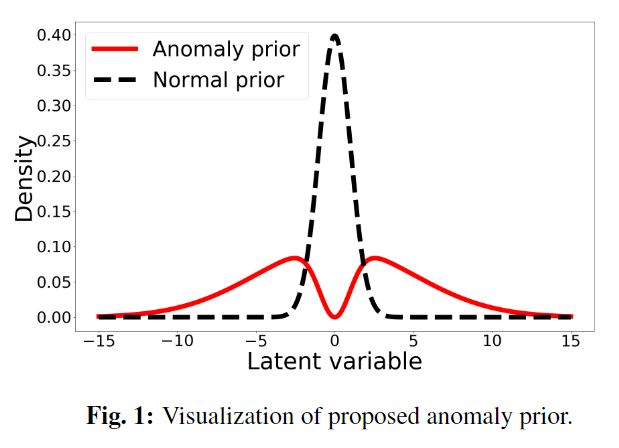
在原始VAE异常检测中,无论输入样本\(\boldsymbol{x}\)是否异常,VAE都会使对应编码的后验\(p(\boldsymbol{z}|\boldsymbol{x})\)服从高斯分布,且施加标准高斯分布的约束。在本文中,作者对异常和正常样本对应的隐变量的先验分布做了不同假设。首先,正常先验依然是标准高斯分布,记为\(p_n(\boldsymbol{z})\)。而对于异常先验,作者认为异常即为“不正常”,和正常是补集的关系。作者在文中定义异常先验分布\(p_a(\boldsymbol{z})\)为: \[ p_a(\boldsymbol{z})=\frac{1}{Y^\prime}(\max\limits_{\boldsymbol{z}^\prime}p_n(\boldsymbol{z}^\prime)-p_n(\boldsymbol{z})) \]
其中\(Y^\prime\)为使\(p_a(\boldsymbol{z})\)成为一个概率分布的调节因子。实际上,\(Y^\prime\)往往会成为无限大,因为\(p(\boldsymbol z)\)在整个定义域上都有定义。为了解决这个问题,作者加入了\(p_w(\boldsymbol z)\),一个在每个维度都足够宽的辅助分布:
\[ p_a(\boldsymbol z)=\frac{1}{Y}p_w(\boldsymbol z)\left(\max\limits_{\boldsymbol z^\prime}p_n(\boldsymbol z^\prime)-p_n(\boldsymbol z)\right) \]
其中\(Y\)为有限的常数。在文中\(p_n(\boldsymbol z)\)和\(p_w(\boldsymbol z)\)都为高斯分布,那么\(p_a(\boldsymbol z)\)的具体形式为:
\[ p_a(\boldsymbol z)=\frac{1}{Y}\mathcal{N}(\boldsymbol z;\boldsymbol 0,\boldsymbol s^2)\{\max\limits_{\boldsymbol z^\prime}\mathcal N(\boldsymbol z^\prime;\boldsymbol 0,\boldsymbol 1)-\mathcal N(\boldsymbol z;\boldsymbol 0,\boldsymbol 1)\} \]
其中:
\[ \max\limits_{\boldsymbol z^\prime}\mathcal N(\boldsymbol z^\prime;\boldsymbol 0,\boldsymbol 1)=\frac{1}{\sqrt{2\pi}} \]
\[ Y=\int_{-\infty}^{\infty}p_a(\boldsymbol z)\mathrm{d}\boldsymbol z=\frac{1}{\sqrt{2\pi}}\left\{1-\frac{1}{\boldsymbol s^2+1}\right\} \]
\(\boldsymbol s^2\)为超参数,控制分布的宽度。用文中的先验替换VAE原始的KL散度,可写为:
\[ \text{KL}\left[q(\boldsymbol z|\boldsymbol x;\phi)\parallel p_a(\boldsymbol z)\right]=\int_{-\infty}^\infty\mathcal{N}(\boldsymbol z;\boldsymbol \mu,\boldsymbol \sigma^2)\log\frac{\mathcal N(\boldsymbol z;\boldsymbol\mu,\boldsymbol\sigma^2)}{\frac{1}{Y}\mathcal N(\boldsymbol z;\boldsymbol 0,\boldsymbol s^2)\left\{\frac{1}{2\pi}-\mathcal N(\boldsymbol z;\boldsymbol0,\boldsymbol 1)\right\}}\mathrm{d}\boldsymbol z \]
展开后:
\[ \begin{align} \text{KL}\left[q(\boldsymbol z|\boldsymbol x;\phi)\parallel p_a(\boldsymbol z)\right]&= \int_{-\infty}^\infty\mathcal{N}(\boldsymbol z;\boldsymbol \mu,\boldsymbol \sigma^2)\log\mathcal{N}(\boldsymbol z;\boldsymbol\mu,\boldsymbol\sigma^2)\mathrm{d}\boldsymbol z\\ &+\log Y\\ &-\int_{-\infty}^\infty\mathcal{N}(\boldsymbol z;\boldsymbol \mu,\boldsymbol \sigma^2)\log\mathcal{N}(\boldsymbol z;\boldsymbol 0,\boldsymbol s^2)\mathrm{d}\boldsymbol z\\ &-\int_{-\infty}^\infty\mathcal{N}(\boldsymbol z;\boldsymbol \mu,\boldsymbol \sigma^2)\log\left\{\frac{1}{\sqrt{2\pi}}-\mathcal{N}(\boldsymbol z;\boldsymbol 0, \boldsymbol 1)\right\}\mathrm{d}\boldsymbol z \end{align} \]
使用泰勒展开,\(\log (x+\frac{1}{2\pi})\simeq-\log 2\pi+2\pi x\),KL散度可以用下式估计:
\[ \begin{align} \text{KL}\left[q(\boldsymbol z|\boldsymbol x;\phi)\parallel p_a(\boldsymbol z)\right]&\simeq\sqrt{\frac{2\pi}{\boldsymbol\sigma^2+1}}\exp\left(\frac{-\boldsymbol\mu^2}{2(\boldsymbol\sigma^2+1)}\right)\\ &+\frac{\boldsymbol\mu^2+\boldsymbol\sigma^2}{2\boldsymbol s^2}-\log\boldsymbol\sigma+\log\boldsymbol s+\log\left(\sqrt{\boldsymbol s^2+1}-1\right)\\ &-\frac{\log(\boldsymbol s^2+1)}{2}+\frac{\log(2\pi)-1}{2} \end{align} \]
下图为一维时\(p_n(\boldsymbol z)\)和\(p_a(\boldsymbol z)\)的示例:
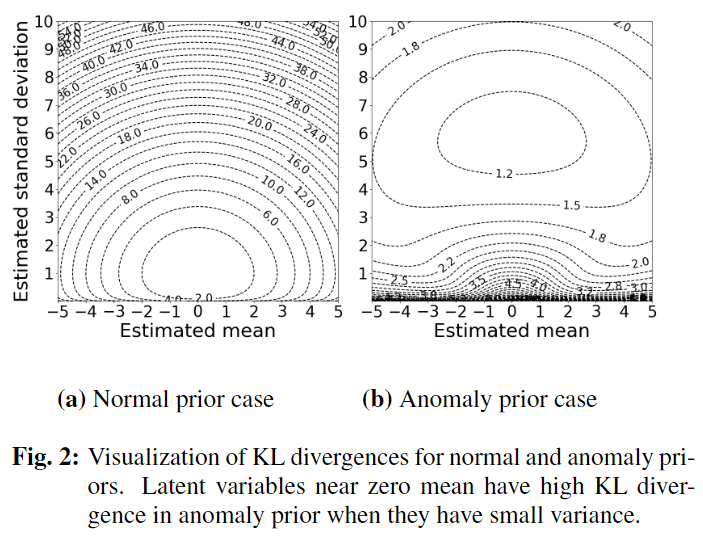
Implementation of proposed method
文中使用编码器输出的分布\(\mathcal{N}(\boldsymbol z;\boldsymbol \mu, \boldsymbol \sigma^2)\)与标准正态分布之间的KL散度来作为异常分数。在每一轮的训练过程中,加入一轮使用Anomaly Prior的训练。

Experiments
MNIST
作者设计了两个Task:
- Task 1. \(N\) vs. \(\bar{N}\). 将手写数字中的一个作为已知异常,其他作为正常,并加入均匀分布作为未知的异常。
- Task 2. 手写数字被分为3组:已知异常,正常,未知异常。
细节如下表所示:

在实现上,使用Adam优化器,batch_size为100,epochs为200。Encoder和Decoder都由三层感知机组成,超参数\(s^2\)设置为400。评测标准使用AUC (area under the receiver characteristic curve)。
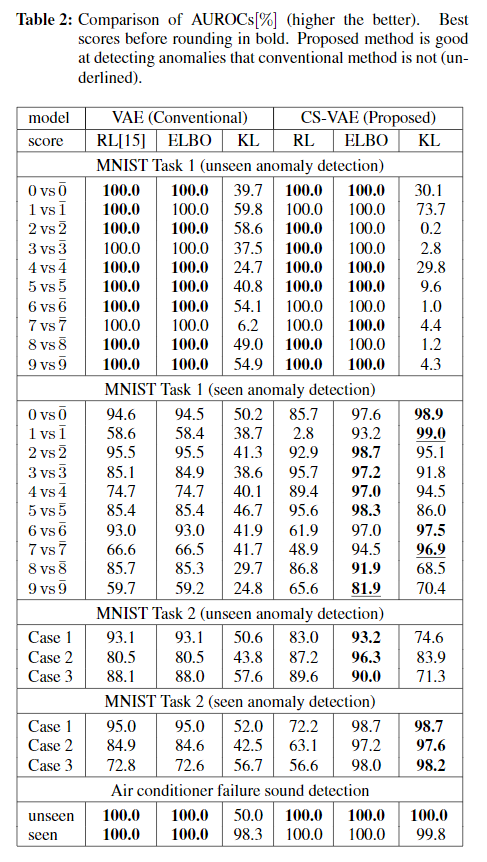
下表为实验结果:
本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!