Anomaly Detection in Streams with Extreme Value Theory

Introduction

本文基于Extreme Value Theory提出了一种不需要手动设置阈值也不需要对数据分布作任何假设的时间序列异常检测方法。除此之外，本方法可以用在通用的自动阈值选择的场合中。

原文

Background

在很多情况下我们需要进行阈值的选择。阈值的选择可以通过实验的方法或者对数据分布进行假设的方法来得到，不过这样做通常不准确。借助Extreme Value Theory我们可以在不需要对原始数据的分布作很强的假设的情况下，推断我们想要的极端事件的分布（在异常检测中就是异常值）。

下面给出一些数学符号，\(X\)为随机变量，\(F\)为累积分布函数，即\(F(x)=\mathbb{P}(X\leq x)\)。记\(F\)的“末尾”分布\(\bar{F}(x)=1-F(x)=\mathbb{P}(X>x)\)。对于一个随机变量\(X\)和给定的概率\(q\)，记\(z_q\)为在\(1-q\)水平的分位数，即\(z_q\)为满足\(\mathbb{P}(X\leq z_q)\geq 1-q\)最小的值。

Extreme Value Distributions

Extreme Value Theory主要是为了找出极端事件发生的规律，有学者证明，在很弱的条件下，所有极端事件都服从一个特定的分布，而不管原始分布如何。具体形式如下：

\[ G_\gamma:x\mapsto \exp(-(1+\gamma x)^{-\frac{1}{\gamma}}), \space\space\space\space\space\gamma\in\mathbb{R}, \space\space\space\space\space 1+\gamma x>0 \]

其中\(\gamma\)称为Extreme Value Index，由原始分布决定。

更严谨的说法是Fisher-Tippett-Gnedenko定理（极值理论第一定理）：

THEOREM: (Fisher-Tippett-Gnedenko). 令\(X_1,X_2,\cdots,X_n,\cdots\)为独立同分布的随机变量序列，\(M_n=\max \{X_1,\cdots,X_n\}\)。如果实数对序列\((a_n,b_n)\)存在且满足\(a_n>0\)和\(\lim\limits_{n\rightarrow \infty}P\left(\frac{M_n-b_n}{a_n}\leq x\right)=F(x)\)，其中\(F\)为非退化分布函数，那么\(F\)属于Gumbel、Fréchet或Weibull分布族（或总称Generalized Extreme Value Distribution）中的一种。

这是一个反直觉的结论，但是想到当事件发生变得极端时，即\(\mathbb{P}(X>x)\rightarrow 0\)，\(\bar{F}(x)=\mathbb{P}(X>x)\)分布的形状其实并没有很多种选择。Table 1展示了几种不同分布对应的\(\gamma\)：

Figure 1展示了几种不同\(\gamma\)情况下的“末尾”分布：

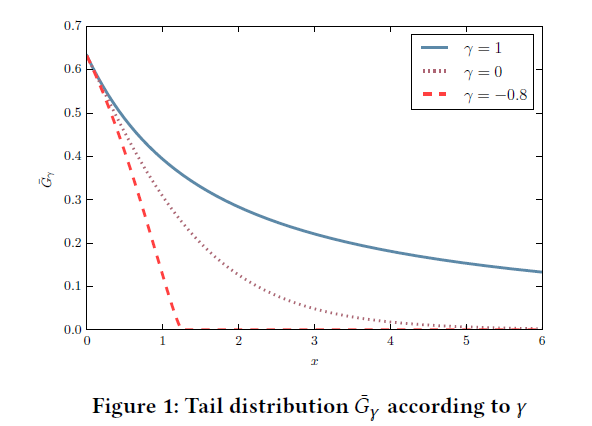
Power of EVT

根据Extreme Value Theory，我们可以在原始分布未知的情况下计算极端事件的概率。但是\(\bar{G}_\gamma\)分布中参数\(\gamma\)是未知的，我们需要一种高效的方法来进行估计。The Peaks-Over-Threshold (POT) 方法是本文介绍的一种方法。

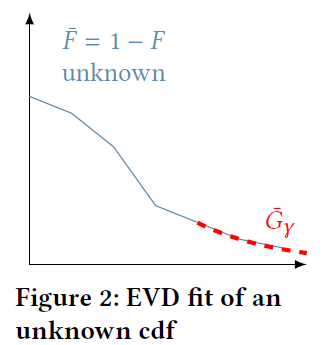
Peaks-Over-Threshold Approach

POT方法依赖于Pickands-Balkema-De Haan定理（极值理论第二定理），维基百科版：

考虑一个未知分布\(F\)和随机变量\(X\)，我们的目标是估计\(X\)在超过确定阈值\(u\)下的条件分布\(F_u\)，定义为： \[ F_u(y)=P(X-u\leq y|X>u)=\frac{F(u+y)-F(u)}{1-F(u)} \] 其中\(0\leq y\leq x_F-u\)，\(x_F\)为\(F\)的右端点。\(F_u\)描述了超过特征阈值\(u\)的分布，称为Conditional Excess Distribution Function。

STATEMENT: (Pickands-Balkema-De Haan). 设\((X_1,X_2,\cdots)\)为独立同分布随机变量序列，\(F_u\)为相应的Conditional Excess Distribution Function。对于一大类的\(F\)和很大的\(u\)，\(F_u\)能够很好的被Generalized Pareto Distribution所拟合： \[ F_u(y)\rightarrow G_{k,\sigma}(y),\space\space \text{as } u\rightarrow \infty \] 其中： \[ G_{k,\sigma}(y)= \begin{cases} 1-(1+ky/\sigma)^{-1/k}, &\text{if }k\neq 0\\ 1-e^{-y/\sigma}, &\text{if }k=0 \end{cases} \] 当\(k\geq 0\)时\(\sigma>0, y\geq 0\)，\(k<0\)时\(0\leq y\leq -\sigma/k\)。

论文中给出的定理如下：

THEOREM: (Pickands-Balkema-De Haan). 累积概率密度函数\(F\in\mathcal{D}_\gamma\)当且仅当函数\(\sigma\)存在时，对所有\(x\in\mathbb{R}\)在\(1+\gamma x>0\)的条件下有： \[ \frac{\bar{F}(t+\sigma(t)x)}{\bar{F}(t)}\mathop{\rightarrow}\limits_{t\rightarrow\tau}(1+\gamma x)^{-\frac{1}{\gamma}} \]

上式可以写成如下形式： \[ \bar{F}_t(x)=\mathbb{P}(X-t>x|X>t)\mathop{\sim}\limits_{t\rightarrow\tau}\left(1+\frac{\gamma x}{\sigma(t)}\right)^{-\frac{1}{\gamma}} \] 该式表明\(X\)超过阈值\(t\)的概率（写为\(X-t\)）服从Generalized Pareto Distribution (GPD)，参数为\(\gamma\)和\(\sigma\)。POT主要是拟合GPD而不是EVT分布。

如果我们要估计参数\(\hat{\gamma}\)和\(\hat{\sigma}\)，分位数可以通过下式计算得到： \[ z_q\simeq t+\frac{\hat{\sigma}}{\hat{\gamma}}\left(\left(\frac{qn}{N_t}\right)^{-\hat{\gamma}}-1\right) \]

其中\(t\)是一个“很高”的阈值，\(q\)是给定的概率值，\(n\)是所有观测样本的数量，\(N_t\)是peaks的数量，即\(X_i>t\)的数量。为了进行高效的参数估计，文中使用了极大似然估计。

Maximum Likelihood Estimation

设\(X_1,\cdots,X_n\)为独立同分布的随机变量，概率密度函数记为\(f_\theta\)，\(\theta\)为分布中的参数，那么似然函数可以写为：

\[ \mathcal{L}(X_1,\cdots,X_n;\theta)=\prod\limits_{i=1}^n f_\theta(X_i) \]

在极大似然估计中，我们需要找到合适的参数使得似然函数最大化。在我们的问题中，似然函数如下： \[ \log\mathcal{L}(\gamma,\sigma)=-N_t\log\sigma-\left(1+\frac{1}{\gamma}\right)\sum\limits_{i=1}^{N_t}\log\left(1+\frac{\gamma}{\sigma}Y_i\right) \] 其中\(Y_i>0\)表示\(X_i\)超过阈值\(t\)的部分。

文中使用了Grimshaw's Trick来将含两个参数的优化问题转换为只含一个参数的优化问题。记\(\ell(\gamma,\sigma)=\log\mathcal{L}(\gamma,\sigma)\)，对于所有极值来说有\(\nabla \ell(\gamma, \sigma)=0\)。Grimshaw's Trick表明对于满足\(\nabla \ell(\gamma, \sigma)=0\)的一对\((\gamma^*,\sigma^*)\)，\(x^*=\frac{\gamma^*}{\sigma^*}\)为等式\(u(X)v(X)=1\)的解，其中： \[ \begin{align} u(x)&=\frac{1}{N_t}\sum\limits_{i=1}^{N_t}\frac{1}{1+xY_i}\\ v(x)&=1+\frac{1}{N_t}\sum\limits_{i=1}^{N_t}\log(1+xY_i) \end{align} \] 在找到满足该等式的解\(x^*\)后，我们可以得到\(\gamma^*=v(x^*)-1\)和\(\sigma^*=\gamma^*/x^*\)，于是问题就变成了如何寻找方程的所有根。

因为\(\log\)的存在，所以有\(1+xY_i>0\)。而\(Y_i\)是正数，所以\(x^*\)的范围一定在\(\left(-\frac{1}{Y^M},+\infty\right)\)，其中\(Y^M=\max Y_i\)。

Grimshaw（作者参考的一篇论文）还给出了一个上界： \[ x^*_{\text{max}}=2\frac{\bar{Y}-Y^m}{(Y^m)^2} \] 其中\(Y^m=\min Y_i\)，\(\bar{Y}\)为\(Y_i\)的均值。详细的优化方法会在下文讨论。

背景部分到此结束，接下来的部分就是作者提出的新方法。

Methodology

Extreme Value Theory给出了在对原始分布未知的情况下估计使得\(\mathbb{P}(X>z_q)<q\)的\(z_q\)的方法。

本文据此提出了时间序列流的异常检测方法。首先根据已知的观测值\(X_1,\cdots,X_n\)得到阈值\(z_q\)，然后根据数据的特性运用两种不同方法来更新\(z_q\)。对于平稳时间序列，使用SPOT；对于非平稳时间序列，使用DSPOT。

Initialization Step

在进行异常检测之前，需要根据已有的观测数据进行\(z_q\)的估计。给定\(n\)个观测值\(X_1,\cdots,X_n\)和一个固定的概率值\(q\)，我们的目标是估计阈值\(z_q\)使得\(\mathbb{P}(X>z_q)<q\)。其主要流程是首先设定一个较大的阈值\(t\)，然后通过拟合GPD分布来计算\(z_q\)。过程如下图所示：

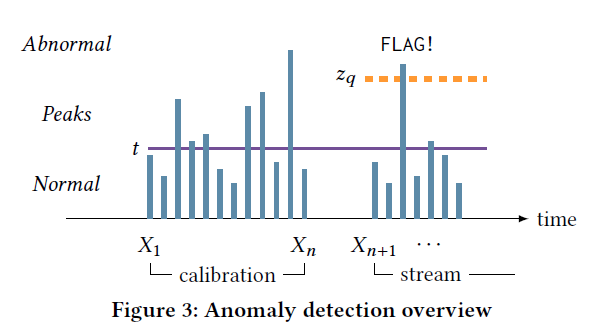
算法流程如下所示：

\(Y_t\)代表大于\(t\)的观测值的集合，GPD分布的拟合使用了前文提到的Grimshaw's Trick。

Finding Anomalies in a Stream

通过Initialization Step使用POT算法得到的\(z_q\)，我们定义其为"Normality Bound"，用于后面的检测。在后面的步骤中，我们会根据新得到的观测值来更新\(z_q\)。

Stationary Case

我们首先来讨论时间序列没有时间依赖性的情况（\(X_1,\cdots,X_n\)之间独立同分布）。通过POT算法对所有观测值得到\(z_q\)之后，Streaming POT (SPOT) 算法会检查\(X_n\)之后的值（数据流场景，\(X_1,\cdots,X_n\)是历史数据，还会有新的数据进来），如果大于\(z_q\)，则将\(X_i\)加入异常点集合中；如果大于\(t\)但小于\(z_q\)，则将\(X_i\)加入观测值集合中，更新\(z_q\)；其他情况我们\(X_i\)是正常情况。算法流程图如下：

Drifting Case

SPOT算法只适用于平稳分布的情况，但在现实生活中这样的假设过强了。于是作者提出了能处理时间依赖性的Streaming POT with Drift (DSPOT) 算法。

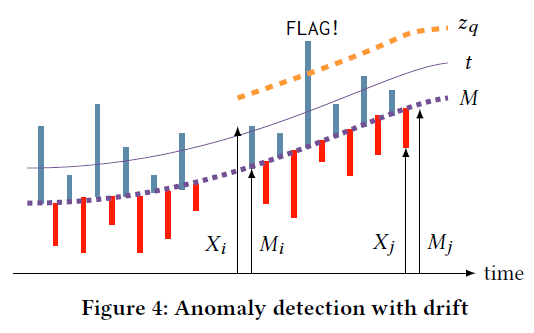
在DSPOT中，我们不使用\(X_i\)的绝对值，而是用相对值\(X^\prime_i=X_i-M_i\)，其中\(M_i\)是\(i\)时刻的局部特征，如Figure 4所示。最简单的实现是使用局部均值，即\(M_i=(1/d)\cdot\sum\limits_{k=1}^d X_{i-k}^*\)，\(X_{i-1}^*,\cdots,X_{i-d}^*\)是长度为\(d\)的窗口。我们假设\(X^\prime_i\)服从平稳分布的假设。

算法流程图如下所示：

Numerical Optimization

现在剩下的问题就是优化了，前文已经提到对GPD的拟合已经被优化成一个参数的优化问题，下面将会详细讨论优化算法。

Reduction of the Optimal Parameters Search

前文已经得到了一个初步的\(x^*\)的Bound，即\(x^*>-\frac{1}{Y^M}\)和\(x^*\leq 2\frac{\bar{Y}-Y^m}{(Y^m)^2}\)，下面将给出一个更严格的Bound。

PROPOSITION: 如果\(x^*\)是\(u(x)v(x)=1\)的解，那么： \[ x^*\leq 0 \text{ or } x^*\geq 2\frac{\bar{Y}-Y^m}{\bar{Y}Y^m} \]

证明见论文原文。

这样\(x^*\)的范围就进一步缩小了，于是有\(u(x)v(X)=1\)的解\(x^*\)在以下范围之内： \[ \left(-\frac{1}{Y^M},0\right]\text{ and }\left[2\frac{\bar{Y}-Y^m}{\bar{Y}Y^m},2\frac{\bar{Y}-Y^m}{(Y^m)^2}\right] \]

How Can We Maximize the Likelihood Function?

接下来是优化的具体实现问题。文中首先设定了一个很小的值\(\epsilon>0\space(\sim 10^{-8})\)，然后在下面的范围内寻找函数\(w:x\mapsto u(x)v(x)-1\)的根： \[ \left[-\frac{1}{Y^M}+\epsilon,-\epsilon\right]\text{ and }\left[2\frac{\bar{Y}-Y^m}{\bar{Y}Y^m},2\frac{\bar{Y}-Y^m}{(Y^m)^2}\right] \] 作者没有使用现有的寻找函数根的算法，而是转换为如下优化问题： \[ \min\limits_{x_1,\cdots,x_k\in I}\sum\limits_{i=1}^k w(x_k)^2 \] 其中\(I\)就是\(x^*\)的Bound。该问题是一个很典型的优化问题，可以被很多成熟的算法所解决。

Initial Threshold

在算法的Initialization Step，需要事先设定一个阈值\(t\)，如果设定的太大，那么\(Y_t\)的数量就会很少。作者给出的建议是保证\(t<z_q\)，即\(t\)对应的概率值应该小于\(1-q\)。

Experiments

在实验部分，作者在合成数据和真实数据上试验了SPOT算法和DSPOT算法的有效性。

(D)SPOT Reliability

作者首先在合成数据上验证SPOT的有效性。具体做法是使用高斯分布生成数据（高斯分布的分位数能够直接计算），然后将SPOT得出的\(z_q\)和理论值进行对比。误差定义如下： \[ \text{error rate}=\left|\frac{z^{\text{SPOT}}-z^{\text{th}}}{z^{\text{th}}}\right| \] 下图是采用不同数量观测值的结果：

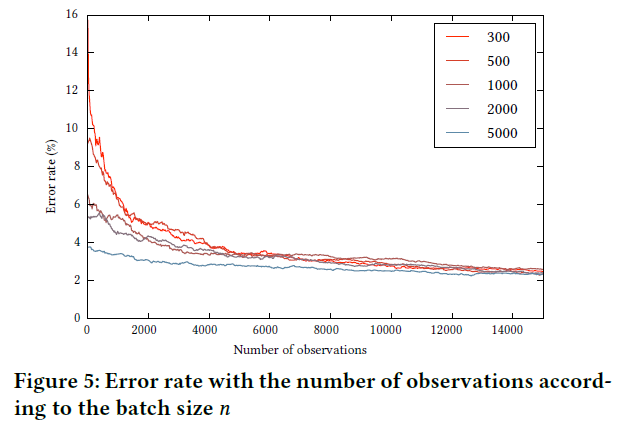
Finding Anomalies with SPOT

在这一节作者在真实数据集上进行了实验以验证SPOT算法的有效性，结果如下图：

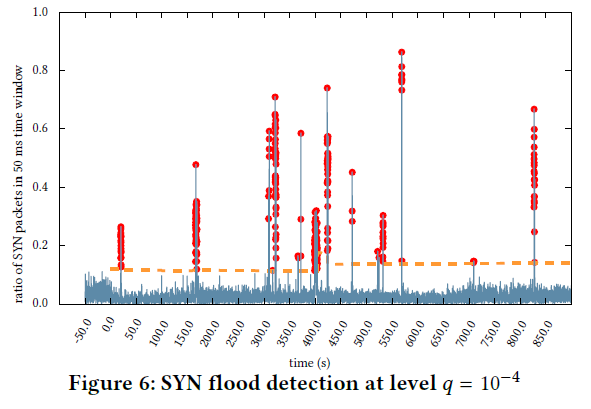
在文中作者说算法的True Positive达到了\(86\%\)，False Positive小于\(4\%\)。

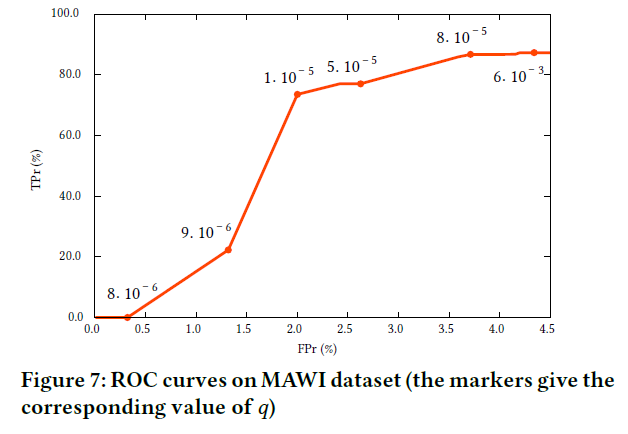
Finding Anomalies with DSPOT

在这一节作者使用DSPOT在真实数据集上进行了实验。窗口大小\(d=450\)，预设的风险概率值\(q=10^{-3}\)。结果如下图所示：

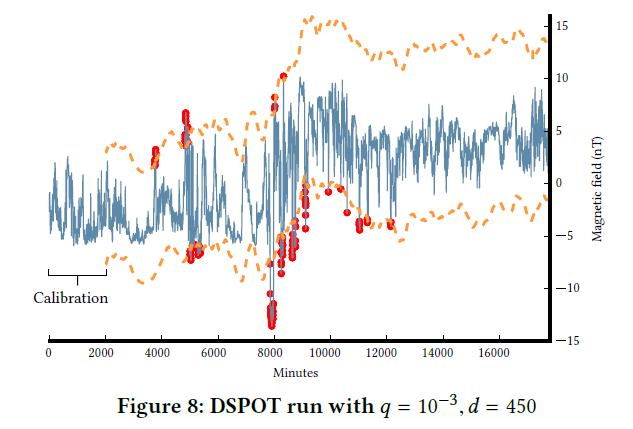
在图中可以看出在\(8000\) Minutes之后上界显著提高，作者分析了原因，认为是因为超过阈值\(t\)的点\(Y_t\)的存储是全局的，在前\(8000\) Minutes算法存储了很多较高的\(Y_t\)值，而在\(8000\) Minutes之后，真实数据的趋势开始下降，但算法仍是根据全局的\(Y_t\)来进行\(z_q\)的计算（这一段没有特别明白）。作者给出的修正方法是只保存固定数量的Peaks。

下图是作者在股票数据上得到的实验结果：

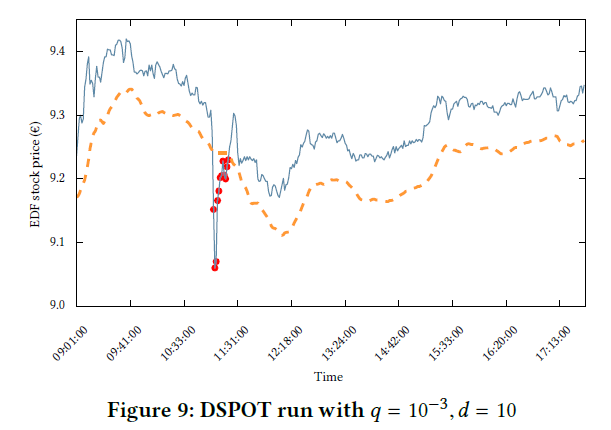
Performances

作者还验证了算法的时间效率。

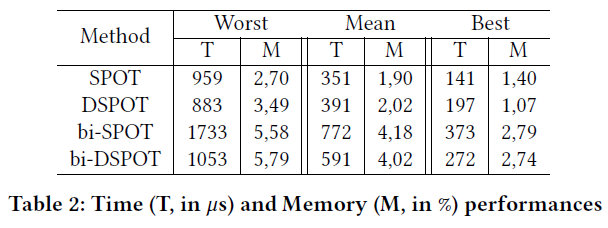
表中T代表的是每个Iteration的时间，M代表的是Peaks的比例，"bi-"前缀代表的是同时计算上界和下界。