An Introduction to Variational Autoencoders
本文最后更新于:2 年前
Deep Generative Models
生成模型是指一系列用于随机生成可观测数据的模型。假设在一个高维空间\(\mathcal{X}\)中,存在一个随机向量\(\mathbf{X}\)服从一个未知的分布\(p_r(x),x\in \mathcal{X}\)。生成模型就是根据一些可观测的样本\(x^{(1)},x^{(2)},\cdots,x^{(N)}\)来学习一个参数化的模型\(p_\theta(x)\)来近似未知分布\(p_r(x)\)。
生成模型主要用于密度估计和样本生成。
密度估计即给定一组数据\(\mathcal{D}=\{x^{(i)}\},1\leq i\leq N\),假设他们都是从相同的概率密度函数\(p_r(x)\)独立产生的。密度估计就是根据数据集\(\mathcal{D}\)来估计其概率密度函数\(p_r(x)\)。
如果将生成模型用于监督学习,那么就是输出标签的条件概率分布\(p(y|x)\),根据贝叶斯公式:
\[p(y|x)=\frac{p(x,y)}{\sum_y p(x,y)}\]
问题就变为了联合概率\(p(x,y)\)的密度估计问题。
样本生成即根据给定的概率分布\(p_\theta(x)\)生成一些服从这个分布的样本,即采样。在含隐变量的生成模型中,生成\(x\)的过程一般包含两步:
- 根据隐变量的分布\(p_\theta(z)\)采样得到\(z\);
- 根据条件分布\(p_\theta(x|z;\theta)\)进行采样得到\(x\)。
所以在生成模型中的重点是估计条件分布\(p(x|z;\theta)\)。
Parameter Estimation for Hidden Variable with EM Algorithm
如果图模型中存在隐变量,就需要使用EM算法进行参数估计。
在一个包含隐变量的图模型中,令\(\mathbf{X}\)为可观测变量集合,\(\mathbf{Z}\)为隐变量集合,则一个样本\(x\)的边际似然函数为:
\[p(x;\theta)=\sum_z p(x,z;\theta)\]
给定包含\(N\)个训练样本的训练集\(\mathcal{D}=\{x^{(n)}\},1\leq i\leq N\),则训练集的对数边际似然为:
\[\begin{align}\mathcal{L}(\mathcal{D};\theta)&=\frac{1}{N}\sum_{n=1}^N \log p(x^{(n)};\theta)\\&=\frac{1}{N}\sum_{n=1}^N \log \sum_z p(x^{(n)},z;\theta)\end{align}\]
这时,只要最大化整个训练集的对数边际似然\(\mathcal{L}(\mathcal{D};\theta)\),即可估计出最优的参数\(\theta^*\)。不过在计算梯度的时候,需要在对数函数内部进行求和或积分计算。为了更好的计算\(\log p(x;\theta)\),我们引入一个额外的变分函数\(q(z)\),\(q(z)\)为定义在隐变量\(z\)上的分布。样本\(x\)的对数边际似然函数为:
\[\begin{align}\log p(x;\theta)&=\log \sum_z q(z)\frac{p(x,z;\theta)}{q(z)}\\&\geq\sum_z q(z)\log \frac{p(x,z;\theta)}{q(z)}\\&\triangleq ELBO(q,x;\theta)\end{align}\]
其中\(ELBO(q,x;\theta)\)为对数边际似然函数\(\log p(x;\theta)\)的下界,称为证据下界。公式中使用了Jensen不等式(即对于凹函数\(g\),有\(g(\mathbb{E}[x])\geq\mathbb{E}[g(X)]\))。在这里,\(\frac{p(x,z;\theta)}{q(z)}\)可视为\(q(z)\)的函数,记为\(f(q(z))\),那么\(f(q(z))\)的期望即\(\mathbb{E}[f(q(z))]=\sum_z q(z)f(q(z))=\sum_z q(z)\frac{p(x,z;\theta)}{q(z)}\)。而根据Jensen不等式,有\(g(\mathbb{E}[f(q(z))])\geq\mathbb{E}[g(f(q(z)))]\Leftrightarrow g(\sum_z q(z)\frac{p(x,z;\theta)}{q(z)})\geq \sum_z q(z)g(\frac{p(x,z;\theta)}{q(z)})\),在这里\(g\)就是对数函数。
根据Jensen不等式取等的条件:\(\frac{p(x,z;\theta)}{q(z)}=c\),\(c\)为常数,有:
\[\begin{align}\sum_z p(x,z;\theta)&=c\sum_z q(z)\\\Leftrightarrow\sum_z p(x,z;\theta)&=c\cdot1\end{align}\]
因此:
\[\begin{align}q(z)&=\frac{p(x,z;\theta)}{\sum_z p(x,z;\theta)}\\&=\frac{p(x,z;\theta)}{p(x;\theta)}\\&=p(z|x;\theta)\end{align}\]
所以,当且仅当\(q(z)=p(z|x;\theta)\)时,\(\log p(x;\theta)=ELBO(q,x;\theta)\)。
于是最大化对数边际似然函数\(\log p(x;\theta)\)的过程可以分解为两个步骤:
- 先找到近似分布\(q(z)\)使得\(\log p(x;\theta)=ELBO(q,x;\theta)\);
- 再寻找参数\(\theta\)最大化\(ELBO(q,x;\theta)\)。
这就是期望最大化(Expectation-Maximum,EM)算法。
EM算法通过迭代的方法,不断重复直到收敛到某个局部最优解。在第\(t\)步更新时,E步和M步分别为:
E步:固定参数\(\theta_t\),找到一个分布使\(ELBO(q,x;\theta_t)\)最大,即等于\(\log p(x;\theta_t)\):\(q_{t+1}(z)=\text{arg}_q \max ELBO(q,x;\theta_t)\);
M步:固定\(q_{t+1}(z)\),找到一组参数使得证据下界最大,即:\(\theta_{t+1}=\text{arg}_\theta\max ELBO(q_{t+1},x;\theta)\)。
对数边际似然也可以通过信息论的视角来进行分解:
\[\begin{align}\log p(x;\theta)&=\sum_z q(z)\log p(x;\theta)\\&=\sum_z q(z)(\log p(x,z;\theta)-\log p(z|x;\theta))\\&=\sum_z q(z)\log\frac{p(x,z;\theta)}{q(z)}-\sum_z q(z)\log\frac{p(z|x;\theta)}{q(z)}\\&=ELBO(q,x;\theta)+D_{KL}(q(z)\parallel p(z|x;\theta))\end{align}\]
其中\(D_{KL}(q(z)\parallel p(z|x;\theta))\)
Generative Model with Hidden Variable
假设一个生成模型包含不可观测的隐变量,其中可观测变量\(x\)为一个高维空间中的随机向量,而不可观测的隐变量\(z\)为一个相对低维空间中的随机向量。
这个生成模型的联合概率密度函数可以表达为:
\[p(x,z;\theta)=p(x|z;\theta)p(z;\theta)\]
其中\(p(z;\theta)\)为隐变量\(z\)的先验概率分布;\(p(x|z;\theta)\)为已知\(z\)条件下\(x\)的概率分布。通常情况下,我们可以假设\(p(z;\theta)\)和\(p(x|z;\theta)\)服从某种带参的分布族,其形式已知,而参数可以通过最大似然来进行估计。
给定一个样本\(x\),其对数边际似然\(\log p(x;\theta)\)可以分解为:
\[\log p(x;\theta)=ELBO(q,x;\theta,\phi)+D_{KL}(q(z;\phi)\parallel p(z|x;\theta))\]
其中\(q(z;\phi)\)为额外引入的变分密度函数,\(ELBO(q,x;\theta,\phi)\)为证据下界:
\[ELBO(q,x;\theta,\phi)=\mathbb{E}_{z\sim q(z;\phi)}[\log{\frac{p(x,z;\theta)}{q(z;\phi)}}]\]
最大化\(\log p(x;\theta)\)可以用EM算法来求解:
- E-step: 寻找一个密度函数\(q(z;\phi)\)使其等于或接近于后验密度函数\(p(z|x;\theta)\);
- M-step: 保持\(q(z;\phi)\)固定,寻找\(\theta\)来最大化\(ELBO(q,x;\theta,\phi)\)。
在EM算法的每次迭代中,理论上最优的\(q(z;\phi)\)为隐变量的后验概率密度函数\(p(z|x;\theta)\):
\[p(z|x;\theta)=\frac{p(x|z;\theta)p(z;\theta)}{\int_z p(x|z;\theta)p(z;\theta)\text{d}z}\]
后验密度函数\(p(z|x;\theta)\)的计算是一个统计推断的问题,在一般情况下\(p(x|z;\theta)\)也比较难以计算。
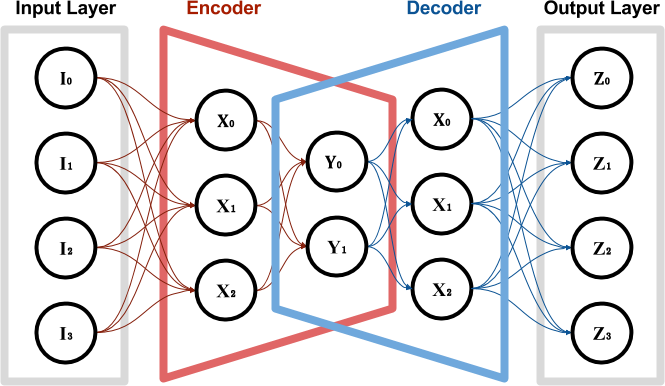
Variational Autoencoder
变分自编码器(Variational Autoencoder, VAE)的主要思想是利用神经网络来分别建模两个复杂的条件概率密度函数:
- 用神经网络来产生变分分布\(q(z;\phi)\),称为推断网络。推断网络的输入为\(x\),输出为变分分布\(q(z|x;\phi)\);
- 用神经网络来产生概率分布\(p(x|z;\theta)\),称为生成网络。生成网络的输入为\(z\),输出为概率分布\(p(x|z;\theta)\)。
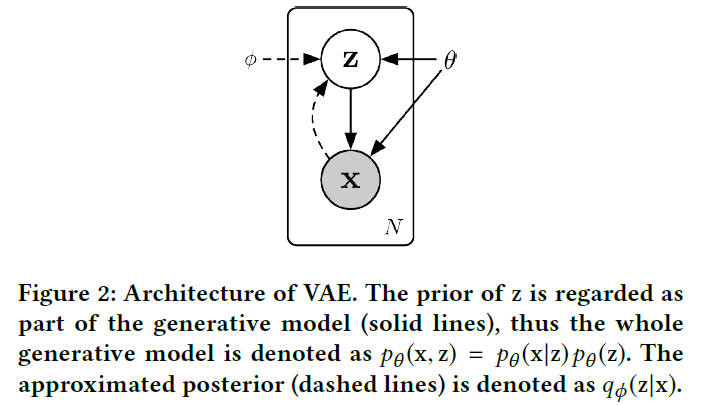
VAE的图模型如下图所示:
Variational Network
假设\(q(z|x;\phi)\)是服从对角化协方差的高斯分布:
\[q(z|x;\phi)=\mathcal{N}(z;\mu_I,\sigma^2_I I)\]
其中\(\mu_I\)和\(\sigma_I^2\)是高斯分布的均值和方差,可以通过推断网络\(f_I(x;\phi)\)来预测:
\[ \left[\begin{matrix}\mu_I\\\sigma_I\end{matrix}\right]=f_I(x;\phi) \] 推断网络\(f_I(x;\phi)\)可以是一般的全连接网络或卷积网络,比如一个两层的神经网络:
\[\begin{align}h&=\sigma(W^{(1)}x+b^{(1)})\\\mu_I&=W^{(2)}h+b^{(2)}\\\sigma_I&=\text{softplus}(W^{(3)}h+b^{(3)})\end{align}\]
其中所有网络参数\(\{W^{(1)},W^{(2)},W^{(3)},b^{(1)},b^{(2)},b^{(3)}\}\)即对应了变分参数\(\phi\)。
推断网络的目标是使得\(q(z|x;\phi)\)来尽可能接近真实的后验\(p(z|x;\theta)\),需要找到变分参数\(\phi^*\)来最小化两个分布的KL散度:
\[\phi^*=\text{arg}_\phi\min{D_{KL}(q(z|x;\phi)\parallel p(z|x;\theta))}\]
由于\(p(z|x;\theta)\)未知,故KL散度无法直接计算,不过由于\(D_{KL}(q(z|x;\phi)\parallel p(z|x;\theta))=\log p(x;\theta)-ELBO(q,x;\theta,\phi)\),所以可以直接最大化证据下界,有:
\[\phi^*=\text{arg}_\phi\max{ELBO(q,x;\theta,\phi)}\]
Generative Network
生成模型的联合分布可以分解为两部分:隐变量\(z\)的先验分布\(p(z;\theta)\)和条件概率分布\(p(x|z;\theta)\)。为简单起见,一般假设隐变量\(z\)的先验分布为标准正态分布\(\mathcal{N}(z|0,I)\),隐变量每一维之间都是独立的。条件概率分布\(p(x|z;\theta)\)可以通过生成网络来建模,我们同样用参数化的分布族来表示条件概率分布\(p(x|z;\theta)\),这些分布族的函数可以用生成网络计算得到。根据变量\(x\)的类型不同,可以假设\(p(x|z;\theta)\)服从不同的分布族。如果\(x\in\{0,1\}^d\)是\(d\)维的二值向量,可以假设\(\log p(x|z;\theta)\)服从多变量的伯努利分布,即:
\[\begin{align}p(x|z;\theta)&=\prod\limits_{i=1}^d p(x_i|z;\theta)\\&=\prod\limits_{i=1}^d \gamma_i^{x_i}(1-\gamma_i)^{(1-x_i)}\end{align}\]
如果\(x\in\mathbb{R}^d\)是\(d\)维的连续向量,可以假设\(p(x|z;\theta)\)服从对角化协方差的高斯分布,即:
\[p(x|z;\theta)=\mathcal{N}(x;\mu_G,\sigma_G^2 I)\]
生成网络的目标是找到一组\(\theta^*\)最大化证据下界\(ELBO(q,x;\theta,\phi)\):
\[\theta^*=\text{arg}_\theta\max ELBO(q,x;\theta,\phi)\]
Model Combination
推断网络和生成网络的目标都是最大化证据下界因此总的目标函数为:
\[\begin{align}\max_{\theta,\phi}ELBO(q,x;\theta,\phi)&=\max_{\theta,\phi}\mathbb{E}_{z\sim q(z;\phi)}[\log\frac{p(x|z;\theta)p(z;\theta)}{q(z;\theta)}]\\&=\max_{\theta,\phi}\mathbb{E}_{z\sim q(z|x;\phi)}[\log p(x|z;\theta)]-D_{KL}(q(z|x;\phi)\parallel p(z;\theta))\end{align}\]
其中先验分布\(p(z;\theta)=\mathcal{N}(z|0,I)\)。
公式中\(\mathbb{E}_{z\sim q(z|x;\phi)}[\log p(x|z;\theta)]\)一般通过采样的方式进行计算,最后取平均值。
Model Training
给定数据集\(\mathcal{D}\),包含\(N\)个从未知数据分布中抽取的独立同分布样本\(x^{(1)},x^{(2)},\cdots,x^{(N)}\)。变分自编码器的目标函数为:
\[\mathcal{J}(\phi,\theta|\mathcal{D})=\sum\limits_{n=1}^N(\frac{1}{M}\sum\limits_{m=1}^M\log p(x^{(n)}|z^{(n,m)};\theta)-D_{KL}(q(z|x^{(n)};\phi)\parallel\mathcal{N}(z;0,I)))\]
如果采用随机梯度下降法,每次从数据集中采一个样本\(x\),然后根据\(q(z|x;\phi)\)采一个隐变量\(z\),则目标函数变为:
\[\mathcal{J}(\phi,\theta|x)=\log p(x|z;\theta)-D_{KL}(q(z|x;\phi)\parallel\mathcal{N}(z;0,I))\]
假设\(q(z|x;\phi)\)是正态分布,KL散度可直接算出:
\[D_{KL}(\mathcal{N}(\mu_1,\Sigma_1)\parallel\mathcal(\mu_2,\Sigma_2))\\=\frac{1}{2}(\text{tr}(\sigma_I^2 I)+\mu_I^T\mu_I-d-\log(|\sigma_I^2 I|))\]
再参数化是将一个参数为\(u\)的函数\(f(u)\),通过一个函数\(u=g(v)\),转换为参数为\(v\)的函数\(\hat{f}(v)=f(g(v))\)。在变分自编码器中,一个问题是如何求随机变量\(z\)关于\(\phi\)的导数。但由于是采样的方式,无法直接刻画\(z\)和\(\phi\)之间的函数关系,因此也无法计算导数。
如果\(z\sim q(z|x;\phi)\)的随机性独立于参数\(\phi\),我们可以通过再参数化的方法来计算导数。假设\(q(z|x;\phi)\)为正态分布\(\mathcal{N}(\mu_I,\sigma^2_I I)\),其中\(\mu_I\)和\(\sigma_I\)是推断网络\(f_I(x;\phi)\)的输出。我们可以通过下面的方式采样\(z\):
\[z=\mu_I+\sigma_I\odot \varepsilon\]
其中\(\varepsilon\sim\mathcal{N}(0,I)\)。这样\(z\)和\(\mu_I,\sigma_I\)的关系从采样关系变为函数关系。
如果进一步假设\(p(x|z;\theta)\)服从高斯分布\(\mathcal{N}(x|\mu_G,I)\),其中\(\mu_G=f_G(z;\theta)\)是生成网络的输出,则目标函数可以简化为:
\[\mathcal{J}(\phi,\theta|x)=-\parallel x-\mu_G\parallel^2+D_{KL}(\mathcal{N}(\mu_I,\sigma_I)\parallel\mathcal{N}(0,I))\]
其中第一项可以近似看作是输入\(x\)的重构正确性,第二项可以看作是正则化项。
本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!