Robust Anomaly Detection for Multivariate Time Series through Stochastic Recurrent Neural Network
本文最后更新于:1 年前
Abstract
本文提出了OmniAnomaly:一种针对多变量时间序列的随机循环神经网络异常检测算法。该模型运用了一系列技术来捕捉多变量时间序列的正常模式,并在检测阶段基于重构误差来检测异常,同时本文还提供了一定的理论解释。
Contribution
- 提出了OmniAnomaly,一种基于随机循环神经网络的多变量时间序列异常检测算法;
- 提出了针对多变量时间序列异常检测的解释方法;
- 通过实验证明了OmniAnomaly中所用的关键技术的有效性,包括GRU,planar NF, stochastic variable connection和adjusted Peaks-Over-Threshold method;
- 通过大量的实验我们证明了OmniAnomaly的有效性;
- 发布了代码和数据集。
Background
Linear Gaussian State Space Model
状态空间模型(State Space Model, SSM)的概念来自于控制理论,在这里我们主要讨论其在时间序列中的应用。其大概思想是我们认为时间序列在时刻\(t\)的观测值\(z_t\)是一个隐含状态\(\boldsymbol{l}_t\)的条件分布\(p(z_t|\boldsymbol{l}_t)\),而这个隐含状态\(\boldsymbol{l}_t\)刻画了时间序列的内在规律,同时隐含状态会随着时间更新,即服从条件分布\(p(\boldsymbol{l}_t|\boldsymbol{l}_{t-1})\)。
在线性状态空间模型(Linear State Space Model)中我们以如下的方式刻画隐含状态的更新: \[ \boldsymbol{l}_t=\boldsymbol{F}_t\boldsymbol{l}_{t-1}+\boldsymbol{g}_t\varepsilon_t, \space\space\space\varepsilon_t\sim\mathcal{N}(0,1) \] \(\boldsymbol{F}_t\)为确定的状态转移矩阵,而\(\boldsymbol{g}_t\varepsilon_t\)则表示了状态转移的随机性。
观测值\(z_t\)从隐含状态\(\boldsymbol{l}_t\)计算而来: \[ \begin{align} z_t&=y_t+\sigma_t\epsilon_t,\\ y_t&=\boldsymbol{a}_t^\top\boldsymbol{l}_{t-1}+b_t,\\ \epsilon_t&\sim\mathcal{N}(0,1) \end{align} \] 其中\(\boldsymbol{a}_t\in\mathbb{R}^L,\sigma_t\in \mathbb{R},b_t\in\mathbb{R}\)都是额外的参数。初始状态\(\boldsymbol{l}_0\)则从一个独立的高斯分布得来,即\(\boldsymbol{l}_0\sim N(\boldsymbol\mu_0,\text{diag}(\boldsymbol{\sigma}_0^2))\)。
令参数集合\(\Theta_t=(\boldsymbol{\mu}_0,\boldsymbol{\Sigma}_0,\boldsymbol{F}_t,\boldsymbol{g}_t,\boldsymbol{a}_t,b_t,\sigma_t),\forall t>0\),一般来说参数集合不会随着时间变化,即每个时刻\(t\)共享同样的参数\(\Theta_t=\Theta,\forall t>0\)。对参数的估计可以采用极大似然估计: \[ \begin{align} \Theta^*_{1:T}&=\arg\max_{\Theta_{1:T}}p(z_{1:T}|\Theta_{1:T}),\\ \end{align} \] 其中: \[ \begin{align} p(z_{1:T}|\Theta_{1:T})&=p(z_1|\Theta_1)\prod\limits_{t=2}^T p(z_t|z_{1:t-1},\Theta_{1:t})\\ &=\int p(\boldsymbol{l}_0)\left[\prod\limits_{t=1}^T p(z_t|\boldsymbol{l}_t)p(\boldsymbol{l}_t|\boldsymbol{l}_{t-1})\right]\mathrm{d}\boldsymbol{l}_{0:T} \end{align} \]
Planar Normalizing Flow
Normalizing Flows
VAE采用一个变分分布\(q_\phi(z|x)\)来近似真实的后验分布\(p(z|x)\),并推导出\(\log p_\theta(x)\)的下界(称为ELBO)来作为优化目标函数: \[ \begin{align} \log p_\theta(x)&=\log \int p_\theta(x|z)p(z)\mathrm{d}z\\ &=\log\int\frac{q_\phi(z|x)}{q_\phi(z|x)}p_\theta(x|z)p(z)\mathrm{d}z\\ &\geq-D_{KL}[q_\phi(z|x)\parallel p(z)]+\mathbb{E}_q[\log p_\theta(x|z)] \end{align} \] \(\log p_\theta(x)\)与ELBO取等的条件是\(D_{KL}[q_\phi(z|x)\parallel p(z)]\),表明变分分布完全匹配了真实的后验分布。但在实际应用中,真实的后验分布可能会非常复杂,而我们的变分分布通常是一个确定的较为简单的分布,如高斯分布。这样变分分布可能很难对真实后验分布得到一个很好的拟合。
一个解决方案是使用标准化流(Normalizing Flows)。标准化流是从一个相对简单的分布出发,执行一系列可逆的映射,将原始简单的分布转化为一个复杂的分布。
首先考虑一个光滑的、可逆的映射\(f:\mathbb{R}^d\mapsto \mathbb{R}^d\),记\(g=f^{-1}\),那么\(g\circ f(\mathbf{z})=\mathbf{z}\)。令\(\mathbf{z}^\prime=f(\mathbf{z})\),那么\(\mathbf{z}^\prime\)的分布为: \[ q(\mathbf{z}^\prime)=q(\mathbf{z})\left|\text{det}\frac{\partial f^{-1}}{\partial \mathbf{z}^\prime}\right|=q(z)\left|\text{det}\frac{\partial f}{\partial \mathbf{z}}\right|^{-1} \] 式中\(q(\mathbf{z}^\prime)=q(z)\left|\text{det}\frac{\partial f}{\partial \mathbf{z}}\right|^{-1}\)说明了\(\mathbf{z}^\prime\)的分布等于\(\mathbf{z}\)的分布乘上\(f\)的Jacobian矩阵的行列式的倒数。那么对于映射多次的情况: \[ \mathbf{z}_K=f_K\circ\cdots\circ f_2\circ f_1(\mathbf{z}_0) \] \(\mathbf{z}_K\)的分布可以通过链式计算得到: \[ \ln q_K(\mathbf{z}_K)=\ln q_0(\mathbf{z}_0)-\sum\limits_{k=1}^K\ln\left|\text{det}\frac{\partial f_k}{\partial \mathbf{z}_{k-1}}\right| \]
Planar Flows
考虑一个变换族: \[ f(\mathbf{z})=\mathbf{z}+\mathbf{u}h(\mathbf{w}^\top\mathbf{z}+b) \] 其中\(\lambda=\{\mathbf{w}\in \mathbb{R}^d,\mathbf{u}\in\mathbb{R}^d,b\in\mathbb{R}\}\)为参数集合,\(h(\cdot)\)为元素级的非线性函数(如各种激活函数)。令\(\psi(\mathbf{z})=h^\prime(\mathbf{w}^\top\mathbf{z}+b)\mathbf{w}\),则\(f\)的Jacobian矩阵行列式绝对值等于: \[ \left|\text{det}\frac{\partial f}{\partial \mathbf{z}}\right|=\left|\text{det}(\mathbf{I}+\mathbf{u}\psi(\mathbf{z})^\top)\right|=\left|1+\mathbf{u}^\top\psi(\mathbf{z})\right| \] 但是\(f\)并不保证总是可逆的,如\(h(x)=\tanh(x)\)时,\(f\)可逆的条件是\(\mathbf{w}^\top \mathbf{u}\geq-1\)。
下面讨论如何保证可逆的条件。考虑将\(\mathbf{z}\)分解为\(\mathbf{z}=\mathbf{z}_\bot+\mathbf{z}_\parallel\),其中\(\mathbf{z}_\bot\)与\(\mathbf{w}\)正交,\(\mathbf{z}_\parallel\)与\(\mathbf{w}\)平行,那么: \[ f(z)=\mathbf{z}_\bot+\mathbf{z}_\parallel+\mathbf{u}h(\mathbf{w}^\top \mathbf{z}_\parallel +b) \] 实际上得到\(\mathbf{z}_\parallel\)之后可以很容易的得到\(\mathbf{z}_\bot\),令\(\mathbf{y}=f(\mathbf{z})\),有: \[ \mathbf{z}_\bot=\mathbf{y}-\mathbf{z}_\parallel-\mathbf{u}h(\mathbf{w}^\top\mathbf{z}_\parallel+b) \] 而\(\mathbf{z}_\parallel\)与\(\mathbf{w}\)平行,易知\(\mathbf{z}_\parallel=\alpha\frac{\mathbf{w}}{\parallel\mathbf{w}\parallel^2}\),其中\(\alpha\in\mathbb{R}\)。
对式(16)两边同时乘以\(\mathbf{w}^\top\)可得: \[ \mathbf{w}^\top f(\mathbf{z})=\alpha+\mathbf{w}^\top\mathbf{u} h(\alpha+b) \] 当\(\alpha+\mathbf{w}^\top\mathbf{u} h(\alpha+b)\)对于\(\alpha\)是非递减函数的时候,\(f\)是可逆的。因为\(\alpha+\mathbf{w}^\top\mathbf{u} h(\alpha+b)\)是非递减函数时有\(1+\mathbf{w}^\top\mathbf{u}h^\prime(\alpha+b)\geq 0\equiv \mathbf{w}^\top \mathbf{u}\geq -\frac{1}{h^\prime(\alpha + b)}\),而\(0\leq h^\prime(\alpha + b) \leq 1\)(\(\tanh\)函数的性质),所以总是有\(\mathbf{w}^\top \mathbf{u}\geq-1\)。
对于任意一个\(\mathbf{u}\),我们可以通过特定的方式构造一个\(\hat{\mathbf{u}}\)使得\(\mathbf{w}^\top\hat{\mathbf{u}}>-1\),即令\(\hat{\mathbf{u}}(\mathbf{w},\mathbf{u})=\mathbf{u}+[m(\mathbf{w}^\top\mathbf{u})-(\mathbf{w}^\top\mathbf{u})]\frac{\mathbf{w}}{\parallel\mathbf{w}\parallel^2}\),其中\(m(x)=-1+\log(1+e^x)\)。

Methodology
Problem Statement
本文针对的是多变量时间序列\(x=\{x_1,x_2,\cdots,x_N\}\in R^{M\times N}\),\(N\)为时间长度,其中某一时刻的观测值\(x_t\in R^M\)为一个\(M\)维的向量。作者使用\(x_{t-T:t}\in R^{M\times(T+1)}\)来表示\(t-T\)到\(t\)之间的时间序列。
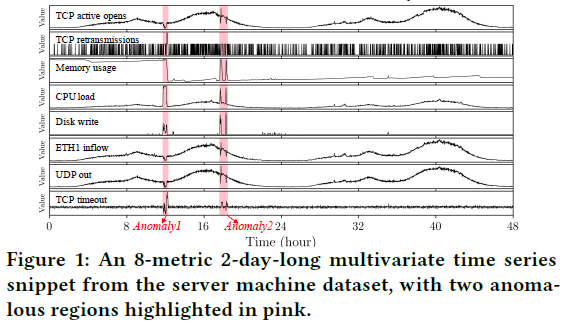
Overall Structure
算法的总体框架如下图所示:
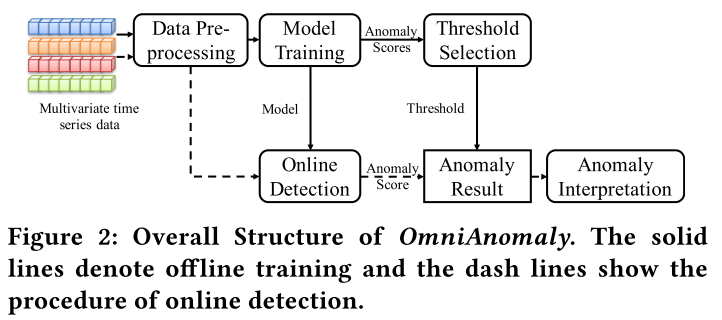
预处理模块主要是对数据进行标准化以及窗口切分。训练模块则根据输入的数据对正常模式进行捕捉,输出异常分数。在线检测模块则会定期执行。
Network Architecture
模型的总体结构如下图所示:
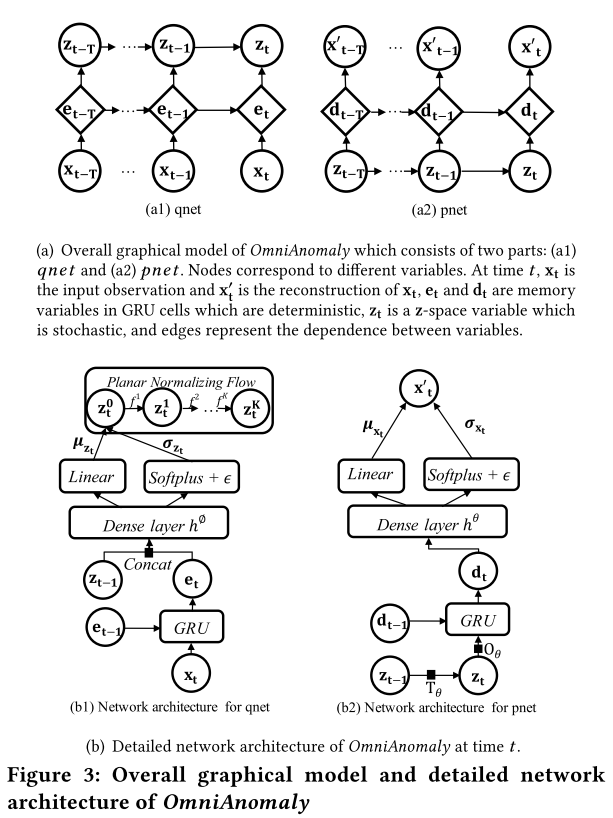
在qnet中,首先GRU被用来建模样本的时间依赖关系,之后VAE将样本\(\mathbf{x}\)映射到隐空间\(\mathbf{z}\)。文中使用了Linear Gaussian State Space Model来建模隐变量之间的时间依赖关系。除此之外,作者还使用了Planar Normalizing Flow来将隐变量映射到复杂的非高斯分布。在pnet中,隐变量\(\mathbf{z}_{t-T:t}\)被用来重建\(\mathbf{x}_{t-T:t}\),直观上来说,对样本的好的隐变量表示可以带来更好的重构效果。
从细节上来说,在时间\(t\),qnet的输入为\(\mathbf{x}_t\)和\(\mathbf{e}_{t-1}\),两者经过GRU Cell之后会产生\(t\)时间的\(\mathbf{e_t}\)。\(\mathbf{e}_t\)是GRU捕捉时间依赖性的关键,可以认为它包含了\(\mathbf{x}_{1:t}\)的信息。之后\(\mathbf{e}_t\)会和\(\mathbf{z}_{t-1}\)进行拼接,进入标准的VAE变分网络结构,通过网络输出的参数\(\mu_{z_t},\sigma_{z_t}\)采样得到隐变量\(\mathbf{z}_t^0\),此时隐变量可以说捕捉了时间依赖性。
网络中涉及到的公式如下所示:
\[ \begin{align} e_t&=(1-c_t^e)\circ\text{tanh}(w^ex_t+u^e(r_t^e\circ e_{t-1})+b^e)+c_t^e\circ e_{t-1}\\ \mu_{z_t}&=w^{\mu_z}h^\phi([z_{t-1},e_t])+b^{\mu_z}\\ \sigma_{z_t}&=\text{softplus}(w^{\sigma_z}h^\phi([z_{t-1},e_t])+b^{\sigma_z})+\epsilon^{\sigma_z} \end{align} \]
其中\(r_t^e=\text{sigmoid}(\mathbf{w}^{r^e}\mathbf{x}_t+\mathbf{u}^{r^e}\mathbf{e}_{t-1}+b^{r^e})\)是GRU中的重置门,\(c_t^e=\text{sigmoid}(\mathbf{w}^{c^e}\mathbf{x}_t+\mathbf{u}^{c^e}\mathbf{e}_{t-1}+b^{c^e})\)是GRU中的更新门。
此时\(\mathbf{z}_t^0\)服从高斯分布,为了拟合复杂的后验分布,我们使用Planar Normalizing Flow来对\(\mathbf{z}_t^0\)进行变换,最后得到经\(K\)次变换后的随机变量\(\mathbf{z}_t^K\)。
在时间\(t\),pnet试图通过\(\mathbf{z}_t^K\)来重构\(\mathbf{x}_t\)。首先\(\mathbf{z}\)空间中的变量会根据Linear Gaussian State Space Model来进行“连接“,公式为\(\mathbf{z}_t=\mathbf{O}_\theta(\mathbf{T}_\theta\mathbf{z}_{t-1}+\mathbf{v}_t)+\boldsymbol{\epsilon}_t\),其中\(\mathbf{O}_\theta\)和\(\mathbf{T}_\theta\)为状态转移矩阵,\(\mathbf{v}_t\)和\(\boldsymbol{\epsilon}_t\)为随机噪声。之后\(\mathbf{z}_t\)和\(\mathbf{d}_{t-1}\)会作为GRU的输入,产生\(\mathbf{d}_t\)。之后\(\mathbf{d}_t\)会经过标准VAE中的生成网络,通过网络输出的高斯分布参数\(\mu_{x_t},\sigma_{x_t}\)采样得到重构后的样本\(\mathbf{x}^\prime_t\)。pnet中涉及到的公式如下所示: \[ \begin{align} d_t&=(1-c_t^d)\circ\text{tanh}(w^dz_t+u^d(r_t^d\circ d_{t-1})+b^d)+c_t^d\circ d_{t-1}\\ \mu_{x_t}&=w^{\mu_x}h^\theta(d_t)+b^{\mu_x}\\ \sigma_{x_t}&=\text{softplus}(w^{\sigma_x}h^\theta(d_t)+b^{\sigma_x})+\epsilon^{\sigma_x} \end{align} \]
其中\(r_t^d=\text{sigmoid}(\mathbf{w}^{r^d}\mathbf{x}_t+\mathbf{u}^{r^d}\mathbf{d}_{t-1}+b^{r^d})\)是GRU中的重置门,\(c_t^d=\text{sigmoid}(\mathbf{w}^{c^d}\mathbf{x}_t+\mathbf{u}^{c^d}\mathbf{d}_{t-1}+b^{c^d})\)是GRU中的更新门。
Offline Model Training
和传统VAE类似,模型的训练可以通过优化ELBO来完成。记长度为\(T+1\)的输入序列为\(\mathbf{x}_{t-T:t}\),隐空间变量采样次数为\(L\),第\(l\)个隐空间变量为\(\mathbf{l}^{(l)}_{t-T:t}\),损失函数可以写成如下形式:
\[ \tilde{\mathcal{L}}(\mathbf{x}_{t-T:t})\approx\frac{1}{L}\sum_{t=1}^L[\log(p_\theta(\mathbf{x}_{t-T:t}|\mathbf{z}_{t-T:t}^{(l)}))+\log(p_\theta(\mathbf{z}_{t-T:t}^{(l)}))-\log(q_\phi(\mathbf{z}_{t-T:t}^{(l)}|\mathbf{x}_{t-T:t}))] \]
第一项\(\log(p_\theta(\mathbf{x}_{t-T:t}|\mathbf{z}_{t-T:t}^{(l)}))\)可以看作是重构误差;第二项\(\log(p_\theta(\mathbf{z}_{t-T:t}))=\sum_{i=t-T}^t \log(p_\theta(\mathbf{z}_i|\mathbf{z}_{i-1}))\)通过Linear Gaussian State Space Model计算;第三项\(-\log(q_\phi(\mathbf{z}_{t-T:t}|\mathbf{x}_{t-T:t}))=-\sum_{i=t-T}^t\log(q_\phi(\mathbf{z}_i|\mathbf{z}_{i-1},\mathbf{x}_{t-T:i}))\)为隐变量\(\mathbf{z}\)后验分布的估计,同时\(\mathbf{z}_i\)是经Planar Normalizing Flow转换过的。
Online Detection
在训练好模型之后,就可以进行异常检测了。在时间\(t\),我们通过根据长度为\(T+1\)的序列\(\mathbf{x}_{t-T:t}\)来重构\(\mathbf{x}_t\),并根据重构概率\(\log(p_\theta(\mathbf{x}_t|\mathbf{z}_{t-T:t}))\)来判定异常。定义\(\mathbf{x}_t\)对应的异常分数\(S_t=\log(p_\theta(\mathbf{x}_t|\mathbf{z}_{t-T:t}))\),高异常分数代表样本\(\mathbf{x}_t\)能够以大概率重构(因为模型是用正常样本训练,可以认为模型建模的是正常样本的分布,重构概率高就代表符合正常分布)。给定阈值之后便可根据异常分数来进行异常的判定。
Automatic Threshold Selection
在异常检测阶段,需要根据设定的阈值和每个样本的异常分数来判断该样本是否为异常,所以阈值的选择十分重要。文中用到了一种根据Extreme Value Theory自动选择阈值的算法。对于一个分布,其中的极端事件往往位于分布的末尾,而Extreme Value Theory第一定理给出不管原始分布如何,这些极端事件的分布服从一个带参的分布族。因此,可以在对数据分布未知的情况下估计极端事件的分布。
除了Extreme Value Theory第一定理之外,Extreme Value Theory第二定理给出随机变量大于特定阈值\(t\)的分布可以用Generalized Pareto Distribution来描述。作者使用了基于Extreme Value Theory第二定理的Peaks-Over-Threshold算法来进行阈值的选择。因为Extreme Value Theory第二定理给出随机变量大于特定阈值\(t\)的分布,而在本文的场景中我们需要刻画的异常点的分布应该是小于一个给定阈值的分布,所以需要修改一下公式。
对于给定的数据,模型会给出对应的异常分数序列\(\{S_1,S_2,\cdots,S_{N^\prime}\}\),给定预先设定的阈值\(th\),\(S_i\)极端部分(即小于\(th\)的部分)的分布符合Generalized Pareto Distribution,公式如下: \[ \bar{F}(s)=P(th-S>s|S<th)\sim(1+\frac{\gamma s}{\beta})^{-\frac{1}{\gamma}} \]
其中\(\gamma\)和\(\beta\)为分布的形状参数,本文使用极大似然估计来对参数进行估计。设参数的估计值分别为\(\hat{\gamma}\)和\(\hat{\beta}\),最终的阈值\(th_F\)由拟合得到的分布的分位数确定:
\[ th_F\simeq th-\frac{\hat{\beta}}{\hat{\gamma}}((\frac{qN^\prime}{N^\prime_{th}})^{-\hat{\gamma}}-1) \]
其中\(q\)为期望\(S<th\)的概率,\(N^\prime\)为观测值的数量,\(N^\prime_{th}\)为\(S_i<th\)的个数。
Anomaly Interpretation
\[ \log(p_\theta(\mathbf{x}_t|\mathbf{z}_{t-T:t}))=\sum_{i=1}^M\log(p_\theta(x_t^i|\mathbf{z}_{t-T:t})) \]
Experiments
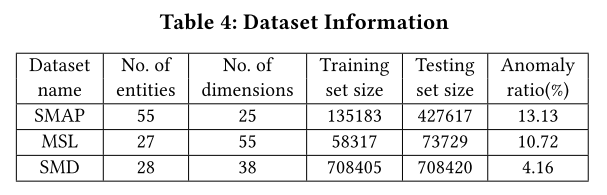
Datasets and Metrics
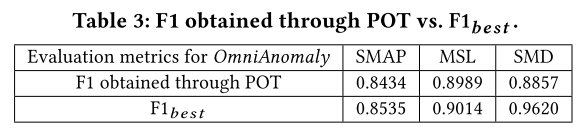
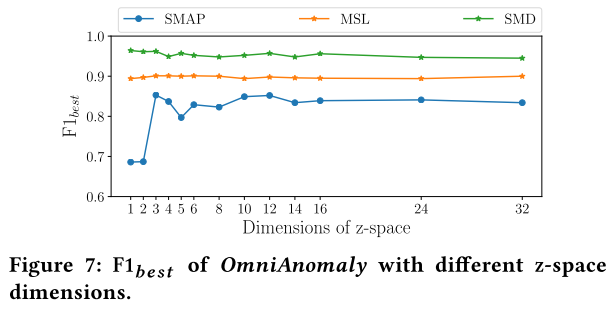
Overall Performance
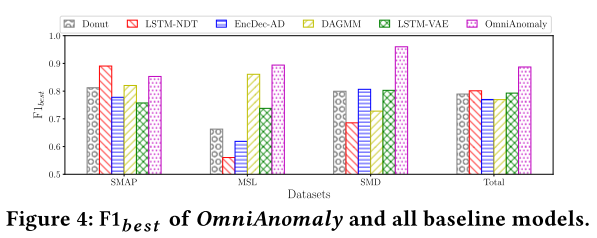

Effects of Major Techniques

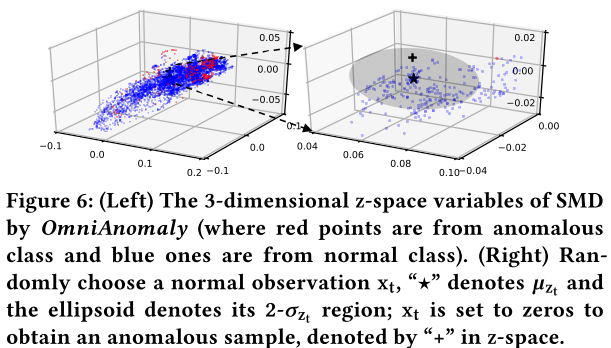
Visualization on Z-Space Representations
本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!