Recurrent Neural Networks for Multivariate Time Series with Missing Values
本文最后更新于:2 年前
Abstract
文中提出了一种可以处理带缺失值多为时间序列的GRU模型:GRU-D。本模型不仅可以捕捉时间序列中的长期依赖模式,并且还能利用时间序列中的缺失模式来达到更好的时间序列预测效果。
Methodology
Notations
记包含\(D\)个变量的多变量时间序列为\(X=(x_1,x_2,\cdots,x_T)^T\in\mathbb{R}^{T\times D}\),其中对于每个\(t\in\{1,2,\cdots,T\},x_t\in\mathbb{R}^D\)表示时间序列在时间\(t\)的观测值,\(x_t^d\)表示\(x_t\)的第\(d\)个成分。记\(s_t\in\mathbb{R}\)为\(t\)时刻的时间戳,并假设第一个观测值的时间戳为\(0\)。对于包含缺失值的时间序列,我们用Masking Vector \(m_t\in\{0,1\}\)进行标记,同时对每个\(x_t^d\)维护距离上一个观测值的Time Interval \(\delta_t^d\in\mathbb{R}\),公式如下: \[ m_t^d=\begin{cases}1, &\text{if }x_t^d\text{ is observed}\\0, &\text{otherwise}\end{cases} \]
\[ \delta_t^d=\begin{cases}s_t-s_{t-1}+\delta_{t-1}^d, &t>1,m_{t-1}^d=0\\s_t-s_{t-1}, &t>1, m_{t-1}^d=1\\0, &t=1\end{cases} \]
下图是一些示例:

在本文中,我们主要关注时间序列的分类问题,即给定数据集\(\mathcal{D}=\{(X_n,s_n,M_n)\}_{n=1}^N\),我们要对每个样本的类别进行预测\(l_n\in\{1,\cdots,L\}\)。
GRU-RNN for Time Series Classification
GRU是一种改进版本的RNN,其最大不同是加入了门控机制。GRU单元的结构如下图所示:
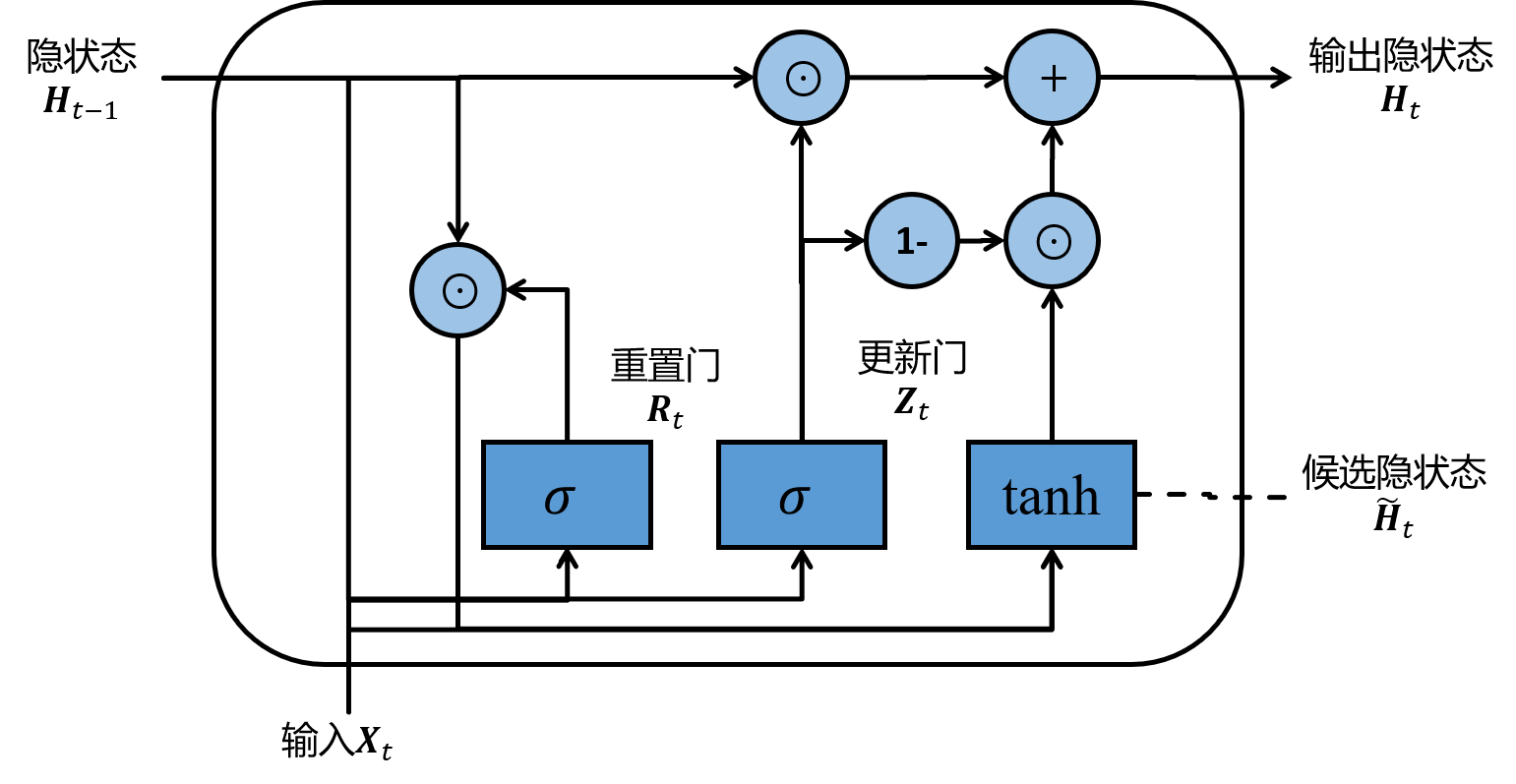
GRU包含了重置门和更新门,其中重置门\(R_t\)负责控制上一时间的隐状态\(h_{t-1}\)有多少部分需要保留,而更新门则决定由\(R_t\)计算出来的候选隐状态\(\tilde{h}_t\)有多少部分需要保留。最后当前时间的隐状态由\(h_{t-1}\)和\(\tilde{h}_t\)共同算出。GRU的状态更新公式如下: \[ \begin{align} R_t&=\sigma(W_rx_t+U_rh_{t-1}+b_r)\\ Z_t&=\sigma(W_zx_t+U_zh_{t-1}+b_z)\\ \tilde{h}_t&=\text{tanh}(Wx_t+U(R_t\odot h_{t-1})+b)\\ h_t&=(1-Z_t)\odot h_{t-1}+Z_t\odot \tilde{h}_t \end{align} \] 文中提出了一些处理缺失值的简单方法:
- 直接用均值替代:\(x_t^d\leftarrow m_t^dx_t^d+(1-m_t^d)\tilde{x}^d\),其中\(\tilde{x}^d=\frac{\sum_{n=1}^N\sum_{t=1}^{T_n}m_{t,n}^d x_{t,n}^d}{\sum_{n=1}^N\sum_{t=1}^{T_n}m_{t,n}^d\tilde{x}^d}\)。这种方法称为GRU-Mean;
- 用上一个观测值替代:\(x_t^d\leftarrow m_t^d x_t^d+(1-m_t^d)x_{t^\prime}^d\)。这种方法称为GRU-Forward;
- 不填充,将是否缺失,距离上一个观测值的时间作为额外信息输入:\(x_t^{(n)}\leftarrow[x_t^{(n)};m_t^{(n)};\delta_t^{(n)}]\)。这种方法称为GRU-Simple。
GRU-D: Model with Trainable Decays
文中提出了时间序列缺失值的两个性质:一个是在上一个观测值距离很远的情况下缺失值倾向于接近一个默认的值,第二个是缺失值的影响会随着时间减弱。为了体现上述两点,文中提出了GPU-D模型,模型框架如下:
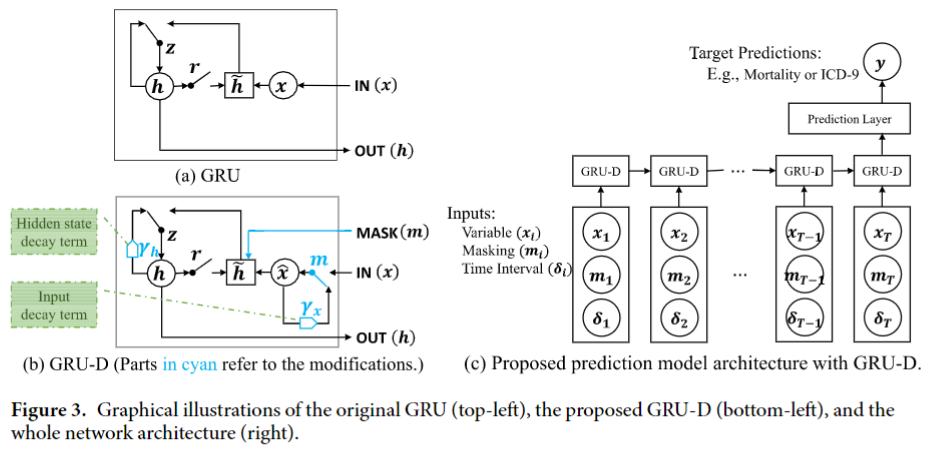
在模型中,Decay Rates被设定为一个带参数的函数和GRU一起训练: \[ \gamma_t=\exp\{-\max(0,W_\gamma\delta_t+b_\gamma)\} \]
\[ \hat{x}_t^d=m_t^dx_t^d+(1-m_t^d)(\gamma_{x_t}^dx_{t^\prime}^d+(1-\gamma_{x_t}^d)\tilde{x}^d) \] 其中\(x_{t^\prime}^d\)是第\(d\)个变量的上一个观测值,\(\tilde{x}^d\)是第\(d\)个变量的经验均值。这样\(\hat{x}_t^d\)就代表经过Input Decay的输入。
文中提到只用Input Decay是不够的,除此之外作者还使用了Hidden State Decay,即对\(h_{t-1}\)进行Decay,公式如下: \[ \hat{h}_{t-1}=\gamma_{h_t}\odot h_{t-1} \] 用Decay之后的\(\hat{x}_t\)和\(\hat{h}_{t-1}\)替换原始的GRU公式就得到了GRU-D模型: \[ \begin{align} R_t&=\sigma(W_r\hat{x}_t-U_r\hat{h}_{t-1}+V_rm_t+b_r)\\ Z_t&=\sigma(W_z\hat{x}_t+U_z\hat{h}_{t-1}+V_zm_t+b_z)\\ \tilde{h}_t&=\text{tanh}(W\hat{x}_t+U(R_t\odot \hat{h}_{t-1})+Vm_t+b)\\ h_t&=(1-z_t)\odot \hat{h}_{t-1}+z_t\odot\tilde{h}_t \end{align} \]
Experiments
Baseline Imputation Methods
下图为文中比较中用到的Baseline:

Baseline Prediction Methods
下图为文中用到的用来预测的Baseline:

Results
文中用到的数据集如下:
- Gesture phase segmentation dataset (Gesture).
- PhysioNet Challenge 2012 dataset (PhysioNet).
- MIMIC-Ⅲ dataset (MIMIC-Ⅲ).
下图展示了不同方法在人工合成数据集上的表现:
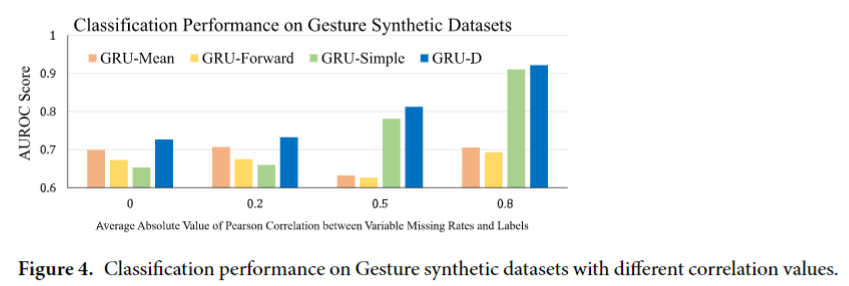
下表展示了不同模型在预测任务表现的对比:
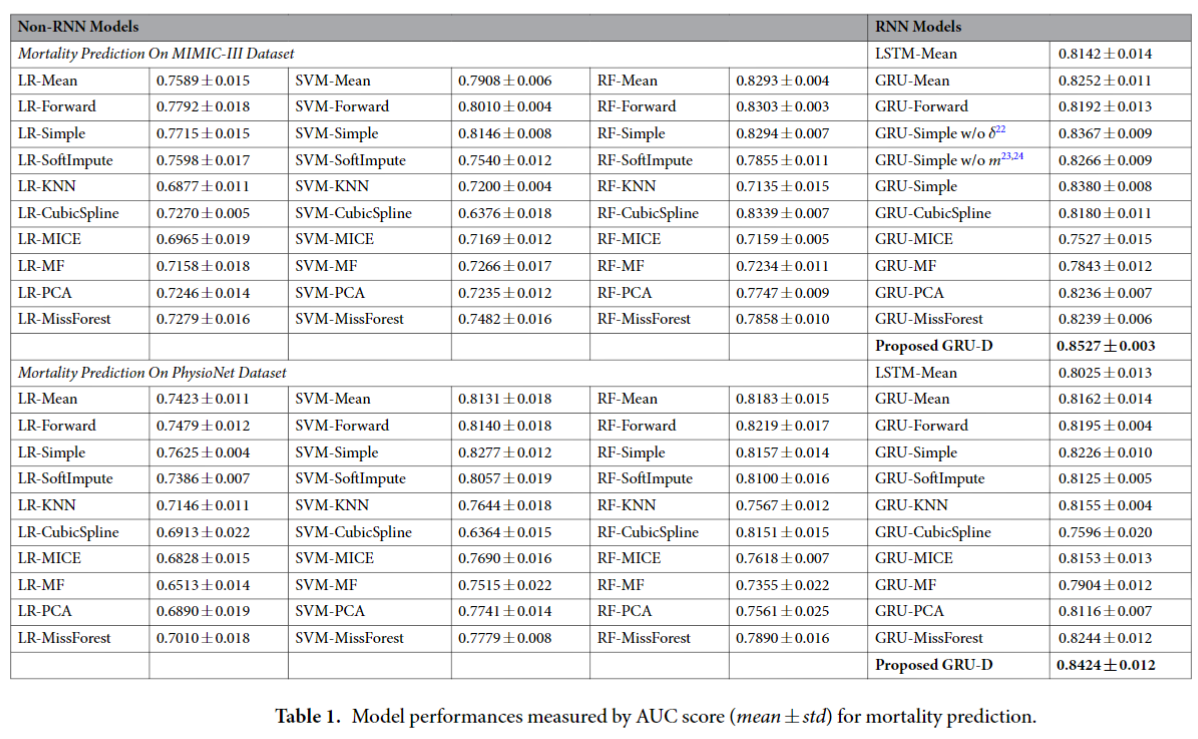
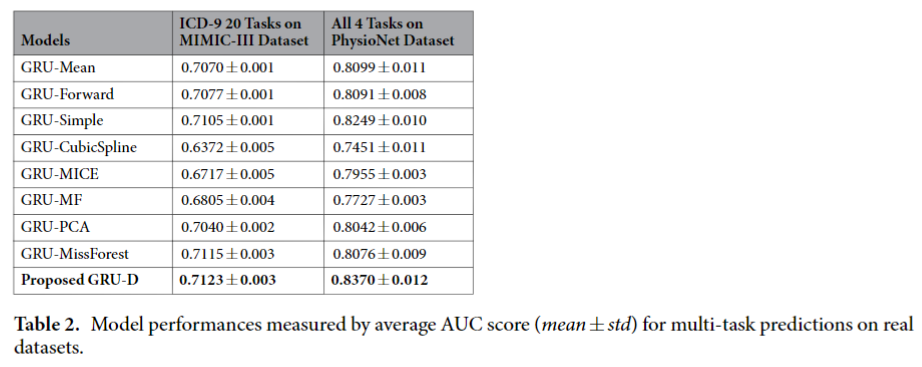
下表展示了不同方法在MIMIC-Ⅲ和PhysioNet数据集上的多任务表现:
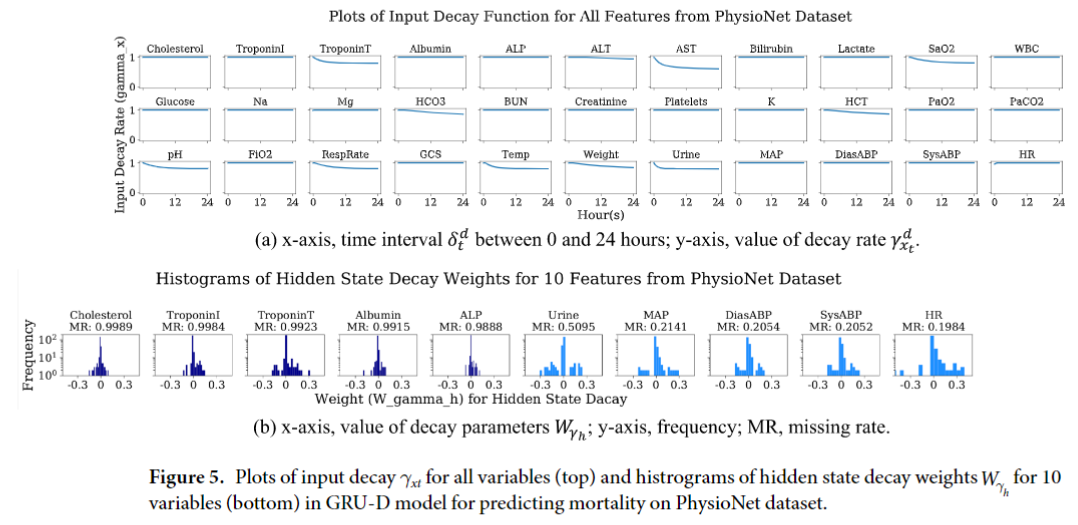
下图分别展示了模型学到的Input Decay和Hidden State Decay:
本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!