GAIN: Missing Data Imputation using Generative Adversarial Nets
本文最后更新于:2 年前
Abstract
本文基于GAN提出了一种时间序列缺失值填充(Time Series Imputation)的方法。其主要的思路为生成器\(G\)从隐空间\(Z\)生成完整的样本,而判别器\(D\)则输出样本中不同部分为真实的概率。除此之外,作者提出了使用Hint Vector来揭示原始数据中缺失部分的信息,来优化训练过程。
Methodology
Problem Formulation
考虑一个\(d\)维的空间\(\mathcal{X}=\mathcal{X}_1\times \cdots\times \mathcal{X}_d\),设\(\mathbf{X}=(X_1,\cdots,X_d)\)维空间\(\mathcal{X}\)上的随机向量(即理想的完整的时间序列),记其分布为\(P(\mathbf{X})\)。设\(\mathbf{M}=(M_1,\cdots,M_d)\)为Mask向量表示\(\mathbf{X}\)中被观察到的部分。(即标识时间序列哪些部分有缺失),取值为\(\{0,1\}^d\)。
对于每一个\(i\in\{1,\cdots,d\}\),我们定义一个新空间\(\tilde{\mathcal{X}}=\mathcal{X}\cup\{*\}\),其中\(*\)表示不属于任意\(\mathcal{X}_i\)的一个点。令\(\tilde{\mathcal{X}}=\tilde{\mathcal{X}_1}\times\cdots\times\tilde{\mathcal{X}_d}\),同时定义一个新的随机变量(即我们观测到的含有缺失值的时间序列)\(\tilde{\mathbf{X}}=(\tilde{X}_1,\cdots,\tilde{X}_d)\in \tilde{\mathcal{X}}\): \[ \tilde{X}_i=\begin{cases}X_i,&\text{if } M_i=1\\*,&\text{otherwise}\end{cases} \] 假设数据集的形式为\(\mathcal{D}=\{(\tilde{x}^i,m^i)\}^n_{i=1}\),我们的任务是从\(P(\mathbf{X}|\tilde{\mathbf{X}}=\tilde{x}^i)\)上采样来对缺失值进行填充。
Model Architecture
模型的架构如下图所示:
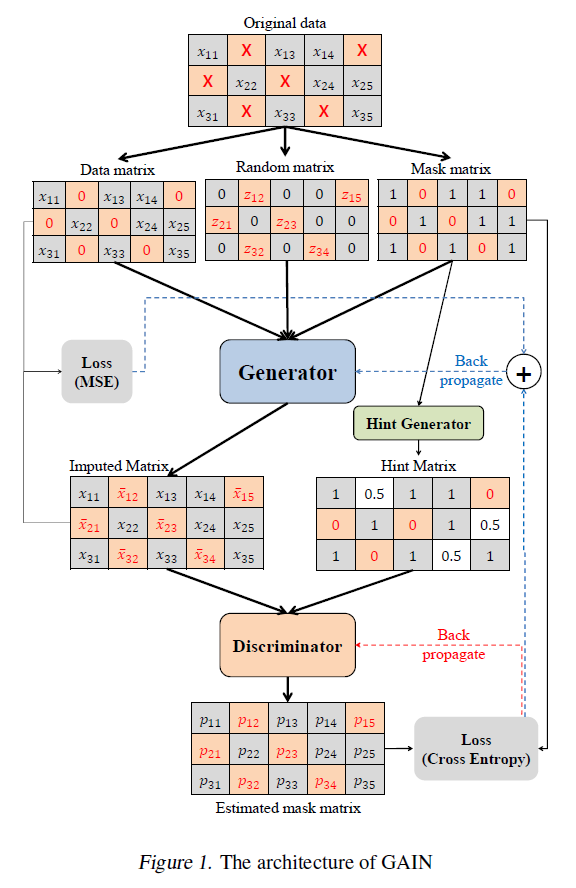
Generator
生成器的输入有三项:\(\tilde{\mathbf{X}}\),\(\mathbf{M}\)和随机噪声\(\mathbf{Z}\),输出设为\(\bar{\mathbf{X}}\)。设生成器为映射\(G: \tilde{\mathcal{X}}\times\{0,1\}^d\times[0,1]^d\rightarrow \mathcal{X}\),而\(\mathbf{Z}\)为\(d\)维的高斯噪声。生成器的输出和填充后的时间序列定义为: \[ \begin{align} \bar{\mathbf{X}}&=G(\tilde{\mathbf{X}},\mathbf{M},(1-\mathbf{M})\odot\mathbf{Z})\\ \hat{\mathbf{X}}&=\mathbf{M}\odot\tilde{\mathbf{X}}+(1-\mathbf{M})\odot\bar{\mathbf{X}} \end{align} \] \(\bar{\mathbf{X}}\)即为生成器的直接输出,因为其实有些部分没有缺失,生成器还是会为每个部分输出值。
\(\hat{\mathbf{X}}\)为填充后的时间序列,对于缺失的部分采用生成器的输出进行填充。
Discriminator
和原始的GAN不同的是,我们不需要判断整个样本是真实的或者是生成的,而是需要判断样本的那些部分是真实的或者是生成的,所以判别器为映射\(D: \mathcal{X}\rightarrow[0,1]^d\)。判别器的具体目标函数将在后面讨论。
Hint
Hint是一种提示机值,是一个和\(\mathbf{X}\)相同维度的随机变量\(\mathbf{H}\),其分布依赖于\(\mathbf{M}\)。\(\mathbf{H}\)是由用户自己定义的,相当于一种不完整的\(\mathbf{M}\),用来作为判别器的额外输入。
Objective
我们训练判别器最大化正确预测\(\mathbf{M}\)的概率,而生成器最小化判别器正确预测\(\mathbf{M}\)的概率,目标函数如下: \[ \begin{align} V(D,G)=&\mathbb{E}_{\hat{X},M,H}[\mathbf{M}^T\log D(\hat{\mathbf{X}},\mathbf{H})\\&+(1-\mathbf{M})^T\log(1-D(\hat{\mathbf{X}},\mathbf{H}))] \end{align} \] 按照标准的GAN可以将优化函数写成以下的形式: \[ \min_G\max_D V(D,G) \] 在这里判别器的任务可以看作是一个二分类,而目标函数就是二值交叉熵的定义,因此可以写为: \[ \mathcal{L}(a,b)=\sum\limits_{i=1}^d[a_i\log(b_i)+(1-a_i)\log(1-b_i)] \] \(\mathbf{M}\)可以看作Ground Truth,记\(\hat{\mathbf{M}}=D(\hat{\mathbf{X},\mathbf{H}})\),即判别器输出的预测,因此优化函数可以简记为: \[ \min_G\max_D\mathbb{E}[\mathcal{L}(\mathbf{M},\hat{\mathbf{M}})] \]
GAIN Algorithm
下面讨论GAIN算法的训练流程。
本文通过理论讨论,给出了生成Hint Vector的一个方法,首先定义随机变量\(\mathbf{B}=(B_1,\cdots,B_d)\in\{0,1\}^d\),\(\mathbf{B}\)通过从\(\{1,\cdots,d\}\)随机均匀采样一个\(k\),然后由下列公式得到: \[ B_j=\begin{cases}1, &\text{if }j\neq k\\0, &\text{if }j=k\end{cases} \] 定义空间\(\mathcal{H}=\{0,0.5,1\}^d\),Hint Vector为\(\mathbf{H}=\mathbf{B}\odot\mathbf{M}+0.5(1-\mathbf{B})\in\mathcal{H}\)。
判别器的训练过程如下:固定生成器\(G\),对一个大小为\(k_D\)的mini-batch,独立同分布采样\(k_D\)个\(z\)和\(b\),用来计算\(\mathbf{Z}\)和\(\mathbf{B}\)。判别器的损失函数定义如下: \[ \mathcal{L}_D(m,\hat{m},b)=\sum\limits_{i:b_i=0}[m_i\log(\hat{m}_i)+(1-m_i)\log(1-\hat{m}_i)] \] 判别器的优化函数为: \[ \min_D-\sum\limits_{j=1}^{k_D}\mathcal{L}_D(m(j),\hat{m}(j),b(j)) \] 其中\(\hat{m}(j)=D(\hat{x}(j),m(j))\)。
在优化了判别器之后,需要优化生成器,对一个大小为\(k_G\)的mini-batch,生成器的损失函数包含两个部分,一个是在缺失部分的损失:
\[ \mathcal{L}_G(m,\hat{m},b)=-\sum\limits_{i:b_i=0}(1-m_i)\log(\hat{m}_i) \] 一个是未缺失部分的损失: \[ \mathcal{L}_M(x,x^\prime)=\sum\limits_{i=1}^d m_iL_M(x_i,x_i^\prime) \] 其中: \[ L_M(x_i,x_i^\prime)=\begin{cases}(x_i^\prime-x_i)^2, &\text{if }x_i\text{ is continuours},\\-x_i\log(x_i^\prime), &\text{if }x_i\text{ is binary}.\end{cases} \] 最终的优化函数为: \[ \min_G\sum\limits_{j=1}^{k_G}\mathcal{L}_G(m(j),\hat{m}(j),b(j))+\alpha\mathcal{L}_M(\tilde{x}(j),\hat{x}(j)) \] 算法流程如下:

Experiments
下表为在5个不同数据集上实验,与其他5种方法对比的结果:
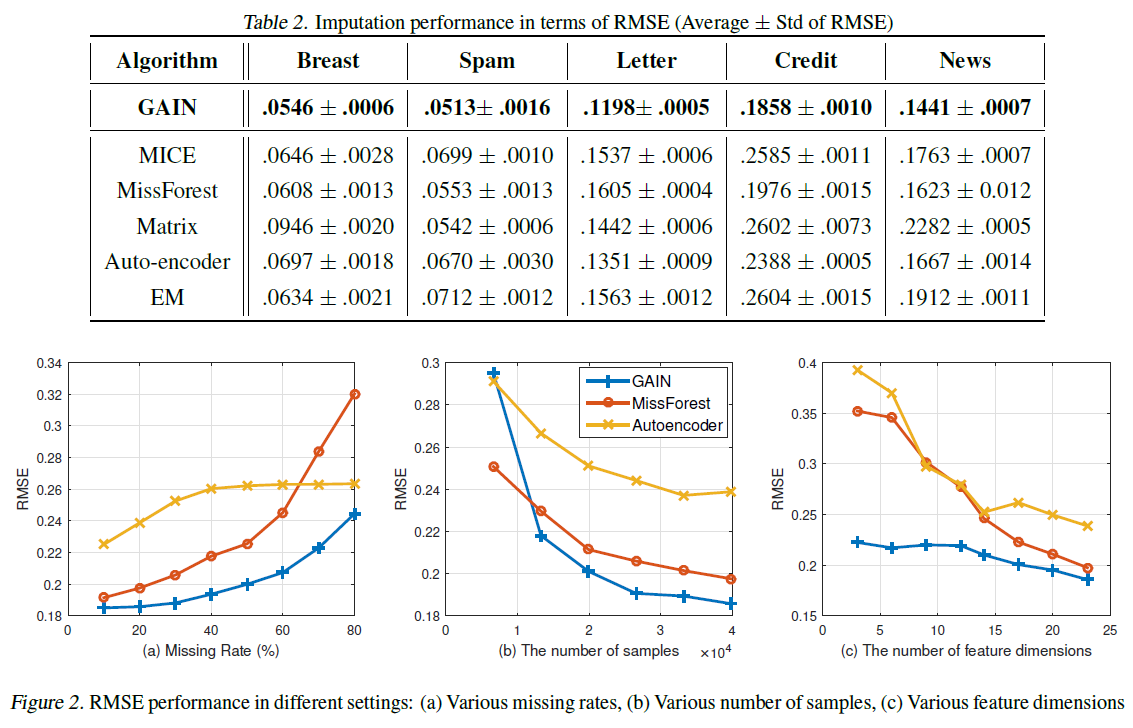
上图为GAIN、MissForest和Autoencoder三种模型在不同缺失比例、样本数量、特征维度下的对比曲线图。
下表为使用不同模型对时间序列进行填充之后,使用逻辑回归进行回归任务的性能:
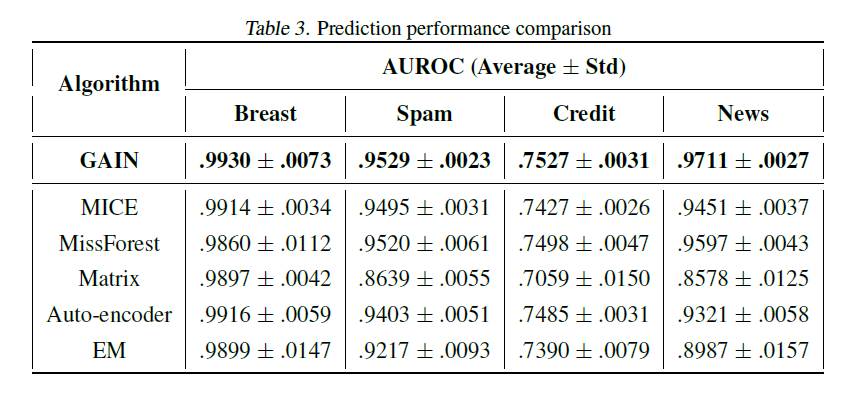
下图为GAIN、MissForest和Autoencoder三种模型在不同缺失比例下的AUROC曲线图:
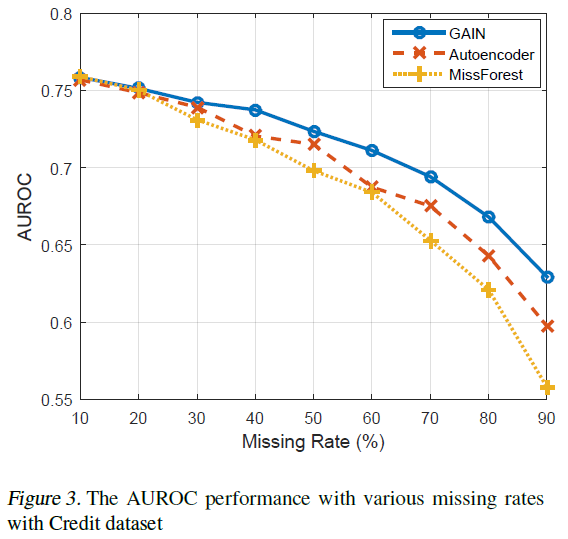
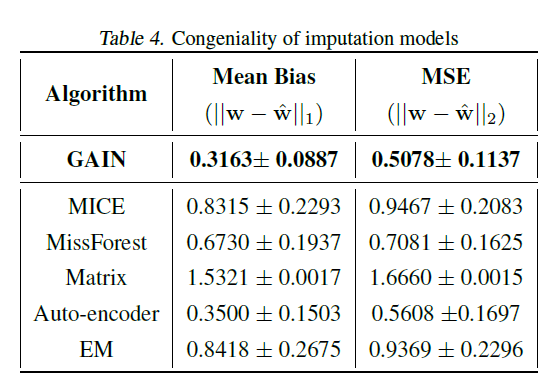
下表展示的是作者对时间序列填充算法保持特征-标签关系的能力。作者分别用完整的数据和填充后的数据用逻辑回归模型进行训练,将两者的权重求绝对值和均方根的结果。
本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!