Unsupervised Anomaly Detection via Variational Auto-Encoder for Seasonal KPIs in Web Applications
本文最后更新于:2 年前
Abstract
本文提出了Donut,一个基于VAE的无监督时间序列异常检测系统。
Contribution
- Donut中使用到了三个技巧,包括改进后的ELBO、缺失数据注入和MCMC插值;
- 提出基于VAE的异常检测训练既需要正常样本也需要异常样本;
- 对Donut提出了在z-空间中基于KDE的理论解释。
Background
Anomaly Detection
对于任意时间\(t\),给定历史观察值\(x_{t-T+1},\cdots,x_t\),确定异常是否发生(记为\(y_t=1\))。通常来收异常检测算法给出的是发生异常的可能性,如\(p(y_t=1|x_{t-T+1},\cdots,x_t)\)。
Methodology
Problem Statement
本文的目的是基于深度生成网络开发具有理论解释性的无监督异常检测算法,并且在有标签的情况下能利用标签信息提升性能。本文基于VAE来构建模型。
Network Structure
算法的总体框架如下图所示:
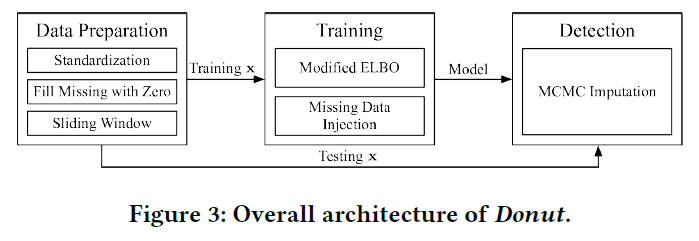
一共包含了预处理、训练和检测三个部分。
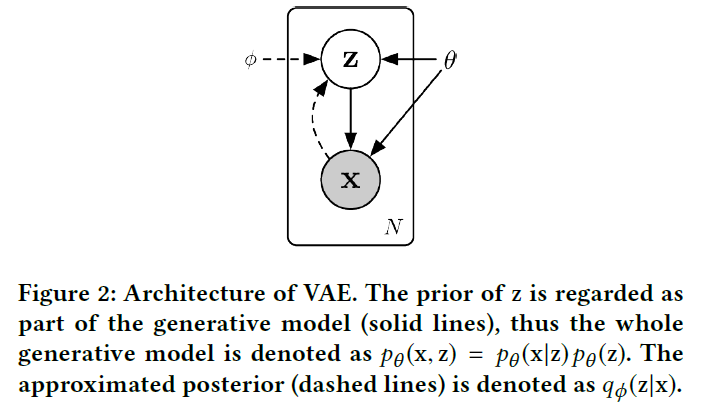
下图为模型的概率图模型:
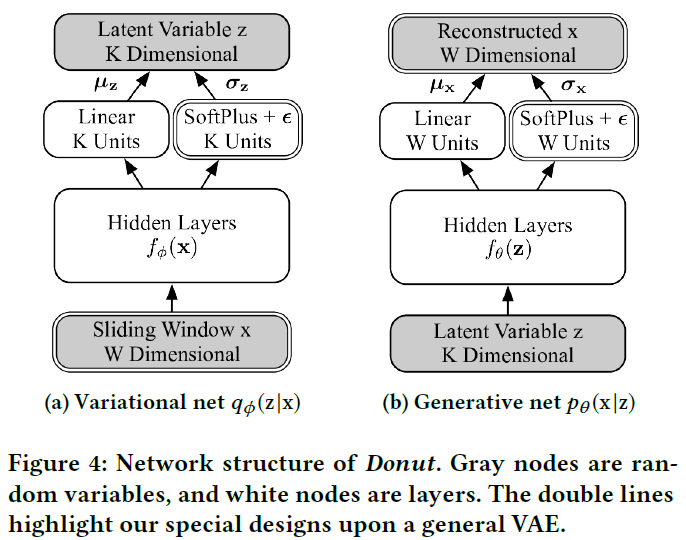
图中双实线的框为本文模型有别于传统VAE的地方,其余地方和VAE一样。先验概率\(p_\theta(z)\)选为标准正态分布\(\mathcal{N}(0,I)\),后验概率\(x\)和\(z\)都是对角化高斯分布,即\(p_\theta(x|z)=\mathcal{N}(\mu_x,\sigma_x^2 I),q_\phi(z|x)=\mathcal{N}(\mu_z,\sigma_z^2 I)\)。如Figure 4所示,推断网络和生成网络中分别都有隐含层\(f_\phi(x)\)和\(f_\theta(z)\)对网络的输入进行特征抽取。高斯分布的参数即从这些抽取出来的特征上得到。均值通过线性层得到:\(\mu_x=W^T_{\mu_x}f_\theta(z)+b_{\mu_x}, \mu_z=W^T_{\mu_z}f_\theta(x)+b_{\mu_z}\)。标准差通过Soft Plus层加一个高斯噪声得到:\(\sigma_x=\text{SoftPlus}[W^T_{\sigma_x}f_\theta(z)+b_{\sigma_x}]+\varepsilon,\sigma_x=\text{SoftPlus}[W^T_{\sigma_z}f_\theta(x)+b_{\sigma_z}]+\varepsilon\)。
文中提到因为KPI的局部方差非常小,所以采用直接建模\(\sigma_x,\sigma_z\)的方式而不是采用对数。除此之外,为了理论上的解释性,文中的神经网络只使用了全连接层。
Training
训练可以直接采用经典的SGVB来优化ELBO: \[ \begin{align} \log p_\theta(x)&\geq\log p_\theta(x)-\text{KL}[q_\phi(z|x)\parallel p_\theta(z|x)]\\ &=\mathcal{L}\\ &=\mathbb{E}_{q_\phi(z|x)}[\log p_\theta(x)+\log p_\theta(z|x)-\log q_\phi(z|x)]\\ &=\mathbb{E}_{q_\phi(z|x)}[\log p_\theta(x,z)-\log q_\phi(z|x)]\\ &=\mathbb{E}_{q_\phi(z|x)}[\log p_\theta(x|z)+\log p_\theta(z)-\log q_\phi(z|x)] \end{align} \] 但是在实际的训练过程中,训练数据需要保证都是正常样本,但实际上训练样本有可能会包含异常或者是缺失值。一种做法是用缺失值填充的算法来填充这些异常值和缺失值,但作者认为使用缺失值填充算法并不能很好的还原数据的正常模式,从而保证算法的有效性。在文中作者采用了修改ELBO的方法,并将其称之为Modified ELBO (M-ELBO),公式如下: \[ \tilde{\mathcal{L}}=\mathbb{E}_{q_\phi(z|x)}[\sum\limits_{w=1}^W{\alpha_w\log p_\theta(x_w|z)+\beta\log p_\theta(z)-\log q_\phi(z|x)}] \] 其中\(\alpha_w\)为指示标记,\(\alpha_w=1\)代表不是异常也不是缺失。\(\beta\)定义为\(\beta=\frac{\sum_{w=1}^W\alpha_w}{W}\)。
在M-ELBO中,异常或缺失值对应的\(\log p_\theta(x_w|z)\)的贡献会被排除,同时\(\log p_\theta(z)\)在乘以\(\beta\)后会相应缩小。作者没有修改\(\log q_\phi(z|x)\)这一项的原因有二:一是\(q_\phi(z|x)\)仅仅是从\(x\)到\(z\)的映射,并不需要考虑“正常模式”;二是\(\mathbb{E}_{q_\phi(z|x)}[-\log q_\phi(z|x)]\)就是\(q_\phi(z|x)\)的熵,而这个在后面的理论分析中有特别的含义。
除此之外还有一种解决方法就是把所有包含异常值和缺失值的窗口去除,这种方法的性能在实验中会进行讨论。
在文中作者还使用了一种Missing Data Injection技术,即在每个Epoch随机的按照一个预设比例\(\lambda\)将正常的数据设为缺失。作者认为这样有助于性能的提升。
Detection
在检测阶段,对于一个输入样本,我们需要模型输出其异常的概率。因为我们建模了\(p_\theta(x|z)\),一种方法是采样计算\(p_\theta(x)=\mathbb{E}_{p_\theta(z)}[p_\theta(x|z)]\),但这种方法计算代价十分昂贵。其他的一些方案有计算\(\mathbb{E}_{q_\phi(z|x)}[p_\theta(x|z)]\)或\(\mathbb{E}_{q_\phi(z|x)}[\log p_\theta(x|z)]\),其中后者被称为"Reconstruction Probability",作者便采用了这种方案。
同时,作者认为输入的检测样本的缺失值会对结果造成较大偏差,于是使用了一种MCMC-based Missing Data Imputation的方法来对检测样本的缺失值进行填充。具体做法是将测试样本分为已观测和缺失两部分\(x=(x_o,x_m)\),然后使用训练好的VAE进行重构得到\((x^\prime_o,x^\prime_m)\),然后用\(x^\prime_m\)替换\(x_m\),这样不断循环如下图所示:
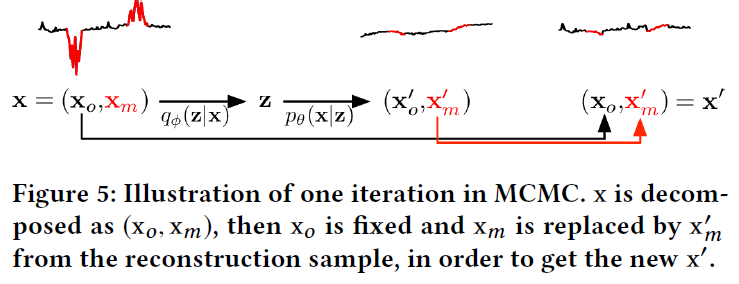
作者使用了\(L\)个样本来计算Reconstruction Probability,虽然得到的输出是针对整个窗口每个点的,但作者只使用最后一个点。
Experiments
Datasets
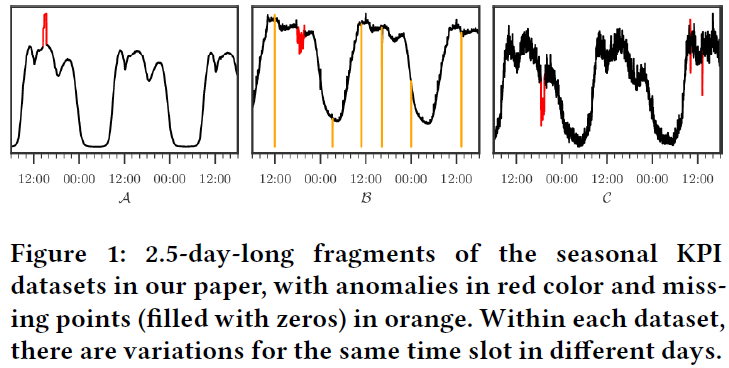
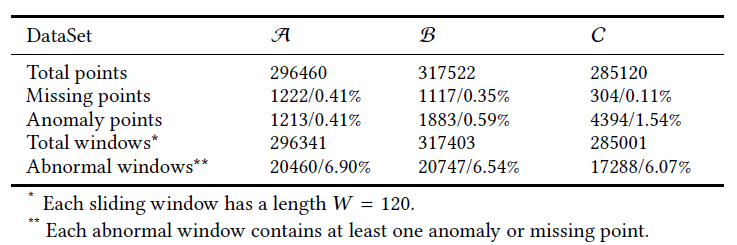
作者选择了三条KPI作为测试数据,分别记为\(\mathcal{A}\),\(\mathcal{B}\),\(\mathcal{C}\),其基本数据如下表所示:
Metrics
因为异常检测类别的极不均衡性,传统的性能指标并不太合适(异常样本极少,且异常一般呈连续的片段)。作者认为在实际应用场景中运维人员需要尽量早的获知异常的发生,于是提出了新的评测机制。

如上图所示,第一行为真实的标签,第二行为预测的异常概率,第三行为预测的标签。第一行中异常片段被加粗表示,对于每一个异常片段的第一个位置\({y}_{t^\prime}\),如果预测的标签中存在\(\hat{y}_{t}\)满足\(t^\prime<t\)且\(|t-t^\prime|\)小于等于预设的阈值\(T\),那么\(y_{t^\prime}\)对应的整段异常都被认为正确检测,否则整段异常都认为没有被正确检测。然后在此基础上计算F1-score,AUC等指标作为评测手段。
Results
Overall Performance
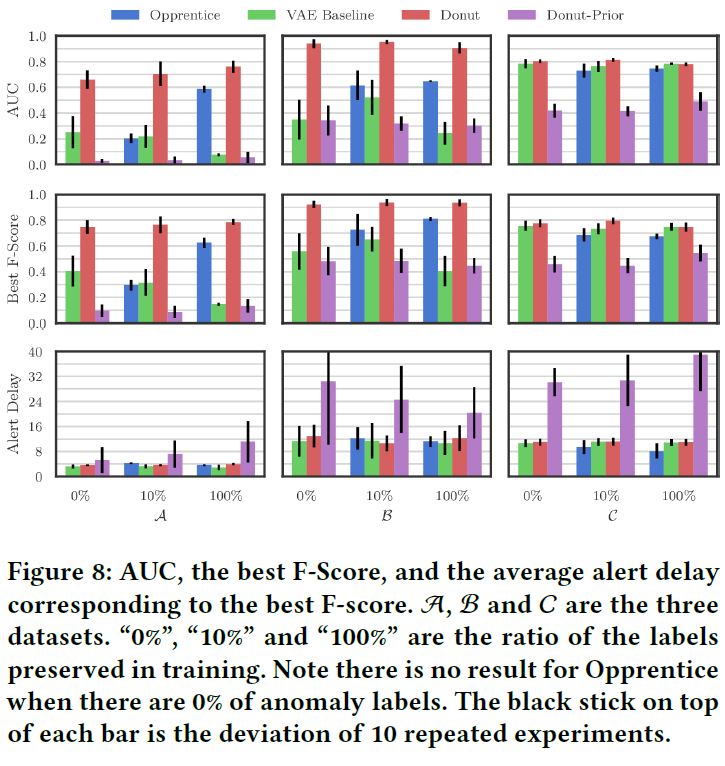
下图展示了不同方法在不同数据集上的表现:
Effects of Donut Techniques
为了探究Donut中所做的各种改进的实际作用,作者做了大量对比实验,结果如下图所示:
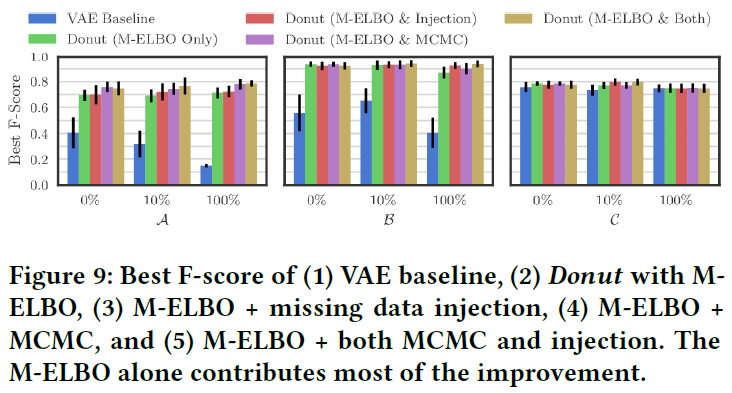
- M-ELBO 从图中可以看出M-ELBO对性能提升最大。作者在文中提到一开始并没期望M-ELBO能带来性能的提升,只是希望它能够Work。这表明在VAE的训练中,只使用正常样本是不够的,也需要加入非正常的信息;
- Missing Data Injection 该技巧的主要作用是增强M-ELBO的效果。从结果上来看作用并不是十分的显著,只是在一些情况下获得了少量的提升;
- MCMC Imputation 作者认为虽然该技巧只在一部分情况下显著提升了性能,但总体来说值得使用。
Impact of K
该部分作者探究了隐变量\(z\)的维度\(K\)对性能的影响,结果如下图:
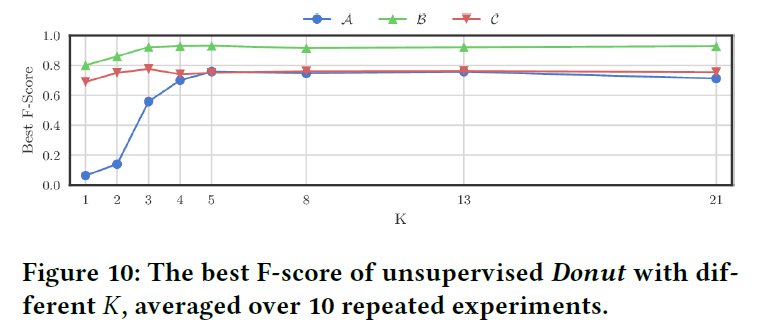
从图上来看,对数据集\(\mathcal{A}\),\(\mathcal{B}\),\(\mathcal{C}\)最佳的\(K\)分别是\(5\),\(4\)和\(3\),但是设定较大的\(K\)并不会对性能有严重的损害。作者还发现对于较为平滑的KPI需要较大的\(K\)。
Analysis
KDE Interpretation
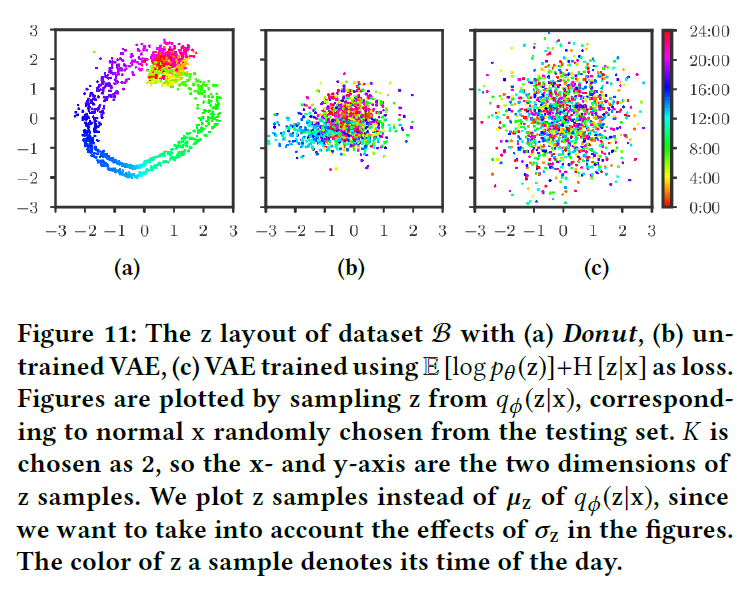
在这一节作者对Reconstruction Probability的意义进行了深入的探讨。首先作者对\(q_\phi(z|x)\)进行了可视化,在图中作者将时间维度用颜色来表示。如Figure 11(a) 所示,\(z\)几乎是按照\(x\)对应的时间呈一个连续的流形分布,作者将这种现象称为Time Gradient。即使Donut没有显式的用到时间信息,不过因为实验用到的数据基本是平滑的,所以说相邻的\(x\)会比较相似,因此经过映射后的\(z\)也会比较相似。作者据此提出Donut的一个优势便是对于没有见过的后验分布\(q_\phi(z|x)\),只要其位于训练过的两个后验之间,也会产生合理的分布。
对于异常的样本\(x\),假设其对应的正常模式为\(\tilde{x}\),作者认为\(q_\phi(z|x)\)会在某种程度上对正常的\(q_\phi(z|\tilde{x})\)进行近似。因为模型是用正常样本进行训练的,隐变量\(z\)的维度通常来说小于样本\(x\),这就导致\(z\)只会保留一部分主要的信息。对于异常样本,其异常模式在编码时就被丢掉了。作者还指出如果\(x\)包含的异常太多,那么模型将难以对\(x\)进行还原。
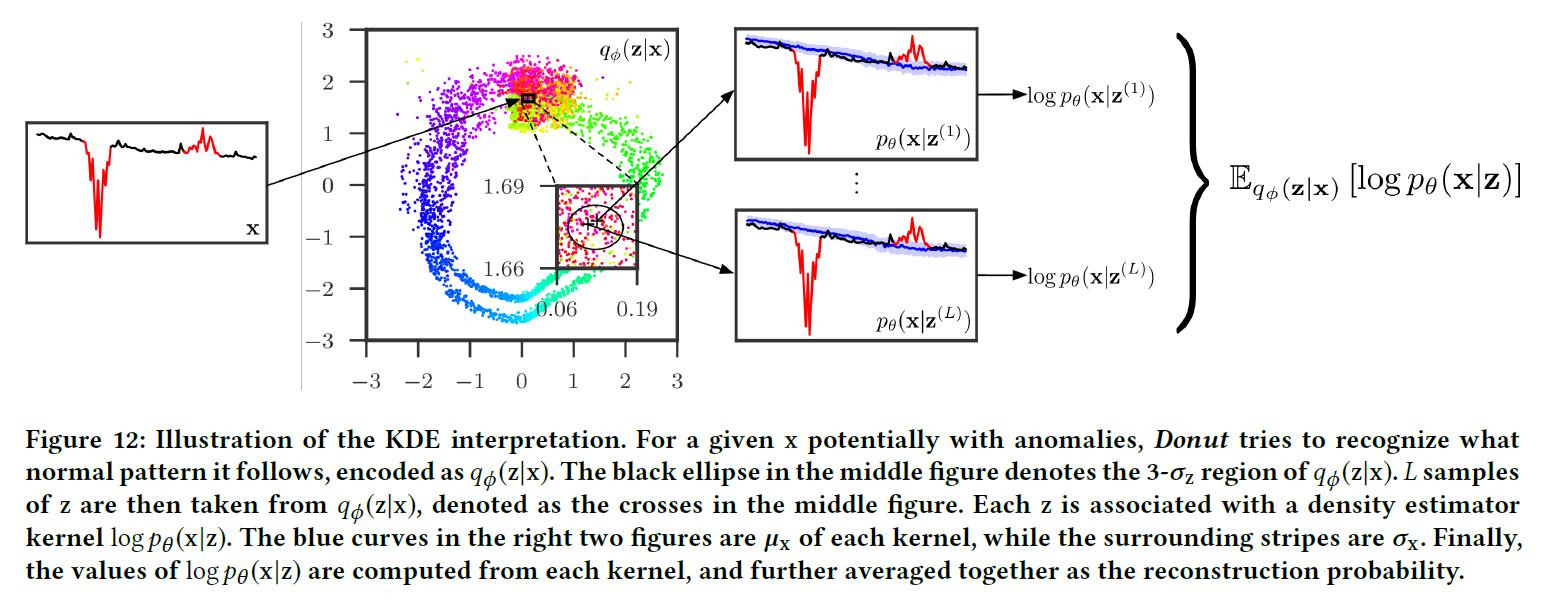
基于上述讨论,作者对使用\(\mathbb{E}_{q_\phi(z|x)}[\log p_\theta(x|z)]\)作为Reconstruction Probability的意义进行了阐释。设输入样本为\(x\),如果其包含异常,假设其对应的正常样本为\(\tilde{x}\),那么\(q_\phi(z|x)\)部分地和\(q_\phi(z|\tilde{x})\)相似。如果\(x\)和\(\tilde{x}\)相似程度高,那么\(\log p_\theta(x|z)\)就会很大(其中\(z\sim q_\phi(z|\tilde{x})\))。\(\log p_\theta(x|z)\)类似于一个密度估计器,代表\(x\)在多大程度上与\(\tilde{x}\)接近,\(\mathbb{E}_{q_\phi(z|x)}[\log p_\theta(x|z)]\)相当于对每一个\(z\)对应的\(\log p_\theta(x|z)\)乘以一个权重\(q_\phi(z|x)\)然后相加。于是作者提出了Reconstruction Probability的KDE Interpretation:在Donut模型中,Reconstruction Probability \(\mathbb{E}_{q_\phi(z|x)}[\log p_\theta(x|z)]\)可以看作是以\(q_\phi(z|x)\)为权重,\(\log p_\theta(x|z)\)为核的核密度估计 (Kernel Density Estimation)。
三维可视化如下图所示:

作者还对直接计算\(p_\theta(x)=\mathbb{E}_{p_\theta(z)}[p_\theta(x|z)]\)进行了质疑,因为这种方法直接求\(x\)的先验,仅仅考虑了\(x\)的总体模式,而忽略了\(x\)的个体模式。
Find Good Posteriors for Abnormal \(x\)
通过上面的讨论我们知道了Donut通过找到\(x\)的正常后验来估计\(x\)在多大程度上与\(\tilde{x}\)相似,在这一节作者讨论了文中使用的不同技巧对找到\(x\)的后验的作用。对于Missing Data Injection作者认为该技巧增强了M-ELBO的效果。对于MCMC Imputation,作者认为该技巧主要是在检测阶段通过不断迭代提供了更好的后验,如下图所示:
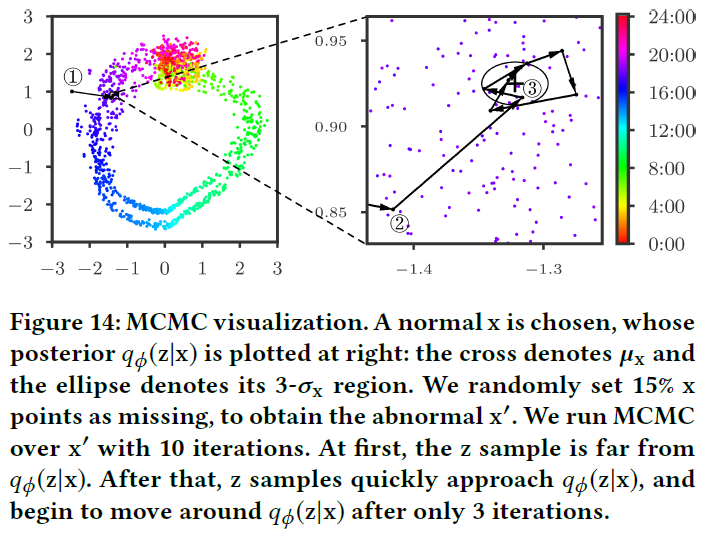
作者认为,虽然对于包含大量异常的样本,Donut不能很好的还原,但在运维场景中,只要对大段异常的开始阶段进行准确预测即可。
Causes of Time Gradient
在这一节作者讨论了Time Gradient出现的原因。首先假设\(x\)都是正常点,这时\(x\)的ELBO为: \[ \begin{align} \mathcal{L}(x)&=\mathbb{E}_{q_\phi(z|x)}[\log p_\theta(x|z)+\log p_\theta(z)-\log q_\phi(z|x)]\\ &=\mathbb{E}[\log p_\theta(x|z)]+\mathbb{E}[\log p_\theta(z)]+\text{H}[z|x] \end{align} \] 第一项表明在\(z\sim q_\phi(z|x)\)下尽可能重构\(x\)。第二项表明\(q_\phi(z|x)\)尽量与\(z\)的先验\(\mathcal{N}(0,I)\)接近。第三项为\(q_\phi(z|x)\)的熵,表明\(q_\phi(z|x)\)应尽量分散。然而第二项又限制了这种分散的区域,如 Figure 11(c) 所示。同时考虑这三项的话,第一项使得\(z\)不能自由地分散,对于不相似的\(x\)其对应的\(z\)也是不相似的,因为要最大化\(x\)的重构概率。然而对于相似的\(x\)来说,其对应的\(q_\phi(z|x)\)会出现很多重复的部分。当达到平衡时,Time Gradient就出现了。
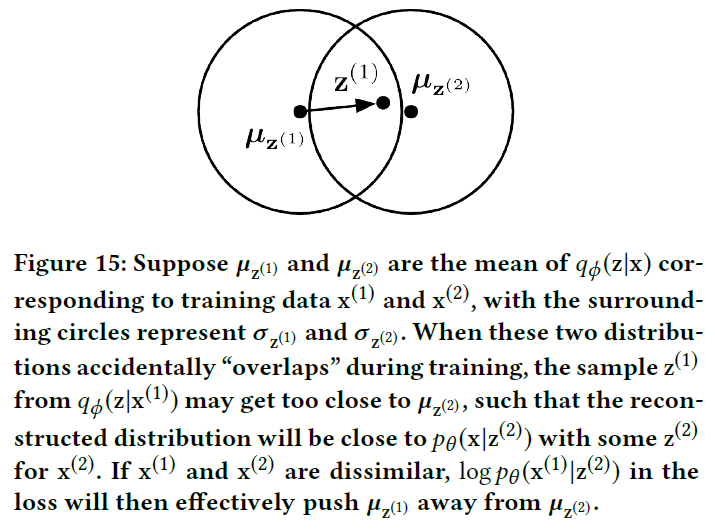
在训练过程中,当\(x\)越不相似,\(q_\phi(z|x)\)就会相距越远,如上图所示。然而在一开始,参数经过随机初始化,\(q_\phi(z|x)\)都是随机散乱的,如 Figure 11(b) 所示。随着训练的进行,\(q_\phi(z|x)\)将会不断优化。由于KPI数据往往是光滑的,那么在时间上相距越远的样本就会越不相似,对应的\(q_\phi(z|x)\)也会相距更远。这也说明了,训练结束后,时间上相距越远的,\(q_\phi(z|x)\)也会相距越远,反之亦然。同时这也表明学习率的设置对本模型的稳定性有至关重要的作用。
Sub-Optimal Equilibrium
上面我们讨论了随着训练进行\(q_\phi(z|x)\)的演变,作者提出在训练过程中可能会遇到模型收敛到次优的情况,如下图所示:
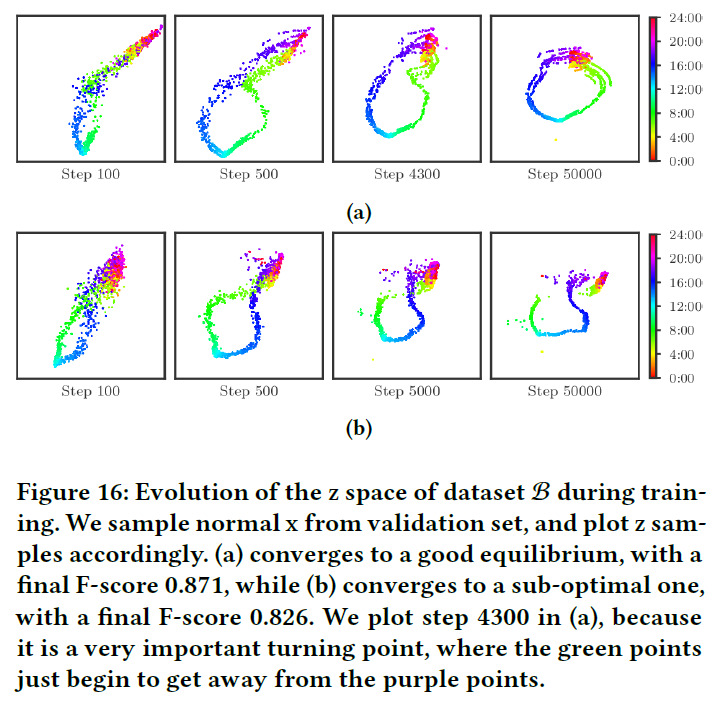
第一行展示的是收敛到最优的情况,第二行展示的是收敛到次优的情况。从第二行的第一个图(Step 100)来看,紫色的点开始穿过绿色的点,随着训练的进行,紫色的点开始将绿色的点推开。到Step 5000的时候,绿色的点已经被分成了两半。下图展示了对应的训练误差和验证误差:
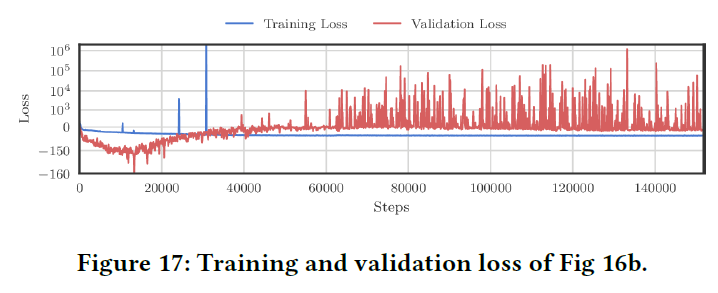
这样的现象会导致在两半绿色区域之间的测试样本会被识别为紫色,从而降低性能。作者提出在\(K\)较大的时候这种现象不容易发生,但这时训练的收敛又会成为一个问题。
本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!