Time-Series Anomaly Detection Service at Microsoft
本文最后更新于:2 年前
Abstract
本文借鉴计算机视觉中的显著性检测,提出了一种基于Spectral Residual的时间序列异常检测算法。
这篇文章还提出了几个时间序列异常检测落地的难点:
- Lack of Labels. 在实际生产环境中会产生大量的KPI,而很难对每个KPI进行人工标注。
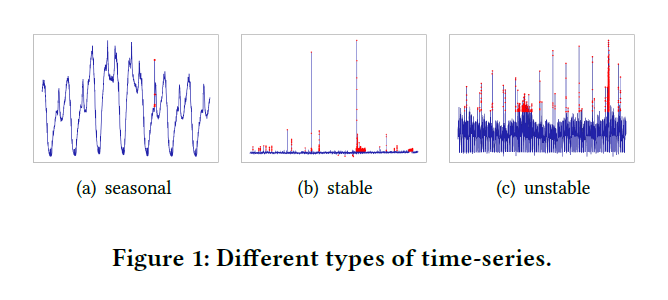
- Generalization. 不同KPI所表现出来的模式也不尽相同,如Figure 1所示。现有方法很难在所有模式的KPI上都表现良好。
- Efficiency. 在实际场景中,会产生大量的时间序列数据,同时对异常检测算法的时间效率有要求。
Contribution
- 将Visual Saliency Detection的方法引入了时间序列异常检测。
- 结合Spectral Residual和CNN提高了异常检测的效果。
- 算法具有良好的时间效率和通用性。
Background
Spectral Residual
SR(Spectral Residual)算法主要包含三个步骤:
- 通过傅里叶变换得到log amplitude spectrum;
- 计算spectral residual;
- 通过傅里叶逆变换回到时间域。
更形式化的表述为如下:
给定一个序列\(\mathbb{x}\),则有:
\[A(f)=Amplitude(\mathscr{F}(\mathbb{x}))\]
\[P(f)=Phrase(\mathscr{F}(\mathbb{x}))\]
\[L(f)=\log(A(f))\]
\[AL(F)=h_1(f)\cdot L(f)\]
\[R(f)=L(f)-AL(f)\]
\[S(\mathbb{x})=\parallel\mathscr{F}^{-1}(\exp(R(f)+iP(f)))\parallel\]
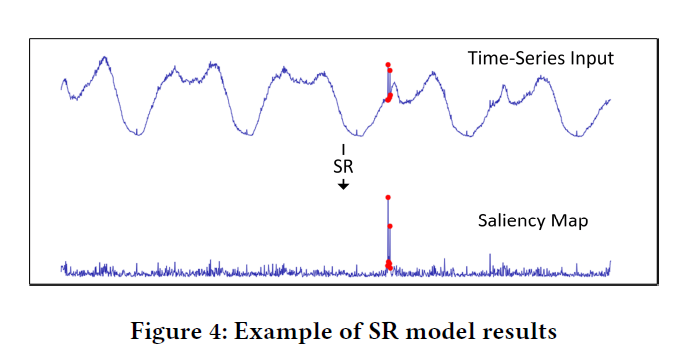
其中\(\mathscr{F}\)和\(\mathscr{F}^{-1}\)分别表示傅里叶变换和傅里叶逆变换;\(\mathbb{x}\in \mathbb{R}^{n\times 1}\)表示输入序列;\(A(f)\)为幅度谱,\(P(f)\)为相位谱,\(L(f)\)为对数幅度谱,\(AL(F)\)为均值滤波后的对数幅度谱;\(R(f)\)为spectral residual;\(S(\mathbb{x})\)称为saliency map。Figure 4为文中给出的Saliency Map示意图。
Methodology
Problem Definition
给定一系列实数值\(\mathbb{x}=x_1,x_2,\cdots,x_n\),时间序列异常检测的任务是产生一个输出序列\(\mathbb{y}=y_1,y_2,\cdots,y_n\)其中\(y_i\in\{0,1\}\)表示\(x_i\)是否为异常点。
SR
对于给定序列\(\mathbb{x}\),计算Saliency Map \(S(\mathbb{x})\),输出序列\(O(\mathbb{x})\)定义为:
\[O(x_i)=\begin{cases}1,\quad \text{if}\frac{S(x_i)-\overline{S(x_i)}}{\overline{S(x_i)}}>\tau\\\\0,\quad \text{otherwise}\end{cases}\]
其中\(S(x_i)\)为\(x_i\)对应的Saliency Map的值,\(\overline{S(x_i)}\)为\(x_i\)附近Saliency Map局部均值。
在实际操作中,FFT是在一个滑动窗口中进行的,文中提到SR方法在点位于窗口中央时效果更好,所以在进行测试的时候,按照如下方法对当前点\(x_n\)(也就是当前序列最后一个点)之后的点进行预测:
\[\overline{g}=\frac{1}{m}\sum_{i=1}^m g(x_n,x_{n-i})\]
\[x_{n+1}=x_{n-m+1}+\overline{g}\cdot m\]
其中\(g(x_i,x_j)\)代表\(x_i\)和\(x_j\)两点构成的直线的梯度;\(\overline{g}\)代表所处理的点的平均梯度;\(m\)为所处理的点的数量。在本文中设置\(m=5\)。文中发现第一个预测的值很重要,所以直接把\(x_{n+1}\)赋值\(k\)次添加到序列的末尾。
SR-CNN
本文提到,仅仅使用一个阈值来进行异常的判断太过简单,于是提出使用一个判别模型来进行异常的判断。由于训练数据没有标签,所以使用如下的公式人工加入异常:
\[x=(\overline{x}+mean)(1+var)\cdot r+x\]
其中\(\overline{x}\)所处理的点的局部均值;\(mean\)和\(var\)为当前滑动窗口点的均值和方差;\(r\sim \mathcal{N}(0,1)\)为服从标准正态分布的噪声。
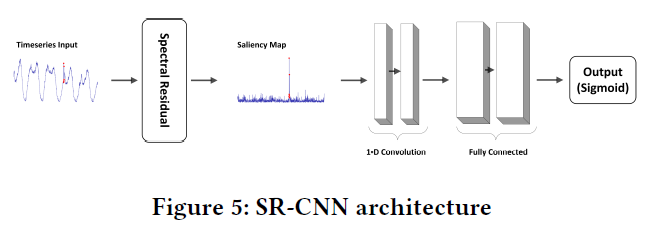
对于判别模型使用的是CNN,主要包含两个1维卷积层(kernel size等于窗口大小\(w\))和两个全连接层。两个卷积层的channel size分别为\(w\)和\(2w\)。
Experiments
Datasets
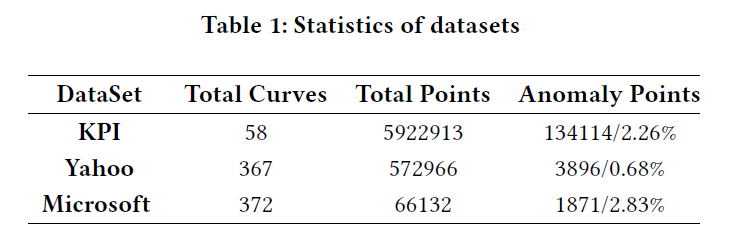
所用数据集包含清华AIOps竞赛数据、Yahoo和Microsoft的KPI数据。
Evaluation Metrics
算法准确率方面用了precision,recall和\(F_1\)-score。

由于在实际场景中KPI的异常往往是以一段一段的形式出现,且并不要求某一个时间点出现异常算法就马上检测出来,只要检测出来的时间在一定的容忍范围内即可。本文使用了一些调整的手段,如Figure 6。对于某一段异常,设段首的异常位于时间点\(t_{truth}\),预测为异常的结果中时间在\(t_{truth}\)之后且距\(t_{truth}\)最近的时间点设为\(t_{predict}\),那么对于一个预先设定的容忍范围\(k\),只要\(t_{predict}-t_{truth}\leq k+1\)那么在预测结果中整段异常就会重置为\(1\),否则全部重置为\(0\)。
Results
实验部分使用了两种训练方式,一种是cold-start,即把所有数据都用来测试,另一种是把数据分为训练测试两部分,在训练集上训练,最后在测试集上进行测试。两种方法适用的baseline不同,最后结果如Table 2和Table 3所示:
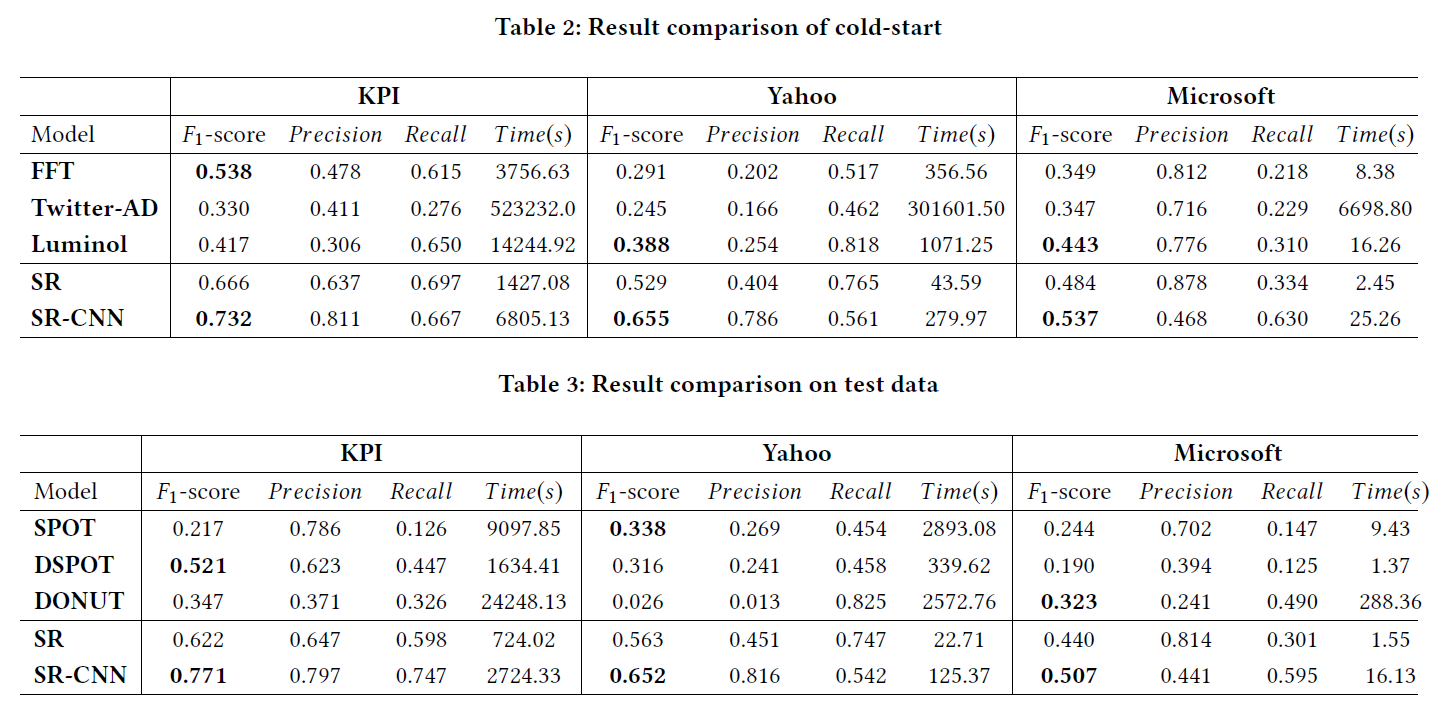
在SR的参数设置上,\(h_q(f)\)中的\(q\)为3,局部平均所用的点数目\(z\)为21,阈值\(\tau\)为3,估计点的数量\(k\)为5,滑动窗口的大小\(w\)在KPI、Yahoo、Microsoft三个数据集上分别为1440、64和30。SR-CNN的\(q\),\(z\),\(k\),\(w\)设置与SR相同。
Additional Experiments with DNN
文中还对有监督的情况进行了测试,具体做法是从时间序列提取特征,然后将Saliency Map也作为特征引入,构造一个有监督的Neural Network进行测试。
提取的特征如Table 5所示:

神经网络的结构为两层全连接层,并添加了Dropout Ratio为0.5的Dropout Layer。两个Layer使用了\(L_1=L_2=0.0001\)的正则化。同时为了处理样本不平衡的情况使用了过采样来使正负样本的比例为\(1:2\)。结构如Figure 7所示:
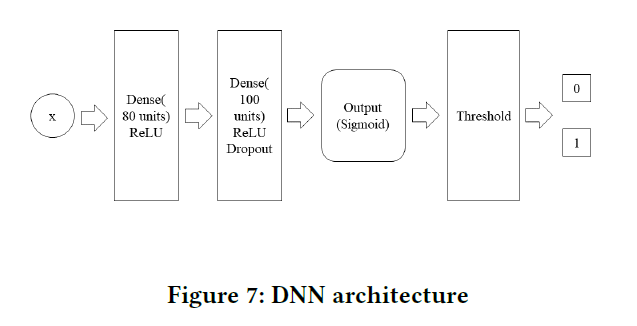
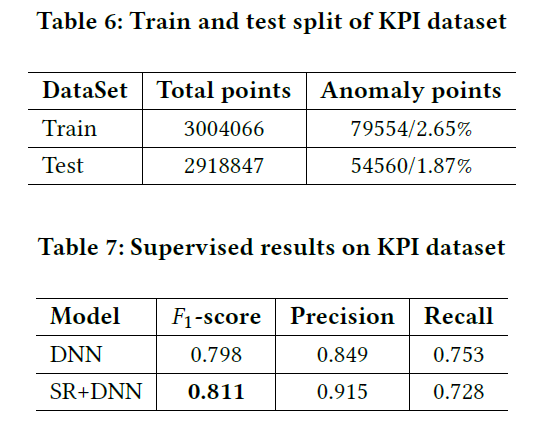
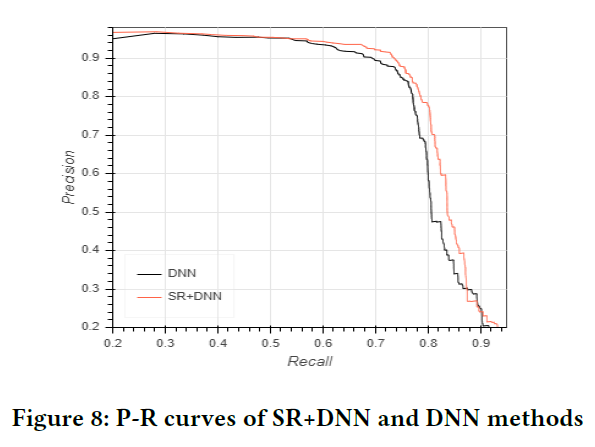
训练测试集的情况如Table 6所示,最终结果如Table 7所示,P-R曲线如Figure 8所示。可以看到使用了SR特征的DNN效果由于没有使用SR特征的DNN。
本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!