Anomaly Detection with Generative Adversarial Networks for Multivariate Time Series

Introduction

这篇文章提出了一个基于GAN的时间序列异常检测模型。

原文

Contribution

1. 提出了基于GAN的时间序列无监督异常检测模型
2. 我们使用基于LSTM的GAN来对多变量时间序列进行建模
3. 结合使用了Residual Loss和Discrimination Loss来进行异常的判断

Background

Generative Adversarial Networks

GANs In a Nutshell, an extremely simple explanation

• 我们想要从一个复杂的、高维的数据分布\(p_r(x)\)上采样得到我们想要的数据点，然而\(p_r(x)\)无法直接求得
• 代替方法：从一个简单的、已知的分布\(p_z(z)\)上采样，然后学习一个Transformation \(G(z): z\rightarrow x\)来将\(z\)映射到\(x\)

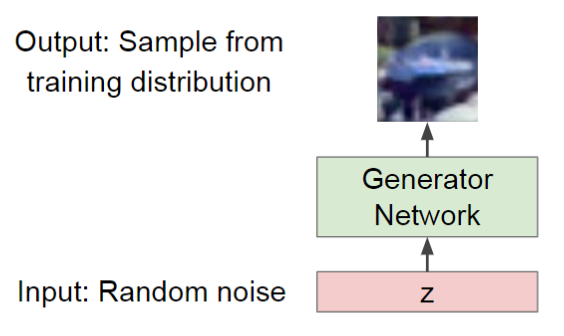
Training: Two-player Game

• Generator Network: 从随机分布\(p_z(z)\)采样\(z\)，通过映射生成样本\(x\)，这个生成的样本要尽量“真实”。怎么“真实”？优化生成器参数\(\theta_G\)最大化判别器对生成样本的评分即可
• Discriminator Network: 接受一个样本\(x\)，判断其是生成的样本还是真实的样本。在训练阶段，我们是知道一个样本\(x\)到底是生成的还是真实的，所以优化判别器参数\(\theta_D\)最小化判别器对生成样本的评分，最大化对真实样本的评分（即最大化分辨真实样本的能力）

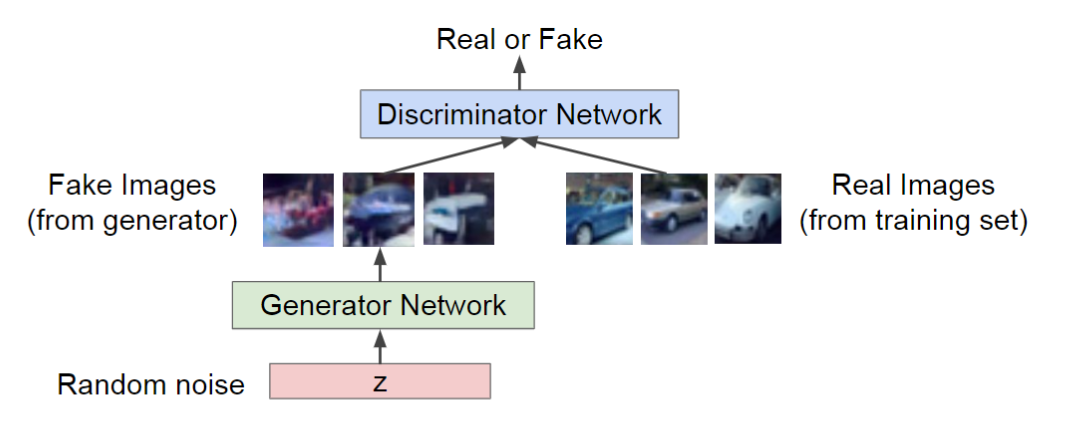
形式化的来讲，优化函数如下：

\[\min\limits_{\theta_G}\max\limits_{\theta_D}V(G,D)=\mathbb{E}_{x\sim p_{data}(x)\log(\underbrace{D_{\theta{D}}(x)}_{判别器对真实样本的评分})}+\mathbb{E}_{z\sim p_z(z)}\log(1-\underbrace{D_{\theta_d}(G_{\theta_G}(z))}_{判别器对生成样本的评分})\]

训练过程如下：

Long Short Time Memory Networks

Vanilla Recurrent Neural Networks

普通的神经网络：

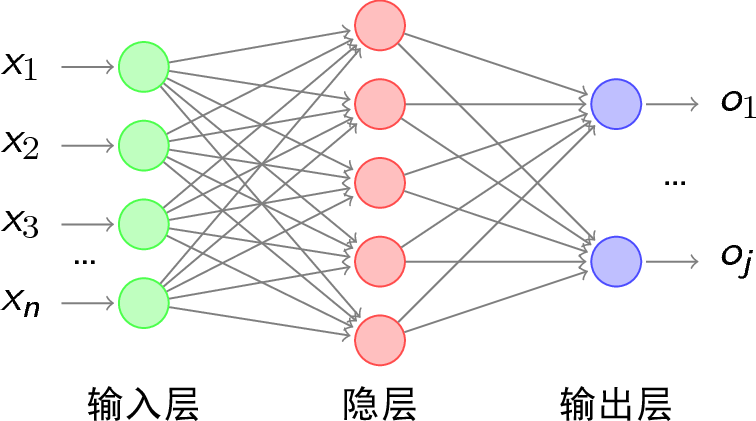
概括的来讲，可以涵盖为一个公式\(\hat{\mathbf{y}}=f(\mathbf{x})\)。对于一个样本\(\mathbf{x}\)，通过多层神经网络映射，输出\(\mathbf{y}\)。

对于RNN，我们处理的是序列数据，也就是说所有样本之间并不是相互独立的。对于一个序列中的一个样本\(x_t\in\{x_1,x_2,\cdots,x_n\}\)，将其输入到神经网络的时候，为了建模\(x_t\)之前的子序列对\(x_t\)的影响关系，需要将这个子序列的信息也输入到神经网络中，怎么做呢？为每一个样本点保存一个State。即定义\(h_t=g(\hat{y_t})=g(f(x_t))\)，对于当前样本点，\(\hat{y_t}=f(x_t,h_{t-1})\)。也就是说神经网络的输入不仅包含了当前样本点的特征，也包含了上一个样本点的“状态”(上一个样本点的“状态”又隐含了上上个样本点的“状态”...)，就像是为网络加上了短期记忆。

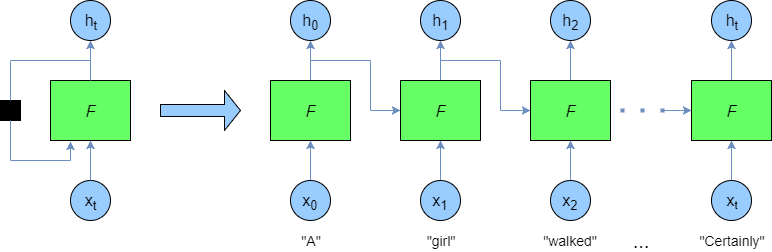
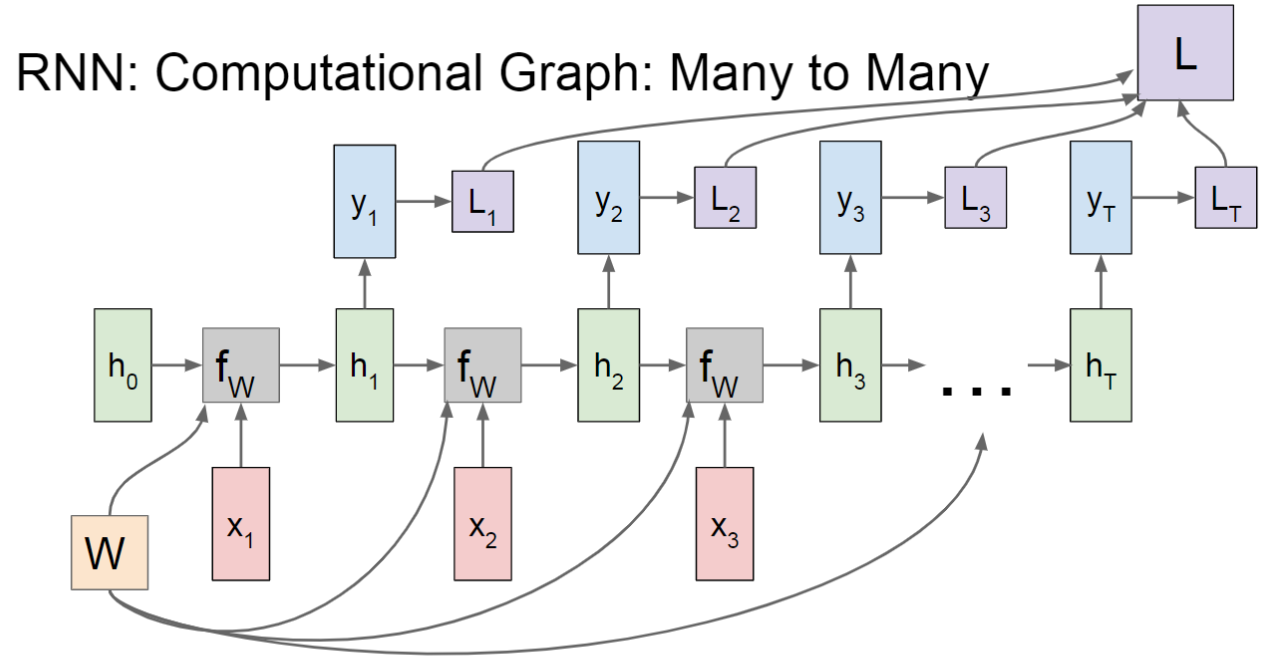
Gradient Flow of Vanilla RNN

下面来进行一些形式化的定义，假设在时刻\(t\)网络输入特征为\(x_t\)，输出隐含状态为\(h_{t}\)，其不仅和当前输入\(x_t\)有关，还和上一个隐含状态\(h_{t-1}\)有关：

• 当前时刻总的净输入\(z_t=Uh_{t-1}+Wx_t+b\)
• 当前时刻输出隐含状态\(h_t=f(z_t)\)
• 当前时刻输出\(\hat{y}_t=Vh_t\)

RNN的梯度更新公式(推导过程比较复杂)：

\[\frac{\partial{\mathcal{L}}}{\partial U}=\sum\limits_{t=1}^T\sum\limits_{k=1}^t \delta_{t,k}\mathbf{h}_{k-1}^T\]

\[\frac{\partial{\mathcal{L}}}{\partial{W}}=\sum\limits_{t=1}^T\sum\limits_{k=1}^t \delta_{t,k}x_k^T\]

\[\frac{\partial\mathcal{L}}{\partial{b}}=\sum\limits_{t=1}^T\sum\limits_{k=1}^t\delta_{t,k}\]

其中\(\delta_{t,k}=\frac{\partial{\mathcal{L}}}{\partial{z_k}}=\text{diag}(f^\prime(z_k))U^T\delta_{t,k+1}\)定义为第\(t\)时刻的损失对第\(k\)时刻隐藏神经层的净输入\(z_k\)的导数，且\(z_k=Uh_{k-1}+Wx_k+b,1\leq k<t\)。

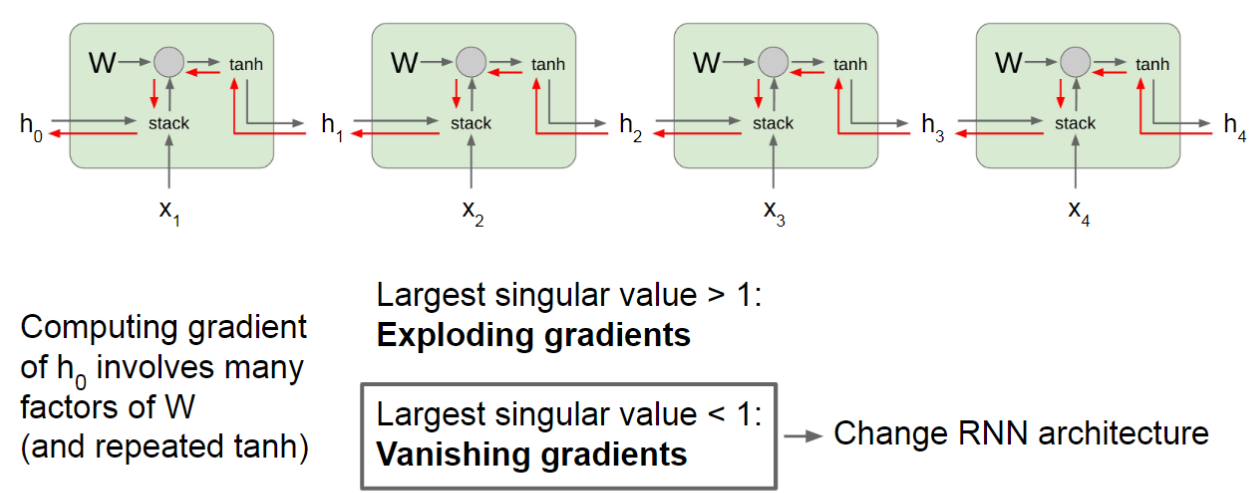
RNN的梯度流向如下图红箭头所示：

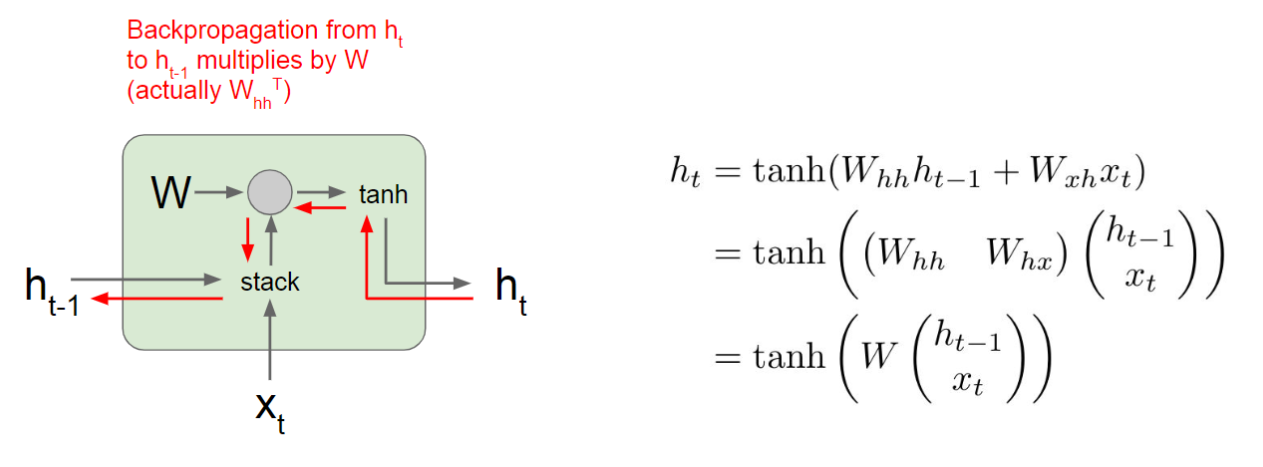
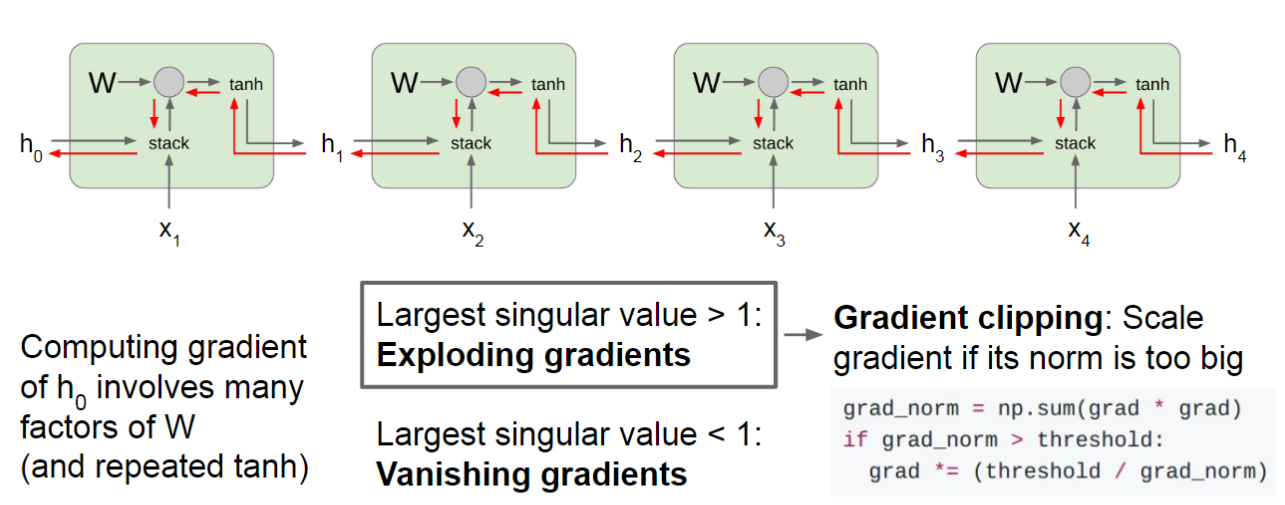
RNN会遇到梯度消失和梯度爆炸的问题。根据前面的公式，\(\delta_{t,k}\)实际上是递归定义的，展开得到：

\[\delta_{t,k}=\prod\limits_{\tau=k}^{t-1}(\text{diag}(f^\prime(z_\tau))U^T)\delta_{t,t}\]

如果定义\(\gamma\cong\parallel\text{diag}(f^\prime(z_\tau))U^T\parallel\)，那么\(\delta_{t,k}\cong\gamma^{t-k}\delta_{t,t}\)。在\(t-k\)很大时，\(\gamma<1\)会导致梯度消失，\(\gamma>1\)时会导致梯度爆炸。

Long Short Time Memory

LSTM是一种解决RNN梯度消失问题的改进版本：

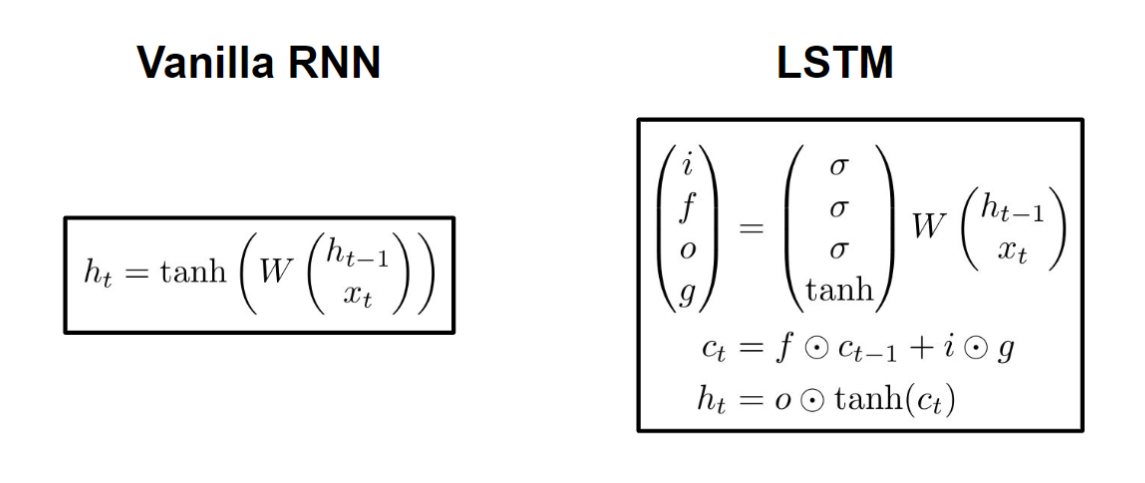
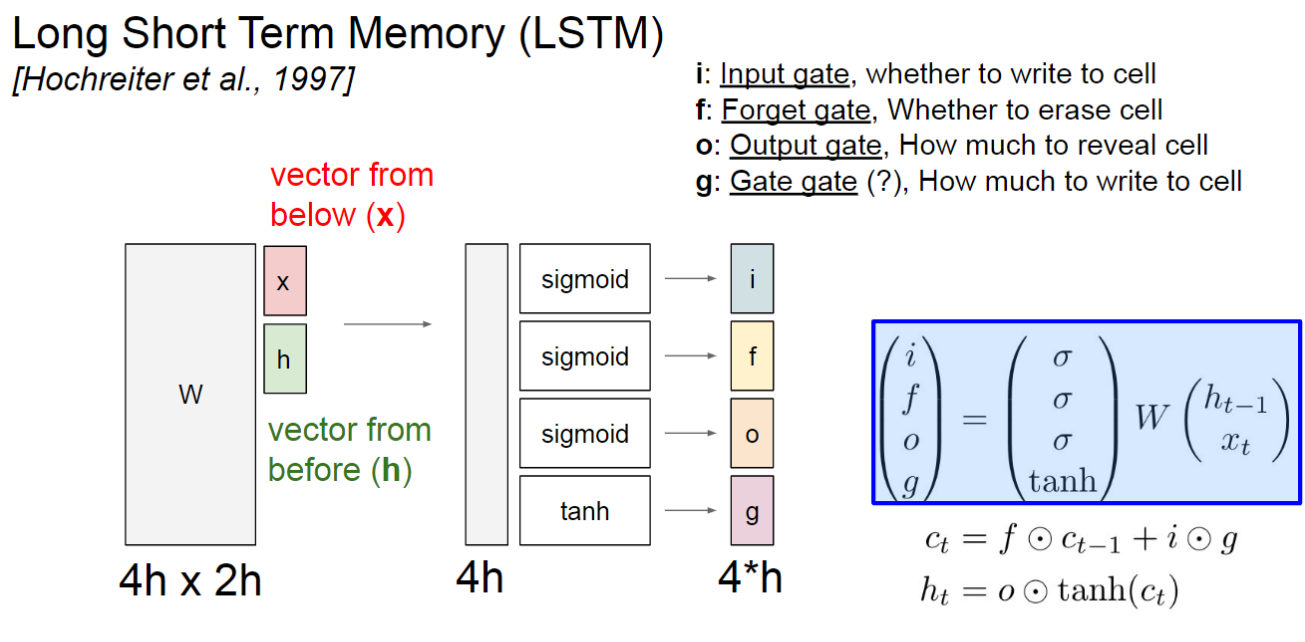
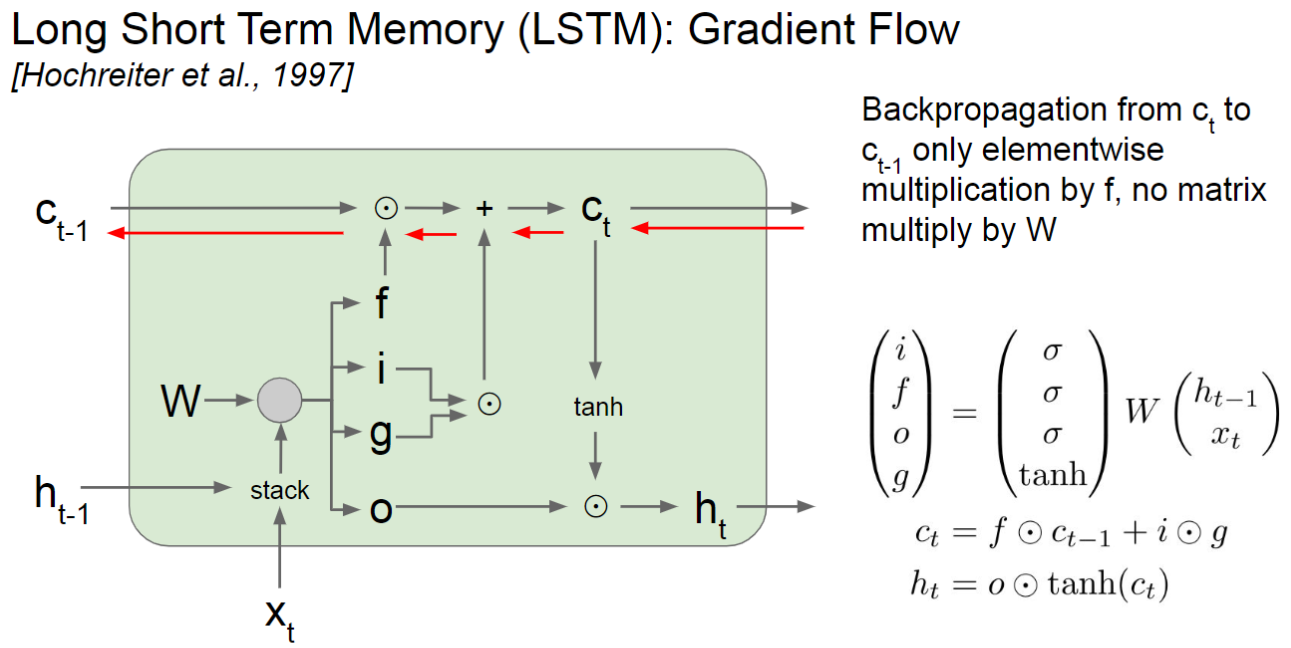
在LSTM中，维护了两个State，\(c_t\)和\(h_t\)。其中\(c_t\)由遗忘门\(f\)与上一个\(c_{t-1}\)相乘(代表继承上一个Cell的信息并加以一定程度的遗忘)，加上输出门\(i\)与Gate Gate \(g\)相乘(Gate Gate代表当前的候选状态，输出门\(i\)控制当前候选状态有多少信息需要保存)。最后，输出门\(o\)控制当前时刻的Cell State \(c_t\)有多少信息需要输出给外部状态\(h_t\)。

三个门的计算方式为：

\[i_t=\sigma(W_ix_t+U_ih_{t-1}+b_i)\]

\[f_t=\sigma(W_fx_t+U_fh_{t-1}+b_f)\]

\[o_t=\sigma(W_ox_t+U_oh_{t-1}+b_o)\]

Methodology

总体框架图如Fig 1所示：

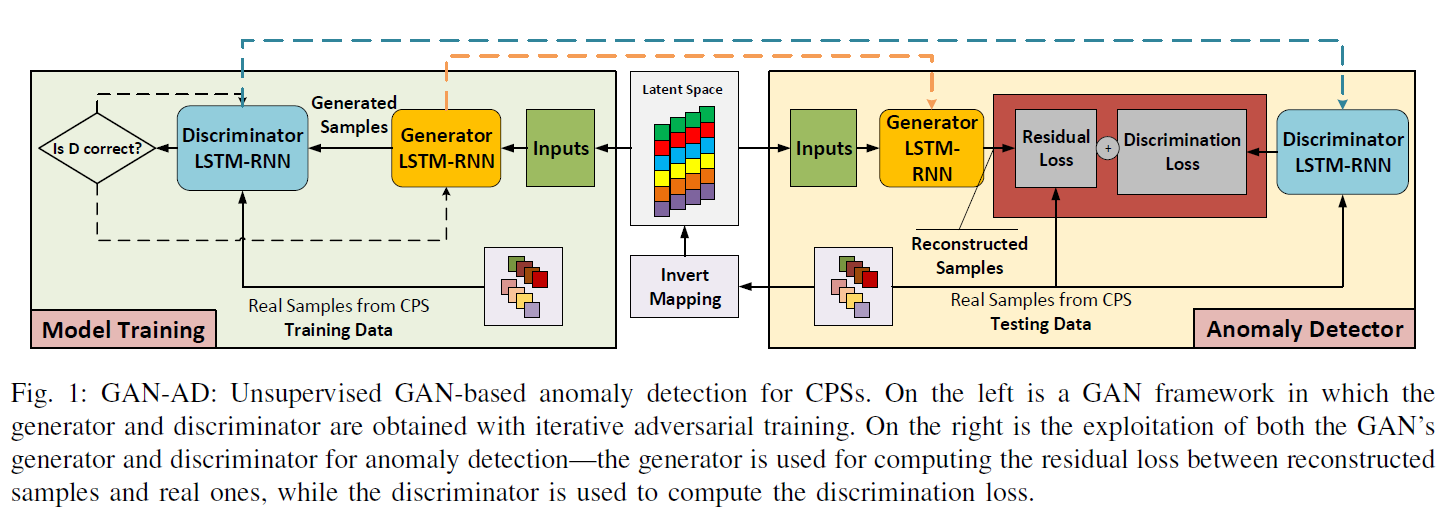
GAN with LSTM-RNN

网络结构上生成器和判别器都是LSTM，优化函数和普通GAN一样：

\[\min\limits_G\max\limits_D V(D,G)=\mathbb{E}_{x\sim p_{data}(x)}[\log D(x)]+\mathbb{E}_{z\sim p_z(z)}[\log (1-D(G(z)))]\]

GAN-based Anomaly Score

在测试阶段，需要使用梯度优化寻找一个使得\(G_{rnn}(z)\)最接近\(X^{test}\)的\(z^k\)：

\[\min\limits_{Z^k}Error(X^{test},G_{rnn}(Z^k))=1-Similarity(X^{test},G_{rnn}(Z^k))\]

本文定义了两种Anomaly Score，一种是Residual Loss：

\[Res(X^{test}_t)=\sum\limits_{i=1}^n|x^{test,i}_t-G_{rnn}(Z^{k,i}_t)|\]

一种是Discrimination Loss，即判别器的输出\(D_{rnn}(x_t^{test})\)。

总的Anomaly Score：

\[S^{test}_t=\lambda Res(X^{test}_t)+(1-\lambda)D_{rnn}(x^{test}_t)\]

Anomaly Detection Framework

模型的算法流程如下：

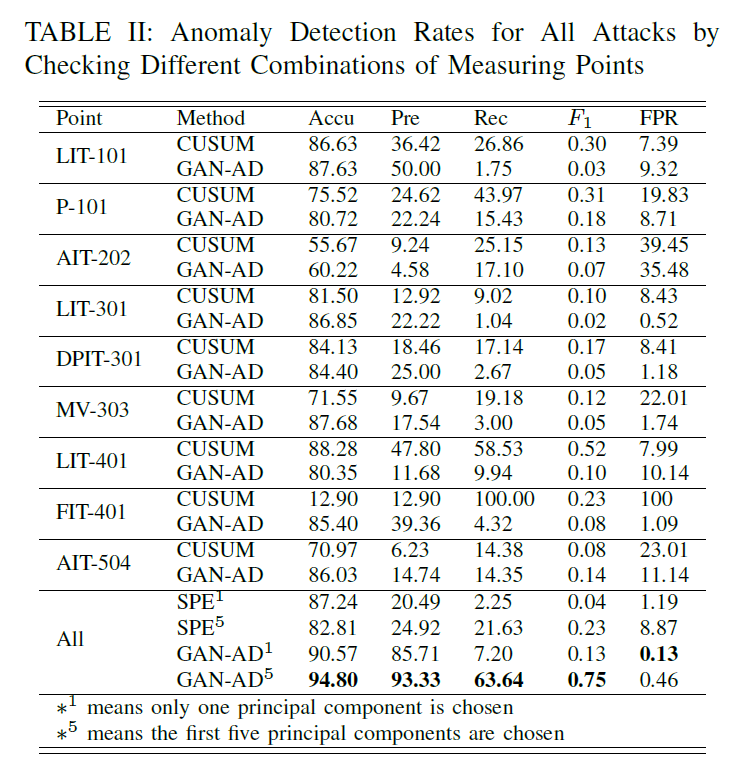
由于本文是多变量时间序列预测，而且时间序列的长度有可能比较长，作者使用了滑动窗口和PCA来进行预处理。

Experiments